Câu hỏi:
18/07/2024 126
Cho hàm số y = f(x) có bảng biến thiên như hình bên.
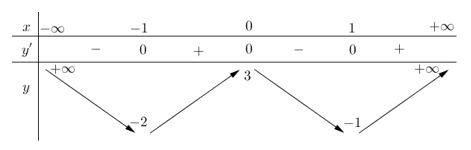
Phương trình có bao nhiêu nghiệm trên
Cho hàm số y = f(x) có bảng biến thiên như hình bên.

Phương trình có bao nhiêu nghiệm trên
A. 3.
B. 4
C. 5
D. 6
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt
Với
Khi đó phương trình trở thành
Dựa vào BBT ta thấy đường thẳng cắt đồ thị hàm số y = f(t) tại 2 điểm phân biệt
Ta có đồ thị hàm số trên như sau:
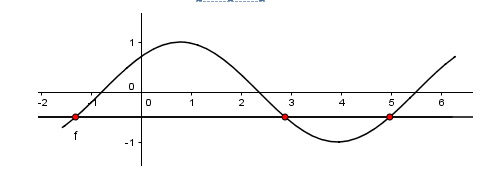
Dựa vào đồ thị ta thấy, phương trình t = a vô nghiệm, phương trình t = b có 3 nghiệm phân biệt.
Chọn A.
Đặt
Với
Khi đó phương trình trở thành
Dựa vào BBT ta thấy đường thẳng cắt đồ thị hàm số y = f(t) tại 2 điểm phân biệt
Ta có đồ thị hàm số trên như sau:

Dựa vào đồ thị ta thấy, phương trình t = a vô nghiệm, phương trình t = b có 3 nghiệm phân biệt.
Chọn A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ:
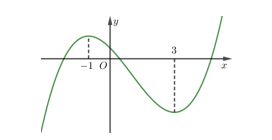
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số có 3 điểm cực trị. Tổng các phần tử của S là:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số có 3 điểm cực trị. Tổng các phần tử của S là:
Câu 2:
Đường cong ở hình bên dưới là đồ thị của hàm số với a, b, c, d là các số thực. Giá trị nhỏ nhất của hàm số trên đoạn [-1; 0] là
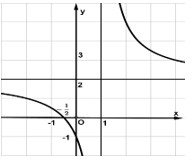
Câu 3:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Thể tích khối tứ diện ABDB' bằng
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Thể tích khối tứ diện ABDB' bằng
Câu 5:
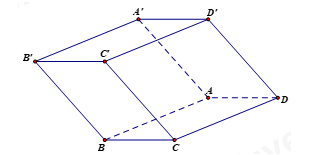
Cho hình lăng trụ ABCD.A'B'C'D' đáy là hình bình hành. Thể tích khối tứ diện BCDA' là
Câu 8:
Trong không gian Oxyz đường thẳng Ox có phương trình nào dưới đây
Trong không gian Oxyz đường thẳng Ox có phương trình nào dưới đây
Câu 9:
Trong không gian Oxyz, gọi A là điểm thuộc mặt cầu tâm I bán kính R. Chọn phương án đúng.
Trong không gian Oxyz, gọi A là điểm thuộc mặt cầu tâm I bán kính R. Chọn phương án đúng.
Câu 10:
Trong không gian Oxyz tọa độ điểm đối xứng của điểm M(0; 1; 2) qua mặt phẳng x + y + z = 0
Trong không gian Oxyz tọa độ điểm đối xứng của điểm M(0; 1; 2) qua mặt phẳng x + y + z = 0
Câu 11:
Cho hình lăng trụ . Số đoạn thẳng có hai đỉnh là đỉnh hình lăng trụ là
Cho hình lăng trụ . Số đoạn thẳng có hai đỉnh là đỉnh hình lăng trụ là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)