Câu hỏi:
23/07/2024 1,027
Cho hàm số f (x) = mx4 + 2(m - 1)x2 với m là tham số thực. Nếu thì bằng
Cho hàm số f (x) = mx4 + 2(m - 1)x2 với m là tham số thực. Nếu thì bằng
A. 2;
A. 2;
B. -1;
B. -1;
C. 4;
D. 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
f '(x) = 4mx3 + 4(m - 1)x
Do f (x) là hàm đa thức và
Thay vào hàm số ban đầu ta được
Þ y' = 2x3 - 2x = 2x(x - 1)(x + 1)
Ta có BBT:
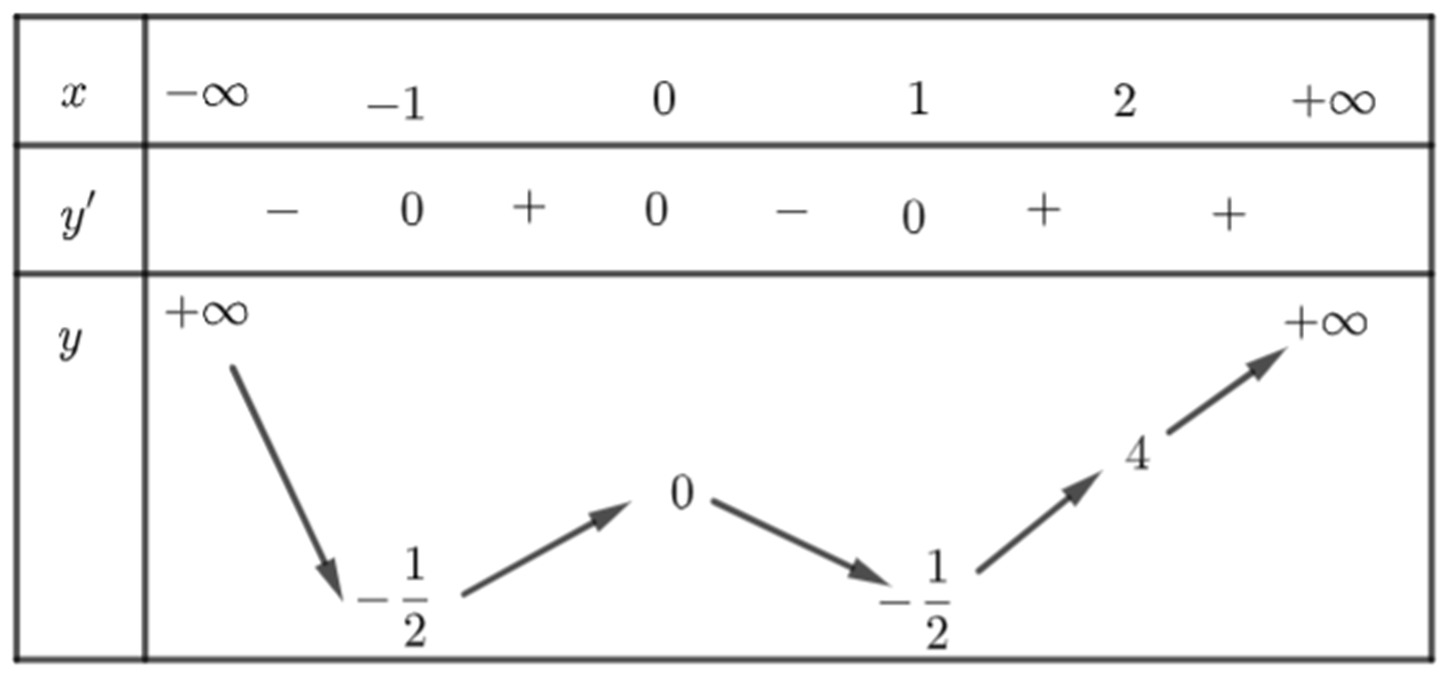
Vậy với , thì .
Dựa vào BBT ta có
Đáp án đúng là: C
f '(x) = 4mx3 + 4(m - 1)x
Do f (x) là hàm đa thức và
Thay vào hàm số ban đầu ta được
Þ y' = 2x3 - 2x = 2x(x - 1)(x + 1)
Ta có BBT:

Vậy với , thì .
Dựa vào BBT ta có
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và . Gọi S là diện tích hình phẳng giới hạn bỡi các đường y = F (x), y = G (x), x = 0 và x = 5. Khi S = 20 thì a bằng?
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và . Gọi S là diện tích hình phẳng giới hạn bỡi các đường y = F (x), y = G (x), x = 0 và x = 5. Khi S = 20 thì a bằng?
Câu 2:
Có bao nhiêu số nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Có bao nhiêu số nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Câu 3:
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (5b - 1)(a.2b - 5) < 0?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (5b - 1)(a.2b - 5) < 0?
Câu 5:
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Câu 6:
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + z + 6 = 0. Khi đó z1 + z2 + z1z2 bằng:
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + z + 6 = 0. Khi đó z1 + z2 + z1z2 bằng:
Câu 7:
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 3z1z2 = 4z3(z1 + z2). Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 3z1z2 = 4z3(z1 + z2). Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Câu 8:
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + 4x - 3y bằng
Xét tất cả các số thực x, y sao cho với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + 4x - 3y bằng
Câu 10:
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
Câu 11:
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 1. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 1. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Câu 13:
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
Câu 14:
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
Câu 15:
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
Trong không gian Oxyz, cho điểm A(1; 2; -3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)