Câu hỏi:
16/07/2024 228Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là các đường cong như hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là B, đồ thị hàm số y = g(x) có đúng một điểm cực trị là A và Có bao nhiêu số nguyên để hàm số có đúng 5 điểm cực trị?
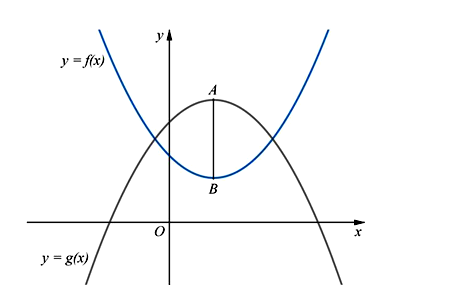
A. 2019
B. 2021
C. 2022
D. 2020
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
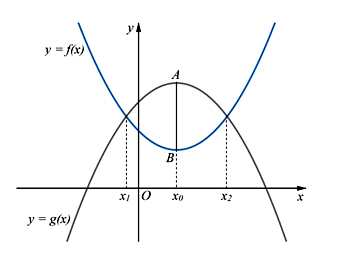
* Đặt
Từ các đồ thị đã cho, ta có:
Bảng biến thiên của h(x) và |h(x)|
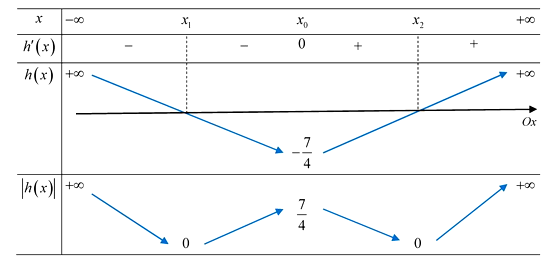
Từ bảng biến thiên, ta thấy: hàm số y = |h(x)| có 3 điểm cực trị.
* Đồ thị hàm số có cùng số điểm cực trị với đồ thị hàm số y = |h(x)|. Do đó, hàm số cũng có 3 điểm cực trị.
* Hàm số có số điểm cực trị bằng số điểm cực trị của hàm số cộng số giao điểm không trùng với các điểm cực trị của đồ thị hàm số với trục Ox.
Vì vậy, để hàm số có đúng 5 điểm cực trị thì đồ thị hàm số và trục Ox phải có 2 giao điểm khác các điểm cực trj hay đường thẳng y = -m phải cắt đồ thị hàm số y = |h(x)| tại 2 điểm phân biệt khác các điểm cực trị.
Từ bảng biến thiên của hàm số y = |h(x)|, điều kiện của m thỏa mãn ycbt là: ,
và
Vậy số giá trị nguyên của m thỏa mãn là: 2019.
Chọn A.

* Đặt
Từ các đồ thị đã cho, ta có:
Bảng biến thiên của h(x) và |h(x)|

Từ bảng biến thiên, ta thấy: hàm số y = |h(x)| có 3 điểm cực trị.
* Đồ thị hàm số có cùng số điểm cực trị với đồ thị hàm số y = |h(x)|. Do đó, hàm số cũng có 3 điểm cực trị.
* Hàm số có số điểm cực trị bằng số điểm cực trị của hàm số cộng số giao điểm không trùng với các điểm cực trị của đồ thị hàm số với trục Ox.
Vì vậy, để hàm số có đúng 5 điểm cực trị thì đồ thị hàm số và trục Ox phải có 2 giao điểm khác các điểm cực trj hay đường thẳng y = -m phải cắt đồ thị hàm số y = |h(x)| tại 2 điểm phân biệt khác các điểm cực trị.
Từ bảng biến thiên của hàm số y = |h(x)|, điều kiện của m thỏa mãn ycbt là: ,
và
Vậy số giá trị nguyên của m thỏa mãn là: 2019.
Chọn A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc bốn biết và đồ thị hàm số y = f'(x) hình vẽ. Hàm số đồng biến trên khoảng
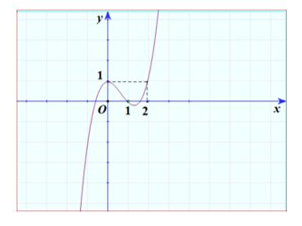

Câu 2:
Cho hình chóp S.ABC có Góc giữa SA và mặt phẳng (SBC) bằng Thể tích khối chóp S.ABC bằng
Cho hình chóp S.ABC có Góc giữa SA và mặt phẳng (SBC) bằng Thể tích khối chóp S.ABC bằng
Câu 3:
Có bao nhiêu số nguyên dương m sao cho ứng với mỗi m luôn có ít hơn 4041 số nguyên x thỏa mãn
Có bao nhiêu số nguyên dương m sao cho ứng với mỗi m luôn có ít hơn 4041 số nguyên x thỏa mãn
Câu 5:
Một khối lập phương có thể tích bằng 27 thì độ dài cạnh của hình lập phương đó bằng
Một khối lập phương có thể tích bằng 27 thì độ dài cạnh của hình lập phương đó bằng
Câu 6:
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng 2022. Khoảng cách từ điểm A đến mặt phẳng (BCC'B') bằng
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng 2022. Khoảng cách từ điểm A đến mặt phẳng (BCC'B') bằng
Câu 7:
Diện tích xung quanh của hình nón có bán kính đáy r = 5cm và độ dài đường sinh l = 4cm bằng
Diện tích xung quanh của hình nón có bán kính đáy r = 5cm và độ dài đường sinh l = 4cm bằng
Câu 10:
Cho hàm số f(x) có đạo hàm cấp 2 liên tục trên thỏa mãn số nguyên x thỏa mãn Tính
Cho hàm số f(x) có đạo hàm cấp 2 liên tục trên thỏa mãn số nguyên x thỏa mãn Tính
Câu 11:
Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là
Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là
Câu 13:
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, tam giác ABD đều cạnh bằng và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SO và mặt phẳng (ABCD) bằng
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, tam giác ABD đều cạnh bằng và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SO và mặt phẳng (ABCD) bằng
Câu 14:
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0; 3]. Hiệu M - m bằng
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0; 3]. Hiệu M - m bằng
Câu 15:
Chọn ngẫu nhiên một số trong 17 số nguyên dương đầu tiên. Xác suất để chọn được số nguyên tố bằng
Chọn ngẫu nhiên một số trong 17 số nguyên dương đầu tiên. Xác suất để chọn được số nguyên tố bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)