Câu hỏi:
23/07/2024 253
Cho ∆ABC có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = CF và AG cắt BC tại E. Số đo là :
Cho ∆ABC có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = CF và AG cắt BC tại E. Số đo là :
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
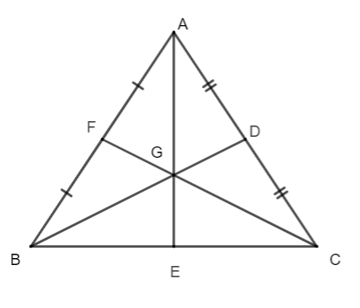
Xét ∆ABC có:
BE là đường trung tuyến (E là trung điểm của AC);
CF là đường trung tuyến (F là trung điểm của AB);
BE và CF cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra AE là đường trung tuyến của ∆ABC.
Do vậy E là trung điểm của BC.
Ta có: ; (G là trọng tâm ∆ABC).
mà BD = CF (gt) nên BG = CG.
Do vậy FG = GD.
Xét ∆FGB và ∆DGC có:
BG = CG (cmt);
FG = GD (cmt);
= ( hai góc đối đỉnh).
Do đó ∆FGB = ∆DGC (c.g.c).
Suy ra BF = DC (hai cạnh tương ứng).
Ta có : AB = BF (F là trung điểm của AB);
AC= DC (D là trung điểm của AC);
BF = DC (cmt).
Do đó AB = AC.
Xét ∆AEB và ∆AEC ta có:
AB = AC (cmt);
AE là cạnh chung;
EB = EC (E là trung điểm của BC).
Do đó ∆AEB = ∆AEC (c.c.c).
Suy ra = 90°.
Hướng dẫn giải
Đáp án đúng là: D

Xét ∆ABC có:
BE là đường trung tuyến (E là trung điểm của AC);
CF là đường trung tuyến (F là trung điểm của AB);
BE và CF cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra AE là đường trung tuyến của ∆ABC.
Do vậy E là trung điểm của BC.
Ta có: ; (G là trọng tâm ∆ABC).
mà BD = CF (gt) nên BG = CG.
Do vậy FG = GD.
Xét ∆FGB và ∆DGC có:
BG = CG (cmt);
FG = GD (cmt);
= ( hai góc đối đỉnh).
Do đó ∆FGB = ∆DGC (c.g.c).
Suy ra BF = DC (hai cạnh tương ứng).
Ta có : AB = BF (F là trung điểm của AB);
AC= DC (D là trung điểm của AC);
BF = DC (cmt).
Do đó AB = AC.
Xét ∆AEB và ∆AEC ta có:
AB = AC (cmt);
AE là cạnh chung;
EB = EC (E là trung điểm của BC).
Do đó ∆AEB = ∆AEC (c.c.c).
Suy ra = 90°.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là:
Cho tam giác ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là:
Câu 2:
Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:
Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:
Câu 3:
Điền vào chỗ trống sau: “Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua điểm ấy.”
Điền vào chỗ trống sau: “Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua điểm ấy.”
Câu 4:
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
Câu 5:
Cho tam giác ∆ABC cân tại A có hai điểm E và F lần lượt là trung điểm của AC và AB. Khi đó tam giác GBC là:
Cho tam giác ∆ABC cân tại A có hai điểm E và F lần lượt là trung điểm của AC và AB. Khi đó tam giác GBC là:
Câu 6:
Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = 9 cm. Độ dài đoạn thẳng GF bằng:
Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = 9 cm. Độ dài đoạn thẳng GF bằng:
Câu 8:
Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:
Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:
Câu 9:
Cho hình vẽ như bên dưới. Biết AM = 12 cm. Tính chiều dài của đoạn thẳng AG.
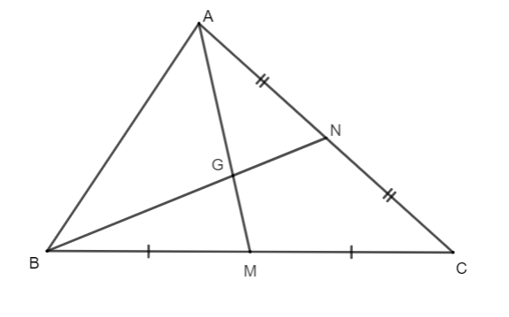
Cho hình vẽ như bên dưới. Biết AM = 12 cm. Tính chiều dài của đoạn thẳng AG.

Câu 10:
Cho hình vẽ như bên dưới. Biết GN = 4 cm. Độ dài đoạn thẳng BN bằng:
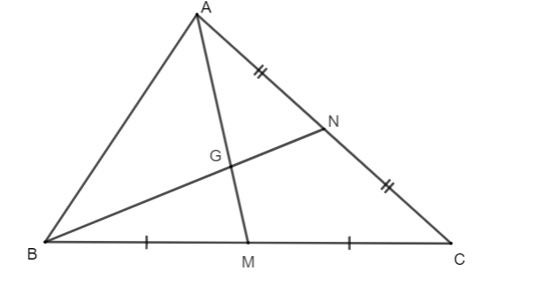

Câu 11:
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
Câu 12:
Điền vào chỗ trống sau: “Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với ... của cạnh đối diện”.
Điền vào chỗ trống sau: “Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với ... của cạnh đối diện”.
Câu 14:
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng:
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng: