Cho a, b là hai số thực dương. Tìm số điểm cực trị của hàm số $y=|x^4-a{x}^2-b|.$

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y - 3z + 5 = 0. Véc tơ nào sau đây là véc tơ pháp tuyến của mặt phẳng (P)?

Từ các chữ số 1, 2, 3, 4 ta có thể tạo thành bao nhiêu số tự nhiên gồm 6 chữ số, trong đó chữ số 1 xuất hiện đúng 3 lần, ba chữ số 2, 3, 4 hiện diện đúng 1 lần.

Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=x^3-3x^2$ trên đoạn $[-2;1].$ Tính giá trị của $T=M+m.$

Gọi n, d lần lượt là số tiệm cận ngang, tiệm cận đứng của đồ thị hàm số $y=\frac{x-1}{\sqrt{2x^2-1}-1}$ Mệnh đề nào sau đây đúng?

Từ một hộp chứa 5 quả cầu trắng, 3 quả cầu đỏ và 2 quả cầu xanh. Lấy ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để lấy được 2 quả không trắng.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = 2a, $\widehat{SAB}=\widehat{SCB}=90°$ và góc giữa đường thẳng AB và mặt phẳng (SBC) bằng $30°$. Tính thể tích V của khối chóp đã cho.

Cho hình phẳng H được giới hạn bởi các đường thẳng  Tính thể tích V của vật thể tròn xoay khi quay quanh hình phẳng H quanh trục hoành.

Biết rằng ${\int }_1^2\ln (x+1)dx=a\ln 3+b\ln 2+c$ với a, b, c là các số nguyên. Tính S = a +b + c.

Tìm tất cả các giá trị thực của tham số m để bất phương trình $2^{3x}+\left(m-1\right)3^x+m-1>0$ nghiệm đúng $\forall x\in \mathrm{ℝ}$.

Cho tứ diện ABCD có $AD\perp \left(ABC\right)$, đáy ABC thỏa mãn điều kiện $\frac{cot A+cot B+cot C}{2}$=$\frac{BC}{AB.AC}+\frac{CA}{BC.BA}+\frac{AB}{CA.CB}.$ Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC. Tính thể tích V của khối cầu ngoại tiếp khối chóp A.BCHK

Tìm tất các giá trị thực của tham số m để hàm số $y=\ln \left(x+\sqrt{x^2+1}\right)-mx$ có cực trị.

Tìm các hàm số f(x) biết $f\text{'}\left(x\right)=\frac{\cos x}{{\left(2+\sin x\right)}^2}$

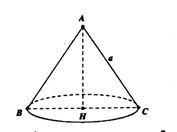
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh $S_{xq}$của hình nón đó.

Tìm tất cả các khoảng đồng biến của hàm số $y=\frac{x}{x^2+1}$

Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất. Tổng của góc lớn nhất và góc bé nhất bằng: