Câu hỏi:
22/07/2024 873
Cho tứ giác ABCD có AC và BD giao nhau tại O và một điểm S không thuộc mặt phẳng . Trên đoạn SC lấy một điểm M không trùng với S và C. Giao điểm của đường thẳng SD với mặt phẳng là
A. giao điểm của SD và AB
B. giao điểm của SD và AM
C. giao điểm của SD và BK (với )
D. giao điểm của SD và MK (với )
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
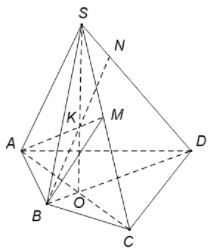
● Chọn mặt phẳng phụ chứa SD.
● Tìm giao tuyến của hai mặt phẳng và .
Ta có là điểm chung thứ nhất của và .
Trong mặt phẳng , gọi . Trong mặt phẳng , gọi . Ta có:
+ ABCD mà 2a suy ra M.
+ N mà AC suy ra BC.
Suy ra P là điểm chung thứ hai của BCD và .
Do đó .
● Trong mặt phẳng , gọi Ta có:
+ mà BCD suy ra P.
+ N.
Vậy BC.
Chọn C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng là
Câu 2:
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng và là:
Câu 3:
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a. Gọi M, N lần lượt là trung điểm các cạnh AC, BC; P là trọng tâm tam giác BCD. Mặt phẳng cắt tứ diện theo một thiết diện có diện tích là:
Câu 4:
Cho điểm A không nằm trên mặt phẳng chứa tam giác BCD. Lấy E, F là các điểm lần lượt nằm trên các cạnh AB, AC. Khi EF và BC cắt nhau tại I, thì I không phải là điểm chung của hai mặt phẳng nào sau đây?
Câu 5:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Mặt phẳng qua MN cắt AD, BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
Câu 7:
Cho tứ diện ABCD. Gọi H, K lần lượt là trung điểm các cạnh AB, BC. Trên đường thẳng CD lấy điểm M nằm ngoài đoạn CD. Thiết diện của tứ diện với mặt phẳng là:
Câu 8:
Cho bốn điểm N không cùng ở trong một mặt phẳng. Gọi P lần lượt là trung điểm của D. Trên MND lấy điểm MND sao cho không song song với (không trùng với các đầu mút). Gọi E là giao điểm của đường thẳng D với mặt phẳng H. Mệnh đề nào sau đây đúng?


