Câu hỏi:
22/07/2024 388
b) Xác định đoạn vuông góc chung của AB và CD.
b) Xác định đoạn vuông góc chung của AB và CD.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
b) Gọi H là hình chiếu vuông góc M của trên CD.
Ta có {(CMD)⊥ABCD⊥MH⇒{MH⊥ABCD⊥MH
Do đó MH là đoạn vuông góc chung của AB và CD.
b) Gọi H là hình chiếu vuông góc M của trên CD.
Ta có {(CMD)⊥ABCD⊥MH⇒{MH⊥ABCD⊥MH
Do đó MH là đoạn vuông góc chung của AB và CD.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho tứ diện OABC có ba cạnh OA, OB, OC đều bằng a và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng:
a) OA và BC;
Cho tứ diện OABC có ba cạnh OA, OB, OC đều bằng a và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng:
a) OA và BC;
Câu 4:
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.
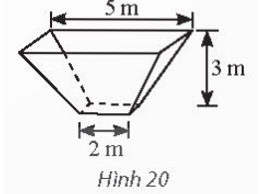
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.

Câu 5:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng AC và SB.
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng AC và SB.
Câu 6:
Cho hình hộp đứng ABCD.A′B′C′D′ có cạnh bên AA′ = 2a và đáy ABCD là hình thoi có AB = a và AC=a√3.
a) Tính khoảng cách giữa hai đường thẳng BD và AA′.
Cho hình hộp đứng ABCD.A′B′C′D′ có cạnh bên AA′ = 2a và đáy ABCD là hình thoi có AB = a và AC=a√3.
a) Tính khoảng cách giữa hai đường thẳng BD và AA′.
Câu 7:
Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng AB ⊥ CD.
Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng AB ⊥ CD.
Câu 8:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết SA = a và SA ⊥ (ABCD). Cho biết OA = a.
a) Tính khoảng cách từ B đến (SAD).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết SA = a và SA ⊥ (ABCD). Cho biết OA = a.
a) Tính khoảng cách từ B đến (SAD).
Câu 9:
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.
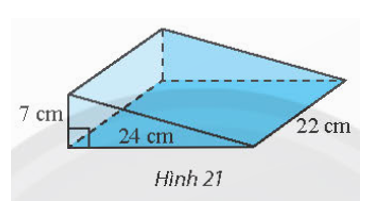
Câu 10:
Tính thể tích của khối chóp cụt lục giác đều ABCDEF.A′B′C′D′E′F′ với O và O′ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và a2,OO'.
Tính thể tích của khối chóp cụt lục giác đều ABCDEF.A′B′C′D′E′F′ với O và O′ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và a2,OO'.
Câu 11:
Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng a nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi b là đường thẳng kẻ theo tim đường. Tính khoảng cách giữa hai đường thẳng a và b.

Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng a nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi b là đường thẳng kẻ theo tim đường. Tính khoảng cách giữa hai đường thẳng a và b.

Câu 12:
Một căn phòng có trần cao 3,2 m. Tính khoảng cách giữa một đường thẳng a trên trần nhà và đường thẳng b trên sàn nhà.
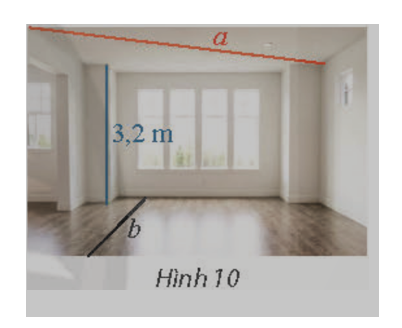
Một căn phòng có trần cao 3,2 m. Tính khoảng cách giữa một đường thẳng a trên trần nhà và đường thẳng b trên sàn nhà.

Câu 13:
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách :
a) Giữa hai mặt phẳng (ACD′) và (A′C′B) ;
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách :
a) Giữa hai mặt phẳng (ACD′) và (A′C′B) ;
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có O là giao điểm của hai đường chéo, . Tính khoảng cách từ O đến mặt phẳng (SCD).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có O là giao điểm của hai đường chéo, . Tính khoảng cách từ O đến mặt phẳng (SCD).
Câu 15:
a) Cho điểm M và đường thẳng a không đi qua M. Trong mặt phẳng (M; a) dùng êke để tìm H trên a sao cho MH ⊥ a (Hình 1a) . Đo độ dài đoạn MH.
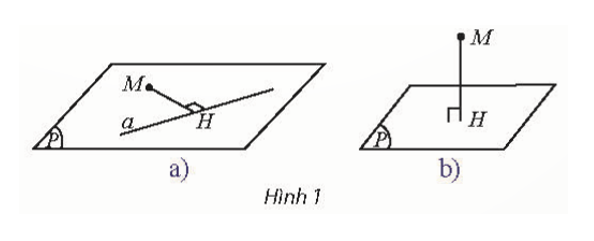
a) Cho điểm M và đường thẳng a không đi qua M. Trong mặt phẳng (M; a) dùng êke để tìm H trên a sao cho MH ⊥ a (Hình 1a) . Đo độ dài đoạn MH.



