TOP 15 câu Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (Cánh diều 2024) có đáp án - Toán 7
Bộ 15 câu hỏi trắc nghiệm Toán lớp 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc có đáp án đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 6.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 7 Cánh diều bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 033000255833 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc - Cánh diều
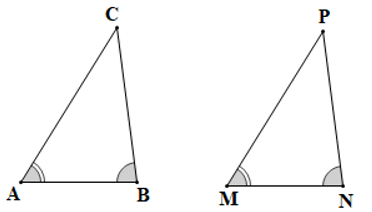
Câu 1. Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét ∆ABC và ∆MNP có:
.............,
BC = PN.
;
Vậy ΔABC = ∆MNP (g.c.g)”
A. AB = MN;
B.
C. AC = MP;
D.
Đáp án đúng là: B
Ta có: ΔABC = ∆MNP theo trường hợp góc – cạnh – góc nên hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.
Mà BC = PN và nên cặp góc kề tương ứng còn lại là
Vậy ta chọn phương án B.
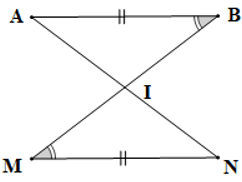
Câu 2. Cho hình vẽ sau:
Khẳng định nào sau đây là đúng ?
A. ΔAIB = ΔMIN;
B. ΔAIB = ΔMNI;
C. ΔAIB = ΔIMN;
D. ΔAIB = ΔNIM.
Đáp án đúng là: D
Vì mà hai góc này ở vị trí so le trong
Nên AB // MN (dấu hiệu nhận biết)
Suy ra (hai góc so le trong)
Xét ΔABI và ΔIMN có:
(chứng minh trên),
AB = MN (giả thiết),
(giả thiết)
Do đó ΔAIB = ΔNIM (g.c.g)
Vậy ta chọn phương án D.
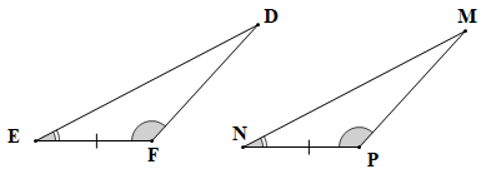
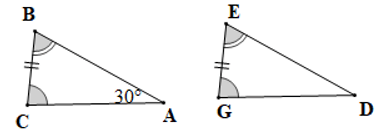
Câu 3. Cho tam giác FDE và tam giác MNP có , FE = NP. Biết , số đo góc M là:
A. 50°;
B. 45°;
C. 25°;
D. 30°.
Đáp án đúng là: C
Xét ΔFDE và ΔMNP có:
(giả thiết),
FE = NP (giả thiết),
(giả thiết),
Do đó ΔFDE và ΔPMN (g.c.g)
Suy ra (hai góc tương ứng)
Ta lại có: (tổng ba góc trong tam giác FDE)
Suy ra
Mà nên .
Vậy .
Câu 4. Cho hình vẽ dưới đây:
Độ dài đoạn thẳng CA bằng:
A. 2 cm;
B. 3 cm;
C. 4 cm;
D. 5 cm.
Đáp án đúng là: A
Xét ∆ABO và ∆ACO có:
(giả thiết),
AO là cạnh chung,
(giả thiết)
Do đó ∆ABO = ∆ACO (g.c.g)
Suy ra AB = AC (hai cạnh tương ứng)
Mà BA = 2 cm, do đó AC = 2 cm.
Vậy ta chọn phương án A.
Câu 5. Cho ΔABC và ΔMNP có . Để ΔABC = ΔMNP theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
A. AB = MN;
B. AC = MP;
C. BC = NP;
D. .
Đáp án đúng là: A
Để ΔABC = ΔMNP theo trường hợp góc – cạnh – góc mà nên điều kiện còn thiếu là điều kiện về cạnh, sao cho hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh này, đó là AB = MN.
Vậy ta chọn phương án A.
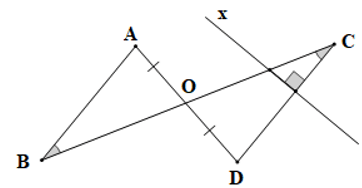
Câu 6. Cho hình vẽ dưới đây:
Xét các khẳng định:
(1) BA = CD;
(2) x BA.
Chọn câu đúng:
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
Đáp án đúng là: C
Ta có: mà hai góc này ở vị trí so le trong nên AB // CD (dấu hiệu nhận biết)
Do đó (hai góc so le trong)
Xét ΔABO và ΔDCO có:
(chứng minh trên),
AO = OD (giả thiết),
(hai góc đối đỉnh)
Do đó ΔABO = ΔDCO (g.c.g)
Suy ra AB = CD (hai cạnh tương ứng)
Khi đó (1) đúng.
Ta lại có AB // CD (chứng minh trên) mà x CD (giả thiết)
Do đó x AB. Nên (2) đúng.
Vậy cả (1) và (2) đều đúng, ta chọn phương án C.
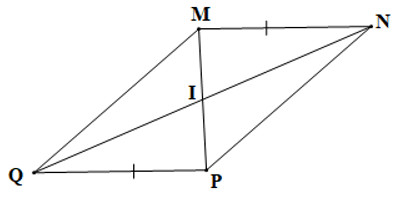
Câu 7. Cho tứ giác MNPQ, MN // PQ, MN = PQ, I là giao điểm của MP và NQ. Cho các khẳng định sau:
(1) MQ = NP;
(2) IM = IP;
(3) IN = IQ.
Số khẳng định sai là:
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án đúng là: A
Vì MN // PQ (giả thiết)
Nên và (các cặp góc so le trong)
• Xét ΔMIN và ΔPIQ có:
(do ),
MN = PQ (giả thiết),
(do)
Do đó ΔMIN = ΔPIQ (g.c.g)
Suy ra IM = IP và IN = IQ (các cặp cạnh tương ứng).
Do đó (2) và (3) đều đúng.
• Xét ΔMIQ và ΔPIN có:
IM = IP (chứng minh trên),
(hai góc đối đỉnh),
IN = IQ (chứng minh trên)
Do đó ΔMIQ = ΔPIN (c.g.c)
Suy ra MQ = NP (hai cạnh tương ứng).
Do đó (1) là đúng.
Trong 3 khẳng định không có khẳng định nào sai.
Vậy ta chọn phương án A.
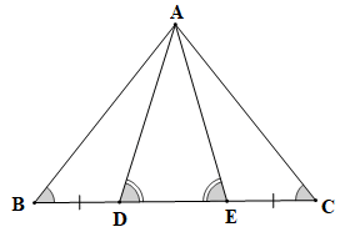
Câu 8. Cho hình vẽ sau:
Cho các khẳng định sau:
(I) ΔABD = ΔACE;
(II) ΔABE = ΔACD;
Khẳng định đúng là:
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I) và (II) đều sai.
D. Cả (I) và (II) đều đúng.
Đáp án đúng là: D.
•Ta có BD = CE (giả thiết)
Nên BD + DE = CE + DE
Suy ra BE = CD
Xét ΔABE và ΔACD có:
(chứng minh trên),
BE = CD (chứng minh trên),
(giả thiết)
Do đó ΔABE = ΔACD (g.c.g).
Vậy (I) đúng.
• Vì ΔABE = ΔACD (chứng minh trên)
Suy ra AB = AC
Xét ΔABD và ΔACE có:
AB = AC (chứng minh trên),
(giả thiết),
BD = CE (giả thiết),
Do đó ΔABD = ΔACE (c.g.c)
Vậy (II) đúng.
Ta chọn phương án C.
Câu 9. Cho tam giác ABC và DEG có , BC = EG. Biết , số đo góc D là:
A. 25°;
B. 30°;
C. 50°;
D. 60°.
Đáp án đúng là: B
Xét ΔABC và ΔGDE có:
(giả thiết),
BC = EG (giả thiết),
(giả thiết),
Do đó ΔABC = ΔDEG (g.c.g)
Suy ra (hai góc tương ứng)
Mà (giả thiết), do đó .
Vậy ta chọn phương án B.
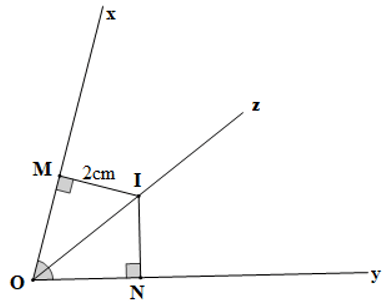
Câu 10. Cho góc xOy, Oz là tia phân giác của góc đó. Gọi I là một điểm trên tia Oz (I khác O). Kẻ IM vuông góc với Ox (M ∈ Ox), IN vuông góc với Oy (N ∈ Oy). Biết độ dài đoạn thẳng IM là 2 cm, độ dài đoạn thẳng IN là:
A. 2 cm;
B. 3 cm;
C. 4 cm;
D. 5 cm.
Đáp án đúng là: A
Xét ΔOIM và ΔOIN có:
(do Oz là tia phân giác của ),
OI là cạnh chung,
Do đó ΔOMI = ΔONI (cạnh huyền – góc nhọn)
Suy ra IM = IN (hai cạnh tương ứng)
Mà IM = 2 cm (giả thiết)
Nên IN = 2 cm
Vậy độ dài đoạn thẳng IN là 2 cm.
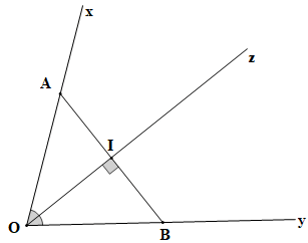
Câu 11. Cho góc xOy nhọn. Trên tia phân giác của góc xOy lấy điểm I tuỳ ý, qua I vẽ đường thẳng vuông góc với OI, cắt Ox ở A và cắt Oy ở B. Khẳng định nào sau đây là đúng?
A. ;
B. IA = IB;
C. OA = OB;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Xét ΔOIA và ΔOIB có:
,
(do OI là tia phân giác của ),
OI là cạnh chung,
Do đó ΔOIA = ΔOIB (cạnh góc vuông – góc nhọn kề)
Suy ra:
• OA = OB, IA = IB (các cặp cạnh tương ứng)
• (hai góc tương ứng)
Vậy ta chọn phương án D.
Câu 12. Cho hình vẽ sau:
Biết CH = 3,5 cm. Số đo cạnh DK là:
A. 2,5 cm;
B. 3,5 cm;
C. 4 cm;
D. 4,5 cm.
Đáp án đúng là: B
Ta có:
• (hai góc kề bù);
• (hai góc kề bù)
Mà (giả thiết) nên
Vì ΔAHC vuông tại A nên (trong tam giác vuông, hai góc nhọn phụ nhau)
Vì ΔBKD vuông tại B nên (trong tam giác vuông, hai góc nhọn phụ nhau)
Mà (chứng minh trên) nên
Xét ΔAHC và ΔBKD có:
(= 90°)
(chứng minh trên),
AC = BD (giả thiết),
Do đó ΔAHC = ΔBKD (cạnh góc vuông – góc nhọn kề)
Suy ra CH = DK (hai cạnh tương ứng)
Mà CH = 3,5 cm nên DK = 3,5 cm.
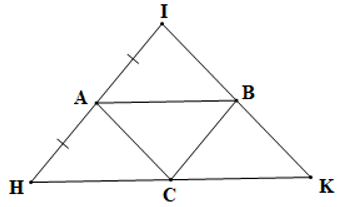
Câu 13. Cho tam giác HIK, A là trung điểm của IH. Đường thẳng qua A và song song với HK cắt IK tại B. Đường thẳng qua B và song song với IH cắt HK tại C. Khẳng định nào sau đây là đúng nhất ?
A. CH = KC;
B. ΔABI = ΔCKB;
C. AI = BC;
D. Cả A, B , C đều đúng.
Đáp án đúng là: D
• Vì AB // HK (giả thiết) nên (hai góc so le trong)
Vì BC // IH (giả thiết) nên (hai góc so le trong)
• Xét ΔABC và ΔCHA có:
(chứng minh trên),
AC là cạnh chung,
(chứng minh trên)
Do đó ΔABC = ΔCHA (g.c.g)
Suy ra BC = AH (hai cạnh tương ứng)
Mà AH = AI (do A là trung điểm của IH)
Do đó BC = AI nên đáp án C là đúng.
• Vì CH // AB (giả thiết) nên (hai góc đồng vị)
Vì IH // CB (giả thiết) nên và (các cặp góc đồng vị)
Do đó
Xét ΔABI và ΔCKB có:
(chứng minh trên),
AI = BC (chứng minh trên),
(chứng minh trên),
Do đó ΔABI = ΔCKB (g.c.g) nên đáp án B là đúng
Suy ra AB = KC (hai cạnh tương ứng)
Mà ΔABC = ΔCHA (chứng minh trên)
Nên AB = CH (hai cạnh tương ứng)
Do đó CH = CK (= AB) nên đáp án A là đúng
Vậy ta chọn đáp án D.
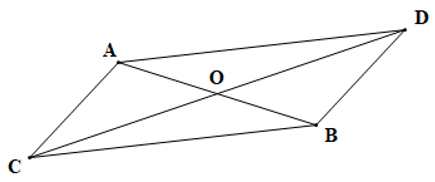
Câu 14. Cho tam giác ABC nhọn. Qua A kẻ đường thẳng song song với BC, qua B kẻ đường thẳng song song với AC, hai đường thẳng này cắt nhau tại D. Giao điểm của AB với CD là O. Khẳng định nào sau đây là sai:
A. ΔABD = ΔBAC;
B. ΔAOD = ΔBOC;
C.
D.
Đáp án đúng là: C
• Vì AD // BC nên , (hai góc so le trong).
Do đó C là sai.
• Vì DB // AC nên (hai góc so le trong).
Do đó D là đúng.
• Xét ΔABD và ΔBAC có:
(chứng minh trên),
AB là cạnh chung,
(chứng minh trên)
Do đó ΔABD = ΔBAC (g.c.g).
Do đó A là đúng.
• Vì ΔABD = ΔBAC (chứng minh trên)
Suy ra AD = BC (hai cạnh tương ứng)
Xét ΔAOD và ΔBOC có:
(vì ),
AD = BC (chứng minh trên),
(vì )
Do đó ΔAOD = ΔBOC (g.c.g).
Do đó B là đúng.
Vậy ta chọn phương án C.
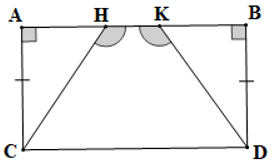
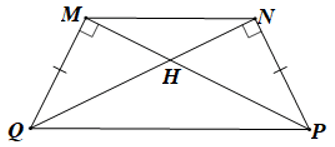
Câu 15. Cho hình thang cân MNPQ như hình vẽ sau:
Trong hình bên có mấy cặp tam giác vuông bằng nhau?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án đúng là: C
Xét ∆MPQ và ∆NQP, có:
,
MQ = NP (do MNPQ là hình thang cân),
PQ là cạnh chung,
Do đó ∆MPQ = ∆NQP (cạnh huyền – cạnh góc vuông).
∆MQH vuông tại M: (1).
∆NPH vuông tại N: (2).
Mà (2 góc đối đỉnh) (3).
Từ (1), (2), (3), ta suy ra .
Xét ∆MQH và ∆NPH, có:
,
MQ = NP (giả thiết),
(chứng minh trên).
Do đó ∆MQH = ∆NPH (cạnh góc vuông – góc nhọn kề).
Vậy ta có 2 cặp tam giác vuông bằng nhau là:
+ ∆MPQ = ∆NQP (cạnh huyền – cạnh góc vuông).
+ ∆MQH = ∆NPH (cạnh góc vuông – góc nhọn kề).
Ta chọn phương án C.
Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác:
Trắc nghiệm Toán 7 Bài 8: Đường vuông góc và đường xiên
Trắc nghiệm Toán 7 Bài 9: Đường trung trực của một đoạn thẳng
Trắc nghiệm Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác
Trắc nghiệm Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác
Trắc nghiệm Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác
Xem thêm các chương trình khác: