TOP 15 câu Trắc nghiệm Tam giác cân (Cánh diều 2024) có đáp án - Toán 7
Bộ 15 câu hỏi trắc nghiệm Toán lớp 7 Bài 7: Tam giác cân có đáp án đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 7.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 7 Cánh diều bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 033000255833 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 7 Bài 7: Tam giác cân - Cánh diều
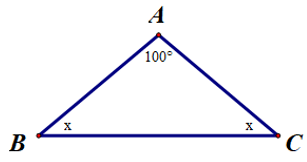
Câu 1. Cho ∆ABC như hình bên. Tìm số đo x:
A. x = 100°;
B. x = 80°;
C. x = 90°;
D. x = 40°.
Đáp án đúng là: D
∆ABC có .
Suy ra ∆ABC cân tại A (dấu hiệu nhận biết)
∆ABC có: (định lí tổng ba góc trong tam giác)
Suy ra 100° + x + x = 180°.
Do đó 2x = 180° – 100° = 80°.
Khi đó ta có x = 80° : 2 = 40°.
Vậy x = 40°.
Ta chọn đáp án D.
Câu 2. Khẳng định nào sau đây sai?
A. Tam giác cân có một góc bằng 60° là tam giác đều;
B. Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân;
C. Trong một tam giác cân, hai góc ở đáy bằng nhau;
D. Tam giác cân không thể là tam giác tù.
Đáp án đúng là: D
Đáp án A, B, C đúng.
Đáp án D:
Tam giác tù là tam giác có một góc bất kỳ lớn hơn 90°.
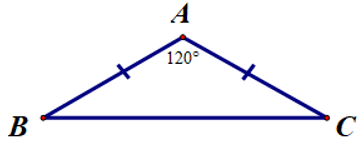
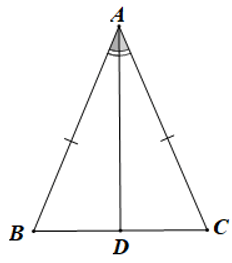
Giả sử ∆ABC cân tại A có (như hình bên).
Vì ∆ABC cân tại A nên ta có (tính chất tam giác cân)
∆ABC có: (định lí tổng ba góc trong tam giác)
Suy ra .
Do đó .
Khi đó .
Do đó ta có .
Ta thấy ∆ABC cân tại A có số đo các cạnh và các góc đều dương.
Mà .
Nên tam giác tù vẫn có thể là tam giác cân.
Do đó đáp án D sai.
Vậy ta chọn đáp án D.
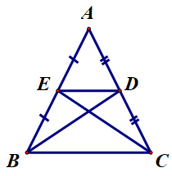
Câu 3. Cho tam giác ABC cân đỉnh A có các đường trung tuyến BD, CE. Tam giác nào dưới đây là tam giác cân?
A. ∆ABD;
B. ∆BCE;
C. ∆ADE;
D. ∆BDE.
Đáp án đúng là: C
∆ABC có BD là đường trung tuyến.
Suy ra D là trung điểm AC.
Do đó AD = DC = (1).
Chứng minh tương tự, ta được AE = EB = (2).
Vì ∆ABC cân tại A nên AB = AC (3).
Từ (1), (2), (3), ta suy ra AD = AE.
Do đó ∆ADE cân tại A (định nghĩa tam giác cân)
Suy ra đáp án C đúng.
Đáp án A, B, D sai vì các tam giác đó không có hai cạnh nào trong mỗi tam giác bằng nhau.
Vậy ta chọn đáp án C.
Câu 4. Hoàn thành định nghĩa của tam giác cân:
Tam giác cân là tam giác:
A. Có hai đường cao bằng nhau;
B. Có hai đường trung tuyến bằng nhau;
C. Có hai cạnh bằng nhau;
D. Có hai tia phân giác trong bằng nhau.
Đáp án đúng là: C
Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
Vậy ta chọn đáp án C.
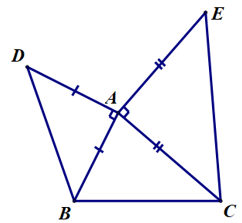
Câu 5. Cho ∆ABC có AB < AC. Ở phía ngoài ∆ABC, vẽ ∆ABD và ∆ACE vuông cân tại A. So sánh AD và AE.
A. AD < AE;
B. AD > AE;
C. AD = AE;
D. Không thể so sánh được.
Đáp án đúng là: A
Vì ∆ABD vuông cân tại A nên AB = AD (1).
Vì ∆ACE vuông cân tại A nên AC = AE (2).
Lại có AB < AC (giả thiết) (3).
Từ (1), (2), (3), ta suy ra AD < AE.
Vậy ta chọn đáp án A.
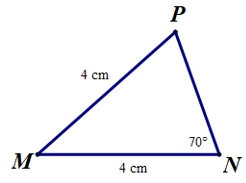
Câu 6. Tìm số đo ở hình bên:
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: B
Vì MN = MP (= 4 cm).
Nên ∆MNP cân tại M.
Suy ra (tính chất tam giác cân)
∆MNP có: (định lí tổng ba góc trong tam giác)
Suy ra .
Khi đó ta có .
Vậy .
Do đó ta chọn đáp án B.
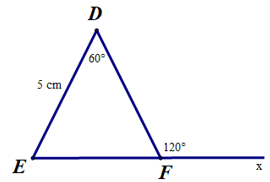
Câu 7. Cho hình bên dưới.
Độ dài cạnh EF bằng:
A. 2,5 cm;
B. 6 cm;
C. 5 cm;
D. 10 cm.
Đáp án đúng là: C
Ta có (hai góc kề bù).
Suy ra .
Do đó .
Suy ra ∆DEF cân tại D (dấu hiệu nhận biết)
Mà .
Suy ra ∆DEF là tam giác đều.
Suy ra EF = DF = DE = 5 cm.
Vậy ta chọn đáp án C.
Câu 8. Cho ∆PQR có , . ∆PQR là tam giác gì?
A. Tam giác đều;
B. Tam giác vuông;
C. Tam giác cân;
D. Tam giác vuông cân.
Đáp án đúng là: C
∆PQR có: (định lí tổng ba góc của tam giác)
Suy ra .
Do đó ta có .
Suy ra ∆PQR cân tại R (dấu hiệu nhận biết)
Do đó đáp án C đúng.
Vì cả ba góc của ∆PQR đều không bằng nhau và không bằng 60° nên ∆PQR không thể là tam giác đều.
Do đó đáp án A sai.
Vì ∆PQR không có góc nào bằng 90° nên ∆PQR không thể là tam giác vuông.
Do đó đáp án B, D sai.
Vậy ta chọn đáp án C.
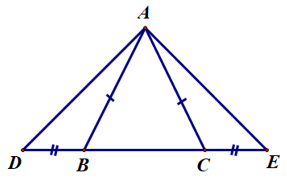
Câu 9. Cho ∆ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Hỏi ∆ADE là tam giác gì?
A. Tam giác cân;
B. Tam giác đều;
C. Tam giác vuông cân;
D. Tam giác vuông.
Đáp án đúng là: A
Vì ∆ABC cân tại A nên ta có (1).
Ta có (hai góc kề bù) (2).
Lại có (hai góc kề bù) (3).
Từ (1), (2), (3), ta suy ra .
Xét ∆ABD và ∆ACE, có:
AB = AC (∆ABC cân tại A),
(chứng minh trên),
BD = CE (giả thiết).
Do đó ∆ABD = ∆ACE (c.g.c).
Suy ra AD = AE (cặp cạnh tương ứng).
Do đó ∆ADE cân tại A (dấu hiệu nhận biết).
Vậy ta chọn đáp án A.
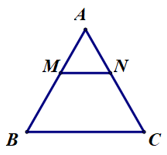
Câu 10. Cho ∆ABC đều. Lấy điểm M, N trên các cạnh AB, AC sao cho AM = AN. ∆AMN là tam giác gì?
A. Tam giác cân tại A;
B. Tam giác cân tại M;
C. Tam giác cân tại N;
D. Tam giác đều.
Đáp án đúng là: D
Vì AM = AN (giả thiết).
Nên ∆AMN là tam giác cân tại A.
Mà (do ∆ABC đều).
Suy ra ∆AMN là tam giác đều.
Vậy ta chọn đáp án D.
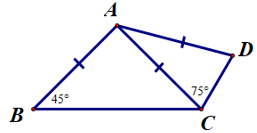
Câu 11. Cho hình vẽ bên.
Số đo bằng:
A. 45°;
B. 60°;
C. 90°;
D. 120°.
Đáp án đúng là: D
Ta có AB = AC nên ∆ABC cân tại A.
Do đó (tính chất tam giác cân)
∆ABC có: (định lí tổng ba góc trong tam giác)
Suy ra .
Ta có AC = AD nên ∆ACD cân tại A.
Do đó .
∆ACD có: (định lí tổng ba góc trong tam giác)
Suy ra .
Ta có .
Vậy ta chọn đáp án D.
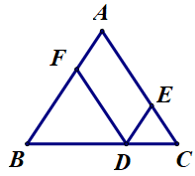
Câu 12. Cho ∆ABC cân tại A có cạnh bên bằng 3 cm. Gọi D là một điểm thuộc cạnh đáy BC. Qua D, kẻ các đường thẳng song song với các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E. Tổng DE + DF bằng:
A. 1,5 cm;
B. 3 cm;
C. 4,5 cm;
D. 6 cm.
Đáp án đúng là: B
Ta có DF // AC (giả thiết).
Do đó (hai góc đồng vị) .
Mà (do ∆ABC cân tại A).
Suy ra hay .
Do đó ∆BDF cân tại F (dấu hiệu nhận biết).
Suy ra BF = DF (1).
Ta có DF // AE và DE // AF (giả thiết).
Suy ra tứ giác AEDF là hình bình hành.
Suy ra DE = AF (2).
Từ (1), (2), ta suy ra DE + DF = AF + BF = AB = 3 cm.
Vậy ta chọn đáp án B.
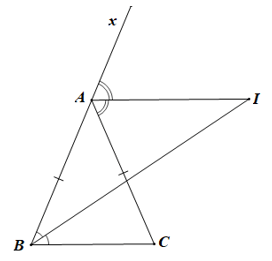
Câu 13. Cho ∆ABC cân tại A. Vẽ đường phân giác trong của và đường phân giác ngoài của , chúng cắt nhau tại I. Khẳng định nào sau đây đúng?
A. ∆ABI cân tại B;
B. AI // BC;
C. ∆ABI cân tại I;
D. ∆ABI vuông cân tại I.
Đáp án đúng là: B
Ta có ∆ABC cân tại A.
Suy ra .
∆ABC: (định lí tổng ba góc trong tam giác)
Suy ra .
Do đó (1).
Ta có: (hai góc kề bù).
Suy ra
Hay (do AI là phân giác của ).
Do đó (2).
Từ (1), (2), ta suy ra .
Mà hai góc này ở vị trí so le trong.
Ta suy ra AI // BC.
Do đó đáp án B đúng.
Vì AI // BC nên (hai góc so le trong).
Mà (do BI là phân giác của ).
Do đó .
Suy ra ∆ABI cân tại A (dấu hiệu nhận biết).
Do đó đáp án A, C, D sai.
Vậy ta chọn đáp án B.
Câu 14. Cho ∆ABC cân tại A, tia phân giác trong của cắt BC tại D. Khẳng định nào dưới đây sai?
A. D là trung điểm BC;
B. ;
C. ∆ADB = ∆ADC;
D. .
Đáp án đúng là: D
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung,
(do AD là tia phân giác của ),
AB = AC (do ∆ABC cân tại A).
Do đó ∆ADB = ∆ADC (c.c.c).
Suy ra đáp án C đúng.
Ta có ∆ADB = ∆ADC (chứng minh trên).
Suy ra BD = CD và (cặp cạnh và cặp góc tương ứng).
Vì BD = CD nên D là trung điểm BC.
Do đó đáp án A đúng.
Ta có (hai góc kề bù).
Suy ra .
Do đó AD ⊥ BC.
∆ABD vuông tại D: .
Mà (AD là phân giác của ).
Suy ra .
Do đó đáp án B đúng.
Ta có .
Suy ra .
Do đó .
Do đó đáp án D sai.
Vậy ta chọn đáp án D.
Câu 15. Cho ∆ABC vuông tại A có . Kẻ AH ⊥ BC tại H và tia phân giác AD của (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?
A. ∆ADH = ∆ADE;
B. DE ⊥ AC;
C. ∆ACF đều;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Ta xét từng đáp án:
Đáp án A:
Xét ∆ADH và ∆ADE, có:
AH = AE (giả thiết).
(do AD là phân giác của ).
AD là cạnh chung.
Do đó ∆ADH = ∆ADE (c.g.c)
Suy ra đáp án A đúng.
Đáp án B:
∆ADH = ∆ADE (chứng minh trên).
Suy ra (cặp góc tương ứng).
Mà (do AH ⊥ HD).
Do đó .
Khi đó ta có DE ⊥ AE hay DE ⊥ AC.
Do đó đáp án B đúng.
Đáp án C:
Ta có AH = AE (giả thiết) và HF = EC (giả thiết).
Suy ra AH + HF = AE + EC.
Do đó AF = AC.
Khi đó ta có ∆ACF cân tại A (1).
Vì ∆AHC vuông tại H nên .
Do đó (2).
Từ (1), (2), ta suy ra ∆ACF là tam giác đều.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác:
Trắc nghiệm Toán 7 Bài 8: Đường vuông góc và đường xiên
Trắc nghiệm Toán 7 Bài 9: Đường trung trực của một đoạn thẳng
Trắc nghiệm Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác
Trắc nghiệm Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác
Trắc nghiệm Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác
Xem thêm các chương trình khác: