TOP 15 câu Trắc nghiệm Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác (Cánh diều 2024) có đáp án - Toán 7
Bộ 15 câu hỏi trắc nghiệm Toán lớp 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác có đáp án đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 2.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 7 Cánh diều bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 033000255833 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác - Cánh diều
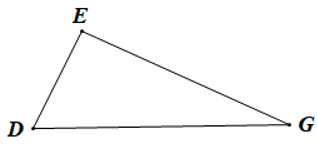
Câu 1. Cho tam giác DEG có DE + EG = 15 cm, DE – EG = 7 cm . Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: B
Vì DE – EG = 7 cm (giả thiết) nên DE = EG + 7 (cm)
Ta có DE + EG = 15 cm (giả thiết)
Hay EG + 7 + EG = 15
Suy ra 2. EG = 15 – 7 = 8
Do đó EG = 4 (cm)
Khi đó DE = 4 + 7 = 11 (cm)
Xét tam giác DEG có DE > EG (11 cm > 4 cm)
Mà cạnh DE đối diện với góc G, cạnh EG đối diện với góc D.
Nên (quan hệ giữa góc và cạnh đối diện trong tam giác)
Vậy ta chọn đáp án B.
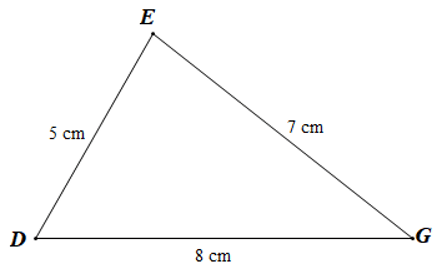
Câu 2. Cho tam giác DEG có DE = 5 cm, EG = 7 cm, DG = 8 cm . Khẳng định nào sau đây là đúng?
A. Góc D là góc nhỏ nhất trong tam giác DEG;
B. Góc E là góc nhỏ nhất trong tam giác DEG;
C. Góc G là góc nhỏ nhất trong tam giác DEG;
D. Góc D là góc lớn nhất trong tam giác DEG.
Đáp án đúng là: C
Vì tam giác DEG có DG > EG > DE (8 cm > 7 cm > 5 cm) nên theo quan hệ giữa cạnh và góc trong tam giác ta có
Vậy góc G là góc nhỏ nhất trong tam giác DEG.
Câu 3. Cho tam giác MNP có MN > MP > NP. Trong các khẳng định sau, câu nào đúng?
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: C
Vì tam giác MNP có MN > MP > NP nên theo quan hệ giữa cạnh và góc trong tam giác ta có
Vậy ta chọn đáp án C.
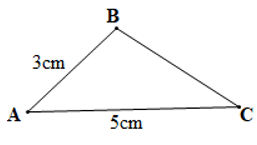
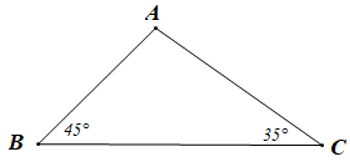
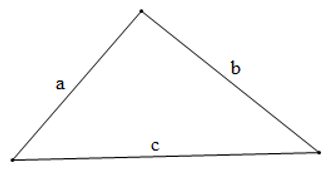
Câu 4. Cho hình vẽ dưới đây:
Khẳng định nào là đúng?
A.
B.
C.
D. Không so sánh được.
Đáp án đúng là: C
Xét tam giác ABC có AC > AB (5 cm > 3 cm)
Mà góc B đối diện với cạnh AC, góc C đối diện với cạnh AB.
Nên (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn)
Vậy ta chọn đáp án C.
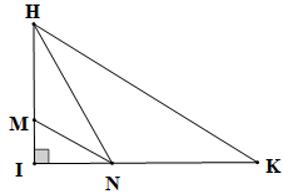
Câu 5. Cho ∆HIK vuông tại I. Trên cạnh IH lấy điểm M, trên cạnh IK lấy điểm N. So sánh độ dài các cạnh MN, HN, HK.
A. HN < MN < HK;
B. MN = HN < HK;
C. MN < HN < HK;
D. MN > HN = HK.
Đáp án đúng là: C
Xét DMIN vuông tại I có là góc ngoài của tam giác tại đỉnh M
Nên (tính chất góc ngoài của tam giác)
Mà do đó
Khi đó góc HMN là góc tù.
Mà trong ∆HMN, cạnh HN đối diện với góc tù HMN.
Nên HN là cạnh lớn nhất (cạnh đối diện với góc lớn hơn)
Suy ra MN < HN (1)
Tương tự ta cũng có là góc ngoài tại đỉnh N của tam giác vuông HIN nên là góc tù.
Do đó, trong tam giác HNK, cạnh HK đối diện với góc tù là cạnh lớn nhất
Suy ra HN < HK (2)
Từ (1) và (2) ta có: MN < HN< HK.
Vậy ta chọn phương án C.
Câu 6. Xét các khẳng định:
(1) Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất;
(2) Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất;
(3) Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhọn;
(4) Trong một tam giác, đối diện với cạnh lớn nhất là góc tù.
Chọn câu đúng nhất:
A. Chỉ có (1) đúng;
B. Cả (1) và (2) đều đúng;
C. Cả (1), (2) và (3) đều đúng;
D. Cả (1), (2), (3)và (4) đều đúng.
Đáp án đúng là: C
+) Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh đối diện với góc vuông là cạnh lớn nhất (quan hệ giữa cạnh và góc trong tam giác) nên đẳng định (1) đúng.
+) Trong tam giác tù, góc tù là góc lớn nhất nên cạnh đối diện với góc tù là cạnh lớn nhất (quan hệ giữa cạnh và góc trong tam giác) nên khẳng định (2) đúng.
+) Trong một tam giác, góc nhỏ nhất là góc nhọn, nên đối diện với cạnh nhỏ nhất là góc nhọn (quan hệ giữa cạnh và góc trong tam giác) nên khẳng định (3) đúng.
+) Trong tam giác tù góc lớn nhất là góc tù, trong tam giác vuông góc lớn nhất là góc vuông, trong tam giác nhọn có một góc nhọn lớn nhất nên trong một tam giác bất kì, đối diện với cạnh lớn nhất chưa chắc đã là góc tù mà có thể là góc nhọn hoặc góc vuôngnên khẳng định (4) sai.
Vậy ta chọn đáp án C.
Câu 7. Ba cạnh của một tam giác có độ dài lần lượt là 6 cm, 7 cm, 8cm. Chọn khẳng định đúng:
A. Góc lớn nhất là góc đối diện với cạnh có độ dài 6 cm;
B. Góc lớn nhất là góc đối diện với cạnh có độ dài 7 cm;
C. Góc lớn nhất là góc đối diện với cạnh có độ dài 8 cm;
D. Góc nhỏ nhất là góc đối diện với có độ dài 7 cm.
Đáp án đúng là: C
Vì trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn, mà cạnh 8 cm là cạnh lớn nhất nên góc đối diện với cạnh có độ dài 8 cm là góc lớn nhất.
Vậy ta chọn đáp án C.
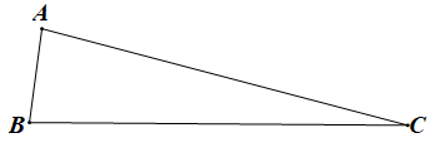
Câu 8. Cho tam giác ABC có Khẳng định nào sau đây là đúng?
A. AB < AC < BC;
B. AB > AC > BC;
C. AB > BC > AC;
D. AB < BC < AC.
Đáp án đúng là: A
Xét tam giác ABC có: ( định lí tổng ba góc trong một tam giác)
Suy ra
Mà
Do đó hay
Vì tam giác ABC có nên theo quan hệ giữa cạnh và góc trong tam giác ta có BC > AC > AB
Vậy ta chọn đáp án A.
Câu 9. Cho tam giác ABC có AB = 1 cm, AC = 4 cm. Độ dài cạnh BC có thể là:
A.BC = 2 cm;
B. BC = 3 cm;
C. BC = 4 cm;
D.BC = 5 cm.
Đáp án đúng là: C
Áp dụng bất đẳng thức cho tam giác ABC ta có:
AC – AB < BC < AC + AB
Hay 4 – 1 < BC < 4 + 1
Suy ra 3 < BC < 5.
Trong các phương án thì chỉ có phương án C (BC = 4 cm) thỏa mãn điều kiện trên.
Vậy độ dài cạnh BC có thể là 4 cm.
Ta chọn phương án C.
Câu 10. Dựa vào bất đẳng thứ tam giác, kiểm tra xem bộ ba độ dài cho sau đây không thể là độ dài ba cạnh của một tam giác?
A. 2 cm, 5 cm, 7 cm;
B. 3 cm, 5 cm, 7 cm;
C. 4 cm, 5 cm, 6 cm;
D. 3 cm, 5 cm, 6 cm.
Đáp án đúng là: A
+) Xét bộ ba độ dài: 2 cm, 5 cm, 7 cm
Ta có: 2 + 5 = 7 không thỏa mãn bất đẳng thức tam giác.
Do đó bộ ba độ dài 2 cm, 5 cm, 7 cm không thể là độ dài ba cạnh của một tam giác.
+) Xét bộ ba: 3 cm, 5 cm, 7 cm
Ta có: 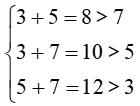
Do đó bộ ba độ dài 3 cm, 5 cm, 7 cm là độ dài ba cạnh của một tam giác.
+) Xét bộ ba: 4 cm, 5 cm, 6 cm
Ta có: 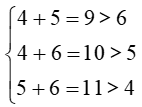
Do đó bộ ba độ dài 4 cm, 5 cm, 6 cm là độ dài ba cạnh của một tam giác.
+) Xét bộ ba: 3 cm, 5 cm, 6 cm
Ta có: 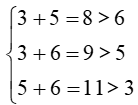
Do đó bộ ba độ dài 3 cm, 5 cm, 6 cm là độ dài ba cạnh của một tam giác.
Vậy ta chọn đáp án A.
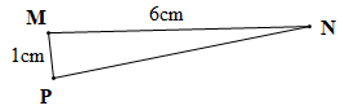
Câu 11. Cho tam giác MNP có MN = 6 cm, MP = 1 cm. Độ dài cạnh NP là một số tự nhiên lớn hơn 0 (cm). Tam giác MNP có:
A.MN = NP;
B. NP > MP;
C.Cả A và B đều sai;
D. Cả A và B đều đúng.
Đáp án đúng là: D
Áp dụng bất đẳng thức cho tam giác MNP ta có:
MN – MP < NP < MN + MP
Hay 6 – 1 < NP < 6 + 1
Suy ra 5 < NP < 7
Mà độ dài của NP là số tự nhiên lớn hơn 0
Nên NP = 6 cm
Hay NP = MN (= 6 cm). Do đó A đúng.
Mà MP = 1 cm nên NP > MN.
Do đó B đúng.
Vậy ta chọn phương án D.
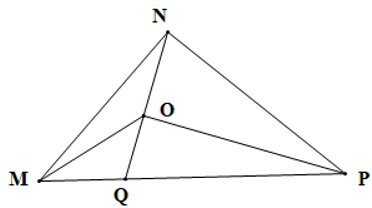
Câu 12. Cho hình vẽ sau:
Khẳng định nào sau đây là đúng?
A. ON + OP > MN + MP;
B. ON + OP = MN + MP;
C. ON + OP < MN + MP;
D. ON + OP ≥ MN + MP.
Đáp án đúng là: C
Xét ∆OPQ có OP < OQ + PQ (bất đẳng thức trong tam giác)
Xét ∆QNM có QN < MQ + MN (bất đẳng thức trong tam giác)
Suy ra OP + QN < OQ + PQ + MQ + MN
Hay OP + ON + OQ < OQ + MP + MN
Nên OP + ON < MP + MN
Vậy ta chọn đáp án C.
Câu 13. Chọn câu sai. Trong một tam giác:
A. Độ dài một cạnh luôn lớn hơn nửa chu vi;
B. Độ dài một cạnh luôn nhỏ hơn nửa chu vi;
C. Độ dài một cạnh luôn nhỏ hơn chu vi;
D. Độ dài một cạnh luôn nhỏ hơn tổng hai cạnh còn lại.
Đáp án đúng là: A
Xét một tam giác có độ dài ba cạnh là a, b, c (a, b, c > 0)
Theo bất đẳng thức trong tam giác ta có a < b + c.
Nên a + a < b + c + a
Suy ra 2.a < b + c + a
Hay a <
Chứng minh tương tự ta cũng có:
và
Vậy ta chọn phương án A.
Câu 14. Có bao nhiêu tam giác có độ dài hai cạnh là 3 cm, 9 cm và độ dài cạnh còn lại là một số nguyên (cm)?
A. 4;
B. 5;
C. 6;
D. 7.
Đáp án đúng là: B
Gọi độ dài cạnh còn lại của tam giác là x (x > 0).
Theo bất đẳng thức tam giác ta có:
9 – 3 < x < 9 + 3
Do đó 6 < x < 12.
Mà x là số nguyên nên ta có x ∈ {7; 8; 9; 10; 11}.
Vậy có 5 giá trị x nên có 5 tam giác thỏa mãn yêu cầu đề bài.
Ta chọn phương án B.
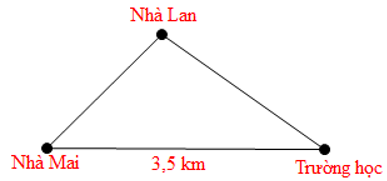
Câu 15. Ba vị trí của nhà Mai, nhà Lan và trường học được mô tả như hình vẽ dưới đây.
Trong buổi sáng hôm nay, Mai phải đến nhà Lan để lấy đồ trước khi đến trường.
Bạn Mai nói rằng tổng quãng đường mà Mai đã đi khoảng 3 km.
Bạn Lan nói rằng tổng quãng đường mà Mai đã đi khoảng 4 km.
Bạn Minh nói rằng tổng quãng đường mà Mai đã đi khoảng 5 km.
Chọn khẳng định đúng:
A. Chỉ bạn Mai nói sai;
B. Chỉ bạn Lan nói sai;
C. Bạn Lan và Minh nói sai.
D. Cả ba bạn nói sai.
Đáp án đúng là: A
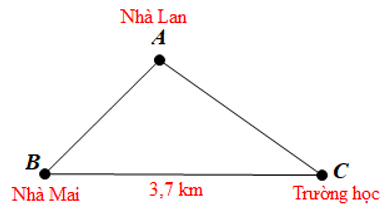
Đặt ba điểm tại ba vị trí như hình vẽ trên.
Theo bất đẳng thức ta có:
AB + AC > BC
Nên AB + AC > 3,7 cm.
Do đó tổng quãng đường từ nhà Mai đến nhà Lan rồi từ nhà Lan tới trường học phải lớn hơn 3,7 km.
Vậy nên bạn Mai đã nói sai.
Ta chọn phương án A.
Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác:
Trắc nghiệm Toán 7 Bài 3: Hai tam giác bằng nhau
Trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
Trắc nghiệm Toán 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
Trắc nghiệm Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
Xem thêm các chương trình khác: