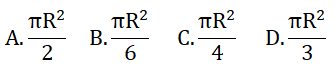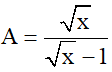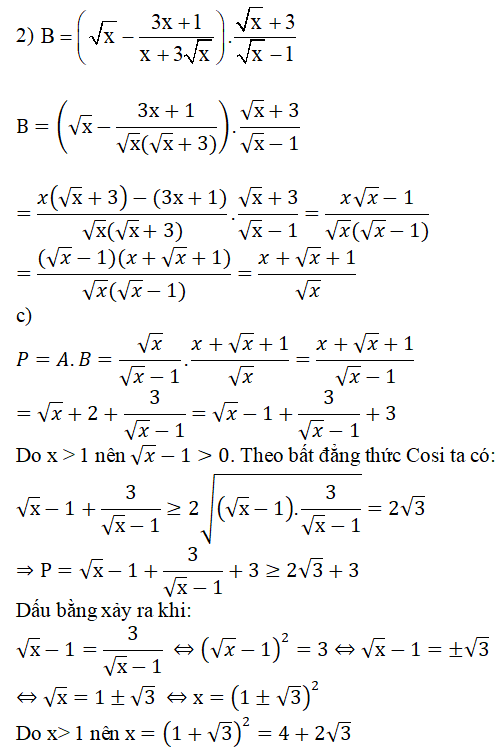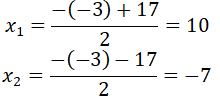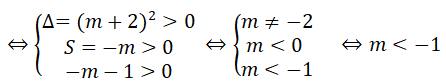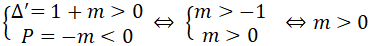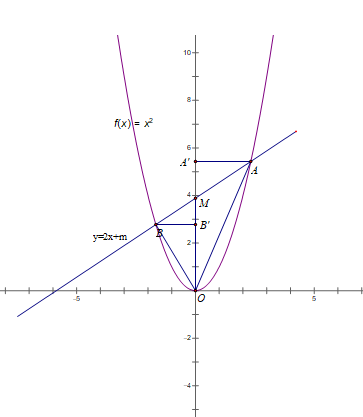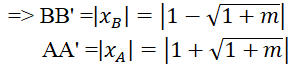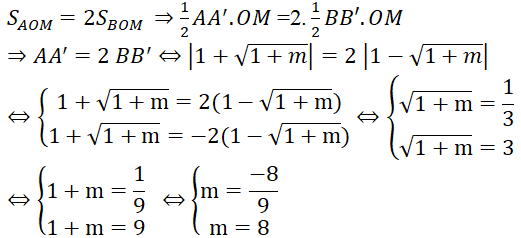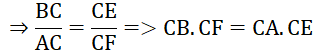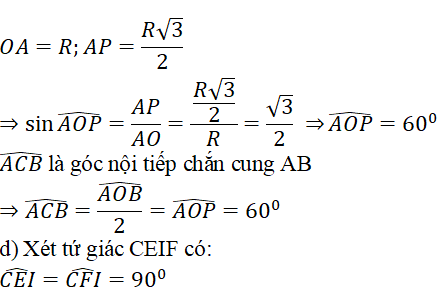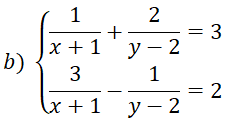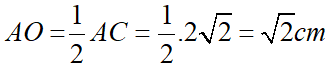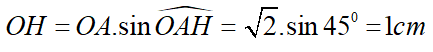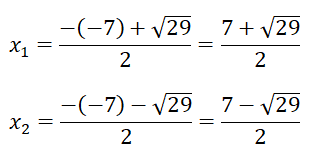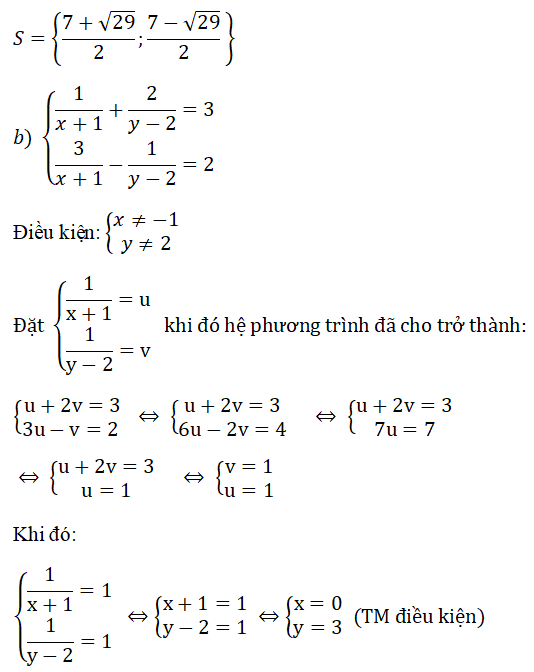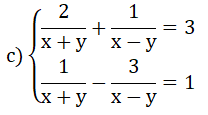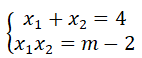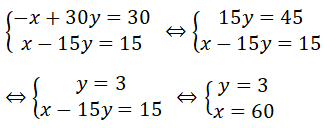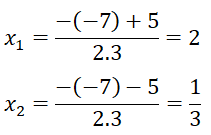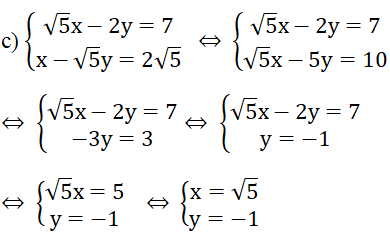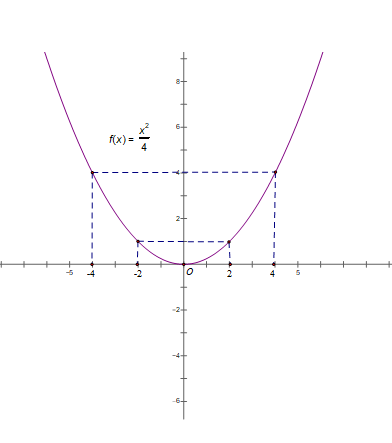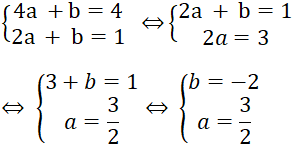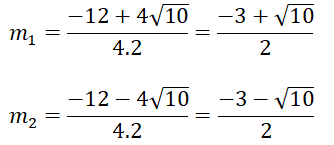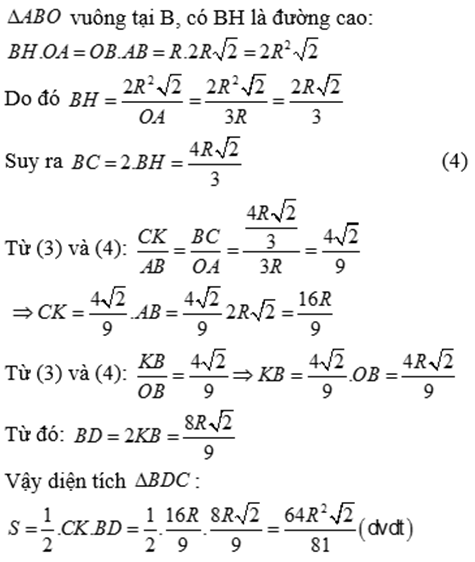TOP 15 Đề thi Học kì 2 Toán 9 năm 2024 có đáp án
Bộ 15 Đề thi Học kì 2 Toán lớp 9 năm 2023 - 2024 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 9 học kì 2. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi Toán 9 bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi Học kì 2 Toán lớp 9 năm 2023 - 2024 có đáp án
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 1
Phần I. Trắc nghiệm (2 điểm)
Câu 1: Phương trình 4x – 3y =-1 nhận cặp số nào sau đây là một nghiệm?
A. (-1;-1)
B. (-1;1)
C. (1;-1)
D. (1;1)
Câu 2: Phương trình nào dưới đây có thể kết hợp với phương trình x + y = 1 để được một hệ phương trình có nghiệm duy nhất?
A. x + y = -1
B. 0.x + y = 1
C. 2y = 2 - 2x
D. 3y = -3x + 3
Câu 3: Cho hàm số y=23x2. Kết luận nào sau đây là đúng?
A. Hàm số trên luôn đồng biến
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0 và nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0 và nghịch biến khi x > 0
Câu 4: Điểm P(-1;-2) thuộc đồ thị hàm số y = m.x2 khi m bằng:
A. 2
B. -2
C. 4
D. -4
Câu 5: Tổng hai nghiệm của phương trình 2x2+5x-3=0 là:
A. 52
B. −52
C. −32
D. 32
Câu 6; Cho đường tròn(O ; R ) dây cung AB=R√2. Khi đó góc AOB có số đo bằng?
A. 200
B. 300
C. 600
D. 900
Câu 7. Cho các số đo như hình vẽ, biết MON . Độ dài cung là:
![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/hinh-1649132269.png)
A.
B.
C.
D.
Câu 8: Cho ABC vuông tại A, AC = 3cm, AB = 4cm. Quay tam giác đó một vòng quanh cạnh AB được một hình nón. Diện tích xung quanh của hình nón đó là:
A. 10p(cm2)
B. 15p(cm2)
C. 20p(cm2)
D. 24p(cm2)
Phần II. Tự luận (8đ)
Bài 1:
a) Giải hệ phương trình:
b) Giải phương trình : (x + 3)2 = (x2 – 2x)2
Bài 2: Cho phương trình ẩn x, tham số m: x2 – mx + m – 1 = 0
a) Chứng tỏ phương trình đã cho luôn có nghiệm với mọi m
b) Gọi x1 và x2 là hai nghiệm của phương trình đã cho. Tìm giá trị của m để x12.x2 + x1.x22 = 2.
Bài 3: Cho (O; R) và một điểm A ở ngoài đường tròn. Qua A kẻ các tiếp tuyến AB và AC với đường tròn ( B và C là các tiếp điểm). Gọi H giao điểm của AO và BC. Chứng minh:
a) ABOC là tứ giác nội tiếp
b) Kẻ đường kính BD của (O) ,vẽ CK vuông góc với BD .
Chứng minh :AC.CD = AO.CK
c) AD cắt CK ở I .Chứng minh I là trung điểm của CK
Bài 4 : Cho 361 số tự nhiên thỏa mãn điều kiện :
Chứng minh rằng trong 361 số tự nhiên đó ,tồn tại ít nhất 2 số bằng nhau
HƯỚNG DẪN GIẢI
Phần I. Trắc nghiệm (2 điểm)
Câu 1: Phương trình 4x – 3y =1 nhận cặp số nào sau đây là một nghiệm?
A. (-1;-1)
B. (-1;1)
C. (1;-1)
D. (1;1)
Hướng dẫn giải
Đáp án đúng là A
+) Thay x = -1 và y = -1 vào phương trình đã cho ta được: 4.(-1) – 3.(-1) = -1⇔ -1 = -1 (luôn đúng). Do đó cặp số (-1; -1) là nghiệm của phương trình đã cho.
+) Thay x = -1 và y = 1 vào phương trình đã cho ta được: 4.(-1) – 3.1 = -1 ⇔ -7 = -1 (vô lý). Do đó cặp số (-1; 1) không là nghiệm của phương trình đã cho.
+) Thay x = 1 và y = -1 vào phương trình đã cho ta được: 4.1 – 3.(-1) = 7 ⇔ 7 = -1 (vô lý). Do đó cặp số (1; -1) không là nghiệm của phương trình đã cho.
+) Thay x = 1 và y = 1 vào phương trình đã cho ta được: 4.1 – 3.1 = -1 ⇔ 1 = -1 (vô lý). Do đó cặp số (1; 1) không là nghiệm của phương trình đã cho.
Câu 2: Phương trình nào dưới đây có thể kết hợp với phương trình x + y = 1 để được một hệ phương trình có nghiệm duy nhất?
A. x + y = 1
B. 0.x + y = 1
C. 2y = 2 - 2x
D. 3y = -3x + 3
Hướng dẫn giải
Đáp án đúng là B
Tập nghiệm của phương trình x + y = 1 được biểu diễn bởi đường thẳng d1: y = -x + 1
Tập nghiệm của phương trình x + y = -1 được biểu diễn bởi đường thẳng d2: y = -x – 1
Tập nghiệm của phương trình 0.x + y = 1 được biểu diễn bởi đường thẳng d3: y = 1
Tập nghiệm của phương trình 2y = 2 - 2x được biểu diễn bởi đường thẳng d4: y = - x + 1
Tập nghiệm của phương trình 3y = -3x + 3 được biểu diễn bởi đường thẳng d5: y = - x + 1
Ta có:
+) d1//d2 do đó hai phương trình không có nghiệm chung.
+) d3 cắt d2 tại điểm có tọa độ (2; 1) nên hai phương trình này có một nghiệm chung.
+) d4 trùng d1 nên hai phương trình có vô số nghiệm chung.
+) d5 trùng d1 nên hai phương trình có vô số nghiệm chung.
Vậy phương trình 0.x + y = 1 và phương trình đã cho tạo với nhau một hệ có một nghiệm duy nhất
Câu 3: Cho hàm số . Kết luận nào sau đây là đúng?
A. Hàm số trên luôn đồng biến
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0 và nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0 và nghịch biến khi x > 0
Hướng dẫn giải
Đáp án đúng là C
Hàm số có khi đó hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
Câu 4: Điểm P(-1;-2) thuộc đồ thị hàm số y = m.x2 khi m bằng:
A. 2
B. -2
C. 4
D. -4
Hướng dẫn giải
Đáp án đúng là B
Vì điểm P thuộc đồ thị hàm số nên thay x = - 1 và y = -2 vào hàm số ta được: -2 = m.(-1)2 ⇔ m = -2.
Vậy với m = -2 thì điểm P thuộc đồ thị hàm số đã cho.
Câu 5: Tổng hai nghiệm của phương trình 2x2+5x-3=0 là:
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là B
Xét phương trình bậc hai 2x2 + 5x – 3 = 0 có a = 2, b = 5, c = -3 và
∆ = b2 – 4ac = 52 – 4.2.(-3) = 25 + 24 = 49 > 0
Do đó phương trình có hai nghiệm phân biệt:
Suy ra
Câu 6; Cho đường tròn(O ; R ) dây cung . Khi đó góc AOB có số đo bằng?
A. 200
B. 300
C. 600
D. 900
Hướng dẫn giải
Đáp án đúng là D
![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/bai-gia-1649133301.png)
Kẻ đường thẳng OH vuông góc với AB tại H
Suy ra H là trung điểm của AB
Xét ∆OHA vuông tại H, có:
Xét ∆AOB có OA = OB = R nên tam giác AOB cân tại O
Mà OH là đường cao nên OH là phân giác
Câu 7. Cho các số đo như hình vẽ, biết . Độ dài cung là:
![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/hinh-1649132269.png)
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là B
Độ dài cung là
Câu 8: Cho ABC vuông tại A, AC = 3cm, AB = 4cm. Quay tam giác đó một vòng quanh cạnh AB được một hình nón. Diện tích xung quanh của hình nón đó là:
A. 10p(cm2)
B. 15p(cm2)
C. 20p(cm2)
D. 24p(cm2)
Hướng dẫn giải
Đáp án đúng là B
![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/8-1649133545.png)
Xét ∆ABC vuông tại A, có:
BC2 = AB2 + AC2 (định lý Py – ta – go)
BC2 = 32 + 42
BC2 = 25
BC = 5 (cm)
Đường sinh của hình nón chính là BC nên l = 5 (cm)
Bán kính đáy là cạnh AC, ta có: R = 3 (cm).
Khi đó diện tích xung quanh của hình nón là: (cm2)
Vậy diện tích xung quanh của hình nón sinh bởi tam giác ABC là cm2.
Phần II. Tự luận (8đ)
Bài 1:
a) Giải hệ phương trình:
Vậy nghiệm của hệ phương trình là (1; 4).
b) Giải phương trình : (x + 3)2 = (x2 – 2x)2
Xét phương trình: (x + 3)2 = (x2 – 2x)2
⇔ (x + 3)2 – (x2 – 2x)2 = 0
⇔ (x + 3 – x2 + 2x)(x + 3 + x2 – 2x) = 0
⇔ (– x2 + 3x + 3)(x2 – x + 3) = 0
TH1: – x2 + 3x + 3 = 0 (1)
Ta có: ∆ = 32 – 4.(-1).3 = 9 + 12 = 21 > 0
Suy ra phương trình (1) có hai nghiệm phân biệt
TH2: x2 – x + 3 (2)
Ta có: ∆ = (-1)2 – 4.1.3 = 1 – 12 = -11 < 0
Suy ra phương trình (2) vô nghiệm.
Vậy phương trình đã cho có 2 nghiệm
Bài 2:
a) Xét phương trình: x2 – mx + m – 1 = 0, có:
∆ = (-m)2 – 4.(m – 1) = m2 – 4m + 4 = (m – 2)2 ≥ 0 với mọi m
Vậy phương trình đã cho luôn có nghiệm với mọi m.
b. Gọi x1 và x2 là hai nghiệm của phương trình đã cho.
Áp dụng định lý Vi – ét, ta có:
Xét biểu thức x12.x2 + x1.x22 = 2.
Vậy với m = 0 ; m = 1 thì phương trình đã cho có hai nghiệm thỏa mãn điều kiện của bài toán.
Bài 3:
Vẽ hình đúng
![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/gg-1649134046.png) a) ABOC là tứ giác nội tiếp vì có tổng hai góc đối
a) ABOC là tứ giác nội tiếp vì có tổng hai góc đối
b) (g.g)
c) Ta có : CK // AB ( cùng vuông góc với BD ) nên: IK // AB
Xét ∆ABD có IK // AB (cmt)
Do đó: ( định lí ta lét )
=> IK.DB = AB.KD (1)
Lại có (cmt)
Mà: AC = AB ( tính chất 2 tiếp tuyến cắt nhau ); CO = OB = R (2)
Từ (1) và (2) ta có : IK.DB = CK.OB hay IK . 2R = CK . R
Do đó CK = 2IK.
Suy ra I là trung điểm của CK.
Bài 4:
Giả sử trong 361 số tự nhiên đó không tồn tại hai số nào bằng nhau
Không mất tính tổng quát, giả sử
Do nên:
Mà
Hay (Trái với giả thiết)
Vậy Trong 361 số tự nhiên đó , tồn tại ít nhất hai số bằng nhau.
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 2
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Bài 1 (2,5 điểm):
1. Giải hệ phương trình:
2.
a) Vẽ đồ thị hàm số y = 2x + 2.
b) Xác định hàm số y = ax + b có đồ thị là đường thẳng (d), biết đường thẳng (d) đi qua điểm M(-1 ; 2) và song song với đường thẳng y = 2x + 2.
Bài 2 (2,0 điểm): Cho phương trình ẩn x: (1)
a) Giải phương trình (1) với m = -2
b) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt với mọi m.
c) Gọi hai nghiệm của phương trình (1) là x1, x2 Tìm giá trị của m để x1, x2 là độ dài hai cạnh của một tam giác vuông có cạnh huyền bằng
Bài 3 (2,0 điểm): Giải bài toán sau bằng cách lập phương trình :
Một xe khách và một xe du lịch khởi hành đồng thời từ A đến B. Biết vận tốc của xe du lịch lớn hơn vận tốc xe khách là 20km/h. Do đó đến B trước xe khách là 50 phút. Tính vận tốc của mỗi xe, biết quãng đường AB dài 100km.
Bài 4 (3,5 điểm):
Cho hình vuông ABCD, điểm M thuộc cạnh BC (M khác B, C). Qua B kẻ đường thẳng vuông góc với DM, đường thẳng này cắt các đường thẳng DM và DC theo thứ tự tại H và K.
a. Chứng minh: Các tứ giác ABHD, BHCD nội tiếp đường trò
b. Tính
c. Chứng minh KH.KB = KC.KD
d. Đường thẳng AM cắt đường thẳng DC tại N. Chứng minh
HƯỚNG DẪN GIẢI
Bài 1:
1. Ta có:
Vậy hệ phương trình có nghiệm (x,y) = (-3 ; -5).
2.
a) Cho x = 0 Þ y = 2, ta được A(0 ; 2) Î Oy
Cho y = 0 Þ x = -1, ta được B(-1 ; 0) Î Ox
Đồ thị hàm số y = 2x + 2 là đường thẳng đi qua hai điểm A và B
Vẽ đúng đồ thị hàm số y = 2x + 2:![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/do-1649137087.png)
b) Vì đường thẳng (d) song song với đường thẳng y = 2x + 2 nên
Ta có đường thẳng (d) đi qua điểm M(-1 ; 2)
Thay x = -1 và y = 2 vào đồ thị hàm số (d), ta có: -a + b = 2
Mà a = 2 nên b = 4 (thỏa mãn điều kiện)
Vậy hàm số cần tìm có dạng y = 2x + 4.
Bài 2:
a) Với m = -2 ta được phương trình x2 + 2x – 4 = 0
Ta có ∆’ = 12 – (-4) = 5 > 0
Do đó phương trình có hai nghiệm phân biệt:
Vậy với m = -2 tập nghiệm của phương trình đã cho là
b) Xét phương trình (1) có D’ = (m + 1)2 – 2m = m2 + 2m + 1 – 2m = m2 + 1
Vì m2 ≥ 0 với mọi m
Nên m2 + 1 > 0 với mọi m hay ∆’ > 0 với mọi m.
Vậy với mọi m thì phương trình có hai nghiệm phân biệt.
c) Theo b) phương trình (1) có hai nghiệm phân biệt x1, x2 với mọi m.
Áp dụng định lí Viét ta có:
Vì x1 và x2 là độ dài hai cạnh của một tam giác vuông có cạnh huyền bằng nên theo định lý Py – ta – go ta có:
Vậy với m = 1 hoặc m = -2 thì x1; x2 là độ dài hai cạnh của một tam giác vuông có cạnh huyền bằng
Bài 3.
Gọi vận tốc xe khách là x(km/h) (x > 0)
Vận tốc xe du lịch là x + 20 (km/h)
Thời gian xe khách đi từ A đến B là (h)
Thời gian xe du lịch đi từ A đến B là (h)
Do xe du lịch đến B trước xe khách 50 phút = giờ nên ta có phương trình:
⇔ 120x + 2 400 – 120x = x2 + 20x
⇔ x2 + 20x – 2 400 = 0
Trong hai giá trị ta thấy x = 40 thỏa mãn điều kiện. Do đó vận tốc của xe khách là 40km/h và vận tốc của xe du lịch là 40 + 20 = 60 km/h.
Vậy vận tốc của xe khách là 40km/h và vận tốc của xe du lịch là 40 + 20 = 60 km/h.
Bài 4.
Vẽ hình đúng:![[Năm 2022] Đề thi Học kì 2 Toán lớp 9 có đáp án (6 đề) (ảnh 1)](https://vietjack.me/storage/uploads/images/268/b4-1649142750.png)
a) Ta có: = 90o (ABCD là hình vuông) và = 90o (gt)
Mà hai góc ở vị trí đối nhau nên tứ giác ABHD nội tiếp đường tròn.
Ta có: = 90o (gt) và = 90o (ABCD là hình vuông)
Do đó H và C là hai đỉnh liên tiếp cùng nhìn cạnh DB dưới một góc bằng nhau nên tứ giác BHCD nội tiếp đường tròn.
b)
Theo ý a, tứ giác AHCD là nội tiếp đường tròn nên
Mà
Vì ABCD là hình vuông nên (tính chất hình vuông)
c) Xét DKHD và DKCB, có:
chung
⇒ DKHD ∽ DKCB (g.g)
=> => KH.KB = KC.KD (đpcm).
d) Qua A kẻ đường thẳng vuông góc với AM, đường thẳng này cắt đường thẳng DC tại P.
Xét ∆BAM và ∆DAP có:
(cùng phụ )
AB = AD (tính chất hình vuông ABCD)
⇒ BAM = DAP (g.c.g)
⇒ AM = AP (hai cạnh tương ứng)
Xét PAN vuông tại A, có: AD PN
(hệ thức lượng trong tam giác vuông)
Mà AP = AM (cmt)
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 3
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Bài 1 (1,5 điểm): Giải hệ phương trình
Bài 2 (2,0 điểm): Giải bài toán bằng cách lập phương trình và hệ phương trình:
Một mảnh đất hình chữ nhật có diện tích 720m2, nếu tăng chiều dài 6m và giảm chiều rộng 4m thì diện tích của mảnh vườn không đổi. Tính các kích thước của mảnh vườn đó.
Bài 3 (2,0 điểm):
Cho phương trình bậc hai ẩn x, ( m là tham số): (1)
a. Giải phương trình với m = 3.
b. Tìm điều kiện của m để phương trình (1) luôn có 2 nghiệm phân biệt.
Bài 4 (4,0 điểm):
1. Một lọ hoa hình trụ có đường kính đáy là 12cm, người ta đổ vào trong lọ một lượng nước với chiều cao cột nước là 20cm. Tính thể tích nước trong lọ hoa.
2. Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tai E. Kẻ EFAD. Gọi M là trung điểm của AE. Chứng minh rằng:
a. Tứ giác ABEF nội tiếp một đường tròn.
b. Tia BD là tia phân giác của góc CBF.
c. Tứ giác BMFC nội tiếp một đường tròn.
Bài 5 (0,5 điểm):
Cho ba số dương a, b, c thỏa mãn:
Tính giá trị nhỏ nhất của biểu thức
HƯỚNG DẪN GIẢI
Bài 1:
Xét hệ phương trình Điều kiện
Đặt Khi đó hệ phương trình đã cho tương đương với
(thỏa mãn điều kiện)
Vậy hệ phương trình đã cho có nghiệm là
Bài 2:
Gọi chiều dài của mảnh đất đó là x(m), x > 0
Chiều rộng của mảnh đất đó là (m)
Nếu tăng chiều dài 6m: x + 6 (m)
Và giảm chiều rộng 4m ta được: (m)
Thì diện tích mảnh vườn là:
Do diện tích mảnh vườn không đổi nên ta có phương trình:
⇔ 4x2 + 24x – 4320 = 0
⇔ x2 + 6x – 1080 = 0
Suy ra chiều dài mảnh đất đó là 30m, chiều rộng mảnh đất là
Vậy chiều dài mảnh đất đó là 30m, chiều rộng mảnh đất là 24m.
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 4
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Câu 1 (2 điểm): Cho biểu thức
a) Xác định a, b để biểu thức có nghĩa và hãy rút gọn P
b) Tìm giá trị của P khi
Câu 2 (2,0 điểm):
a) Cho hệ phương trình
Tìm m để hệ có nghiệm (x; y) thỏa mãn:
b) Giải phương trình:
Câu 3 ( 2,0 điểm): Một ô tô đi quãng đường dài 80km trong thời gian đã định. Ba phần tư quãng, đường đầu ô tô chạy với vận tốc nhanh hơn dự định là 10km/h, quãng đường còn lại ô tô chạy chậm hơn dự định 15km/h. Thời gian oto dự định đi hết quãng đường AB?
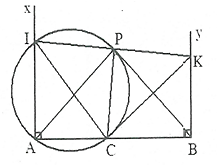
Câu 4 (3,5 điểm): Cho C là một điểm nằm trên đoạn thẳng AB (). Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, kẻ hai tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm I khác A, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắ tia IK tại P
a) Chứng minh tứ giác CPKB nội tiếp được đường tròn. Xác định tâm và bán kính của đường tròn đó.
b) Chứng minh AI.BK = AC.BC
c) Chứng minh APB vuông.
d) Cho A, B, I cố định. Tìm vị trí điểm C để diện tích tứ giác ABKI đạt giá trị lớn nhất.
Câu 5 (0,5 điểm): Tìm x, y nguyên dương thỏa mãn
----------HẾT---------
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
a) Điều kiện:
|
0,5 điểm
0,5 điểm
0,25 điểm |
|
b) Ta có:
( Thỏa mãn ) Vậy
|
0,5 điểm 0,5 điểm |
|
|
Câu 2 (2,0 điểm) |
a. Từ phương trình (1), suy ra: (3) Thay vào phương trình (2) ta được:
Thay vào (3), ta được x = m Do đó Vậy với thì hệ phương trình có nghiệm (x,y) thỏa mãn . |
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm |
|
b) Xét phương trình: Điều kiện xác định:
Đặt (4), suy ra Phương trình đã cho trở thành:
Với
Với
Vậy |
0,25 điểm
0,5 điểm
0,25 điểm
|
|
|
Câu 3 (2,0 điểm) |
Gọi vận tốc dự định đi của ô tô là x (km/h) (x > 15) Ba phần tư quãng đường đầu là: (km) Vận tốc của oto trong ba phần tư quãng đường đầu là: x + 10 (km/h) Thời gian oto đi ba phần tư quãng đường đầu là: (h) Quãng đường còn lại là: 80 – 60 = 20 (km) Vận tốc của oto trong quãng đường còn lại là: x – 15 (km/h) Thời gian oto đi hết quãng đường còn lại là: (h) Theo đầu bài, ta có phương trình: Giải phương trình trên, ta được: x = 40 Vậy thời gian ô tô đi hết quãng đường là 2 giờ. |
0,25 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,25 điểm |
|
Câu 4 (3,5 điểm) |
- Vẽ hình đúng
a) Do P thuộc đường tròn đường kính IC nên (góc nội tiếp chắn nửa đường tròn) nên tứ giác CPKB nội tiếp đường tròn đường kính CK. Tâm đường tròn này là trung điểm của CK |
0,5 điểm
0,5 điểm 0,5 điểm |
|
b) Vì nên Suy ra: Do đó: (g-g) Suy ra: |
0,25 điểm 0,5 điểm 0,25 điểm |
|
|
c) Xét đường tròn đường kính IC Ta có: (hai góc nội tiếp cùng chắn cung CP) Xét đường tròn ngoại tiếp tứ giác CPKB, ta có: (hai góc nội tiếp cùng chắn cung CP) nên Vậy vuông |
0,25 điểm
0,25 điểm |
|
|
d) Ta có: Vì AB, AI không đổi nên lớn nhất lớn nhất lớn nhất (vì theo câu 1b)) (vì không đổi). Vậy lớn nhất khi C là trung điểm AB. |
0,25 điểm
0,25 điểm |
|
|
Câu 5 (0,5 điểm) |
Từ => 1003x = 2008 - 2y Vì 2008 – 2y là một số chẵn, 1003 là một số lẻ nên x chẵn và 1003x < 1008 => x < => x = 2 => y = 1 |
0,25 điểm
0,25 điểm |
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 5
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Câu 1 (2.0 điểm):
Cho biểu thức và với ,
1. Tính giá trị biểu thức B khi x=16.
2. Biết P = A+B. Chứng minh
3. Tìm x, để .
Bài 2 (2,0 điểm):
1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một đoàn xe vận tải dự định sử dụng một số xe cùng loại để chuyên chở 90 tấn thiết bị y tế. Để đáp ứng kịp nhu cầu phục vụ công tác phòng chống dịch Covid – 19 đoàn được bổ sung thêm 5 chiếc xe cùng loại. Do đó mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn. Biết khối lượng hàng mỗi xe chuyên chở như nhau, hỏi ban đầu đoàn xe có bao nhiêu chiếc?
2. Một lọ thuốc hình trụ có chiều cao 10cm và bán kính đáy 5cm. Nhà sản xuất phủ kín mặt xung quanh của lọ thuốc bằng giấy in các thông tin về loại thuốc ấy. Hãy tính diện tích giấy cần dùng của lọ thuốc đó (cho biết độ dày của giấy in và lọ thuốc không đáng kể)?
Câu 3 (2,0 điểm):
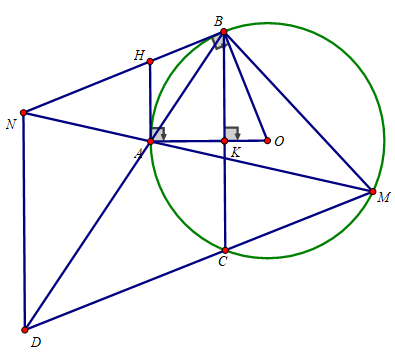
1. Giải hệ phương trình:
2. Cho phương trình: (m là tham số)
a. Giải phương trình khi m=−5
b. Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện .
Câu 4 (3,5 điểm):
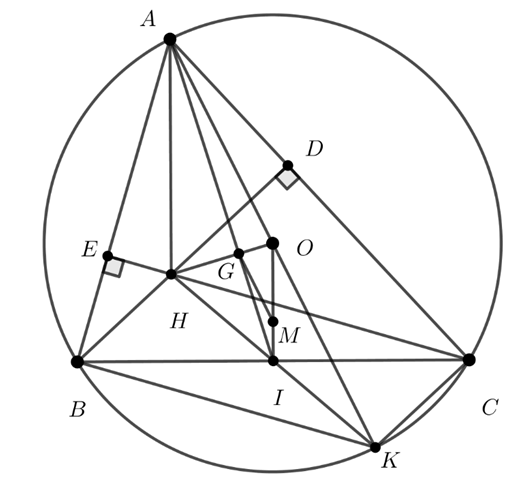
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R). Các đường cao BD và CE cắt nhau tại H.
1. Chứng minh ADHE là tứ giác nội tiếp
2. Kẻ đường kính AK. Chứng minh CK//BH và tứ giác BHCK là hình bình hành.
3. Gọi I là trung điểm của BC, G là giao điểm của AI và OH.
a. Chứng minh G là trọng tâm ΔAHK.
b. Cho B, C cố định, khi A di động trên cung lớn BC sao cho ΔABC có 3 góc nhọn thì G chuyển động trên đường nào? Tại sao?
Câu 5 (3 điểm):
Cho các số thực x,y thỏa mãn . Tìm giá trị lớn nhất và nhỏ nhất của biểu thức A=
----------HẾT---------
|
Câu |
Đáp án và hướng dẫn chấm |
Biểu điểm |
|
Câu 1 (2,0 điểm) |
1. Thay x = 16 vào biểu thức B, ta được: Vậy với x = 16 thì B = 1. |
0,25 điểm 0,25 điểm |
|
|
2. Xét biểu thức: |
0,25 điểm 0,25 điểm
0,25 điểm
0,25 điểm |
|
|
c) Xét hiệu:
Vì với mọi x với mọi x Do đó để hay khi Kết hợp với điều kiện , ta được: Vậy với |
0,25 điểm
0,25 điểm |
|
Câu 2 (2,0 điểm) |
1. Gọi số xe ban đầu của đoàn là x (xe) Theo dự định, mỗi xe chở số thiết bị y tế là: (tấn) Thực tế được bổ sung thêm 5 xe nên tổng số xe là x+5 xe Khi đó mỗi xe phải chở số thiết bị y tế là: (tấn) Vì mỗi xe chở ít hơn dự định ban đầu là 0,2 tấn nên ta có phương trình:
Vậy ban đầu đoàn có 45 xe. |
0,25 điểm
0,5 điểm
0,5 điểm)
0,25 điểm |
|
|
2. Diện tích giấy cần dùng là diện tích xung quanh của hình trụ có chiều cao 10cm và bán kính đáy 5cm. Ta có: Vậy diện tích giấy cần dùng là: |
0,25 điểm 0,25 điểm |
|
Câu 3 (2,0 điểm) |
1. Điều kiện Đặt và Khi đó hệ phương trình đã cho tương đương với:
Vậy hệ phương trình đã cho có một nghiệm duy nhất: |
0,25 điểm
0,25 điểm 0,25 điểm
0,25 điểm
|
|
|
2. Cho phương trình: (1) a. Thay m = - 5 vào phương trình (1), ta được:
Vậy tập nghiệm của phương trình đã cho là: b. Ta có: Gọi là hai nghiệm phân biệt của phương trình (1). Theo định lý Vi – et, ta có: Theo đầu bài ta có nên ta có hệ phương trình:
Thay vào biểu thức ta được: (thỏa mãn) Vậy với thì phương trình đã cho có hai nghiệm phân biệt thỏa mãn |
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm |
|
Câu 4 (3,5 điểm) |
- Vẽ hình đúng
1. Chứng minh ADHE là tứ giác nội tiếp Ta có: BD⊥ACB nên CE⊥AB nên Tứ giác ADHE có: Do đó ADHE là tứ giác nội tiếp (Tứ giác có hai góc đối có tổng bằng 180o là tứ giác nội tiếp) (đpcm). |
0,5 điểm
0,25 điểm
0,25 điểm |
|
2. Kẻ đường kính AK. Chứng minh CK//BHCK//BH và tứ giác BHCK là hình bình hành Ta có: BD⊥AC => BH⊥AC => BH⊥AC (1) AK là đường kính nên (góc nội tiếp chắn nửa đường tròn) => CK⊥AC (2) Từ (1) và (2) suy ra BH//CK (cùng vuông góc với AC) (đpcm). Lại có AK là đường kính nên (góc nội tiếp chắn nửa đường tròn) => BK⊥AB Mà CE⊥AB => CH⊥AB. Do đó BK//CH (cùng vuông góc với AB) Tứ giác BHCK có BH//KC, BK//CH nên là hình bình hành (tứ giác có hai cặp đối song song là hình bình hành). (đpcm) |
0,25 điểm
0,25 điểm 0,25 điểm
0,25 điểm |
|
|
3. a. Chứng minh G là trọng tâm ΔAHK Tứ giác BHCK là hình bình hành (cmt) nên I là trung điểm BC cũng là trung điểm của HK (tính chất) AK là đường kính nên O là trung điểm của AK. Xét tam giác AHK có G là giao điểm hai đường trung tuyến AI và HO nên G là trọng tâm tam giác. (đpcm) b. Qua G kẻ đường thẳng song song với OA cắt OI tại M. Kẻ GM //AO nên theo định lí Ta-let ta có: Mà G là trọng tâm tam giác AHK nên: Do đó Vì B, C và O cố định nên I cố định, hơn nữa nên M cố định. Ta lại có: Do đó,G luôn cách M một khoảng cố định Khi đó G nằm trên đường tròn (M, ) Vậy khi A di động trên cung lớn BC sao cho ΔABC có 3 góc nhọn thì G chuyển động trên đường tròn tâm M bán kính . |
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
|
|
|
Câu 5 (0,5 điểm) |
Ta có: Vì với mọi y với mọi y
TH1: Ta có: Vì Do đó GTNN của A là 1 khi và GTLN của A là 9 khi TH2: Vậy GTNN của A là 1 khi và GTLN của A là 9 khi . |
0,25 điểm
0,25 điểm |
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 6
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Câu 1 (2.0 điểm): Cho biểu thức với
1) Rút gọn biểu thức A
2) Tìm x để
3) Tìm x để
Câu 2 (2,0 điểm):
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một ô tô đi từ A tới B cách nhau 420km với vận tốc dự định. Khi đi được 120 km thì ô tô tăng tốc thêm 15 km/h và đi hết quãng đường còn lại với vận tốc mới. Tính vận tốc ban đầu của ô tô, biết thời gian đi hết quãng đường AB là 6 giờ.
Câu 3 (2,0 điểm):
1) Giải hệ phương trình:
2) Cho phương trình:
a) Giải phương trình khi m = 2.
b) Tìm m để phương trình có hai nghiệm phân biệt sao cho
Câu 4 (3,5 điểm):
Từ điểm M nằm bên ngoài đường tròn (O), kẻ hai tiếp tuyến MA, MB với đường tròn (O) và A, B là các tiếp điểm. Gọi E là trung điểm của đoạn thẳng MB; C là giao điểm của AE và đường tròn (O), ( C khác A). H là giao điểm của AB và MO.
1) Chứng minh 4 điểm M, A, O, B cùng thuộc một đường tròn
2) Chứng minh rằng .
3) Chứng minh tứ giác HCEB là tứ giác nội tiếp
4) Gọi D là giao điểm của MC và đường tròn (O) (D khác C). Chứng minh là tam giác cân.
Câu 5: (0,5 điểm) Tìm cặp số (a, b) thỏa mãn và
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 7
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 90 phút
Câu 1: Cho hàm số y = -3x2. Kết luận nào sau đây là đúng :
A. Hàm số trên luôn đồng biến
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0, nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0, nghịch biến khi x > 0
Câu 2: Cho phương trình bậc hai x2 – 2(m + 1) x + 4m = 0. Phương trình có nghiệm kép khi m bằng:
A. 1 C. Với mọi m
B. –1 D. Một kết quả khác
Câu 3: Cung AB của đường tròn (O; R) có số đo là 60o. Khi đó diện tích hình quạt AOB là:
Câu 4: Tứ giác MNPQ nội tiếp đường tròn khi:
A.∠(MNP) + ∠(NPQ) = 180o
B.∠(MNP) = ∠(MPQ)
C. MNPQ là hình thang cân
D. MNPQ là hình thoi
Phần tự luận (8 điểm)
Bài 1 (2,0 điểm)
1) Tìm điều kiện xác định của biểu thức
2) Cho biểu thức 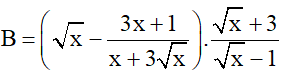
a) Rút gọn biểu thức B
b) Tìm giá trị nhỏ nhất của P = A.B với x > 1
Bài 2 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một tấm bìa hình chữ nhật có chiều dài hơn chiều rộng 3dm. Nếu giảm chiều rộng đi 1dm và tăng chiều dài thêm 1dm thì diện tích tấm bìa là 66 Tính chiều rộng và chiều dài của tấm bìa lúc ban đầu.
Bài 3 (2,0 điểm)
1) Cho phương trình x4 + mx2 - m - 1 = 0(m là tham số)
a) Giải phương trình khi m = 2
b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.
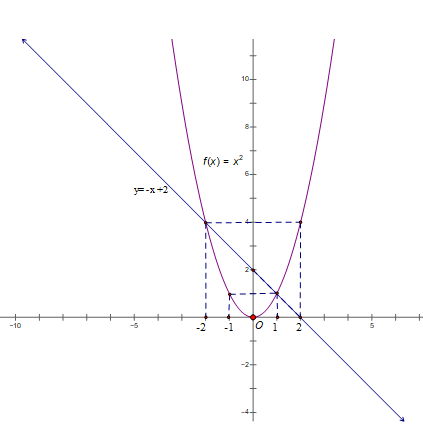
2) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2 và đường thẳng (d): y = 2x + m (m là tham số).
a) Xác định m để đường thẳng (d) tiếp xúc với parabol (P). Tìm hoành độ tiếp điểm.
b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).
Bài 4 (3,5 điểm) Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.
a) Chứng minh tứ giác AFEB là tứ giác nội tiếp
b) Chứng minh CF.CB = CE.CA
c) Nếu dây AB có độ dài bằng R√3 , hãy tính số đo của (ACB)
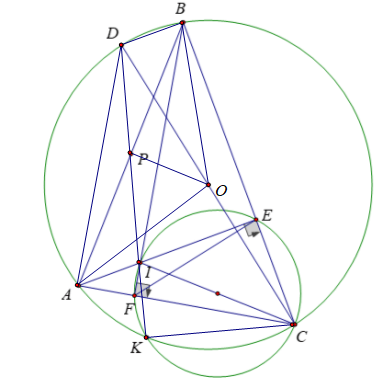
d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.
Hướng dẫn giải
Phần trắc nghiệm (2 điểm)
| 1.D | 2.A | 3.B | 4.C |
Phần tự luận (8 điểm)
Bài 1
Biểu thức A xác định khi √x - 1 ≠ 0 ⇔ √x ≠ 1 ⇔ x ≠ 1
Vậy GTNN của P là 2√3 + 3 đạt được khi x = 4 + 2√3
Bài 2
Gọi chiều dài của tấm bìa là x (x > 3) (dm)
⇒ Chiều rộng của tấm bìa là x – 3 (dm)
Nếu tăng chiều dài 1 dm và giảm chiều rộng 1 dm thì diện tích là 66 dm2 nên ta có phương trình:
(x + 1)(x – 3 – 1) = 66
⇔ (x + 1)(x – 4 ) = 66
⇔ x2 – 3x – 4 – 66 = 0
⇔ x2 – 3x – 70 = 0
Δ = 32 - 4.(-70) = 289 ⇒ √Δ = 17
⇒ Phương trình đã cho có 2 nghiệm
Do x > 3 nên x =10
Vậy chiều dài của tấm bìa là 10 dm
Chiều rộng của tấm bìa là 7 dm.
Bài 3
1) x4 + mx2 - m - 1 = 0
a) Khi m = 2, phương trình trở thành: x4 + 2x2 – 3 = 0
Đặt x2 = t (t ≥ 0). Khi đó ta có phương trình: t2 + 2t - 3 = 0
⇒ Phương trình có nghiệm t = 1 và t = -3 (do phương trình có dạng a + b + c = 0)
Do t ≥ 0 nên t = 1 ⇒ x2 = 1 ⇒ x = ±1
b) Đặt x2 = t (t ≥ 0). Khi đó ta có phương trình: t2 – mt – m – 1 = 0 (*)
Δ = m2 - 4(-m - 1) = m2 + 4m + 4 = (m + 2)2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
2) parabol (P): y = x2 ; đường thẳng (d): y = 2x + m (m là tham số).
a) phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2x + m ⇔ x2 - 2x - m = 0
Δ'= 1 + m
(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm
⇔ Δ'= 1 + m = 0 ⇔ m = -1
Khi đó hoành độ giao điểm là x = 1
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
Khi đó 2 nghiệm của phương trình là:
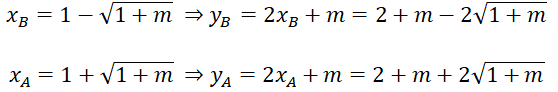
Kẻ BB' ⊥ OM ; AA' ⊥ OM
Ta có:
SAOM = 1/2 AA'.OM ; SBOM = 1/2 BB'.OM
Theo bài ra:
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
Bài 4
a) Xét tứ giác AEFB có:
∠(AFB) = 90o ( AF là đường cao)
∠(AEB) = 90o ( BE là đường cao)
⇒ 2 đỉnh E và F cùng nhìn cạnh AB dưới 1 góc bằng nhau
⇒ AEFB là tứ giác nội tiếp.
b) Xét ΔBEC và ΔAFC có:
∠(BCA) là góc chung
∠(BEC) = ∠(AFC) = 90 o
⇒ ΔBEC ∼ ΔAFC
c) Gọi P là trung điểm của AB
Do tam giác OAB cân tại O nên OP ⊥ AB
Tam giác OAP vuông tại P có:
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 8
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Phần trắc nghiệm (2 điểm)
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn:
A. 2x2 - 3x + 1 = 0 B.-2x = 4
C. 2x + 3y = 7 D. 1/x + y = 3
Câu 2: Hệ phương trình 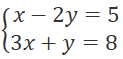
A. (-3; -1) B. (3; 1)
C. (3; -1) D. (1; -3)
Câu 3: Cho AB là dây cung của đường tròn (O; 4 cm), biết AB = 4 cm, số đo của cung nhỏ AB là:
A. 60o B. 120o C. 30o D. 90o
Câu 4: Bán kính hình tròn nội tiếp hình vuông cạnh 2 cm là:
A.2 cm B.√2 cm C.1 cm D.4 cm
Phần tự luận (8 điểm)
Bài 1 (1, 5 điểm) giải phương trình và hệ phương trình sau:
a) x2 - 7x + 5 = 0
Bài 2 (1, 5 điểm) Cho hai hàm số : y = x2 (P) và y = - x + 2 (d)
a) Vẽ 2 đồ thì hàm số trên cùng 1 hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d)
c) Viết phương trình đường thẳng d' song song với d và cắt (P) tại điểm có hoành độ -1.
Bài 3 (1, 5 điểm) Cho phương trình x2 + (m – 2)x – m + 1 =0
a) Tìm m để phương trình có 1 nghiệm x = 2. Tìm nghiệm còn lại
b) Chứng minh rằng phương trình luôn có nghiệm với mọi m
c) Tìm giá trị nhỏ nhất của biểu thức A = x12 + x22 -6x1 x2
Bài 4 (3,5 điểm) Cho (O;OA), dây BC vuông góc với OA tại K. Kẻ tiếp tuyến của (O) tại B và A, hai tiếp tuyến này cắt nhau tại H
a) Chứng minh tứ giác OBHA nội tiếp được đường tròn
b) Lấy trên O điểm M (M khác phía với A so với dây BC, dây BM lớn hơn dây MC). Tia MA và BH cắt nhau tại N. chứng minh ∠(NMC) = ∠(BAH)
c) Tia MC và BA cắt nhau tại D. Chứng minh tứ giác MBND nội tiếp được đường tròn.
d) Chứng minh OA ⊥ ND
Hướng dẫn giải
Phần trắc nghiệm (2 điểm)
| 1.C | 2.C | 3.A | 4.B |
Câu 4: Chọn đáp án C
Kẻ OH ⊥ AB. Do ABCD là hình vuông nên ∠OAH = 45o
Tam giác ABC vuông tại B có: AC2 = AB2 + BC2 = 22 + 22 = 8
Nên AC = 2√2cm
Vì O là trung điểm AC nên
Xét tam giác OAH vuông tại H có:
Vậy bán kính đường tròn nội tiếp hình vuông cạnh 2cm là 1cm
Phần tự luận (8 điểm)
Bài 1
a) x2 - 7x + 5 = 0
Δ = 72 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
Vậy hệ phương trình đã cho có tập nghiệm
Vậy hệ phương trình đã cho có nghiệm (x; y) = (0; 3)
Bài 2
a) Xét hàm số: y = x2 (P)
Tập xác định R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
Xét hàm số: y = - x + 2 (d)
Tập xác định R
Bảng giá trị
| x | 0 | 2 |
| y = - x + 2 | 2 | 0 |
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = -x + 2 ⇔ x2 + x - 2 = 0
⇒ Phương trình có nghiệm 1 và -2 ( phương trình dạng a + b + c = 0)
Với x = 1 ⇒ y = x2 = 1
Với x = - 2 ⇒ y = x2 = 4
Vậy tọa độ giao điểm của (P) và (d) là (1; 1) và (-2; 4)
c) Do d' // d nên phương trình của d' có dạng: y = -x + b (b ≠ 2)
Gọi A là giao điểm của d' và (P). A có hoành độ -1 ⇒ tung độ của A là 1
Do A (-1; 1) nên tọa độ của A thỏa mãn phương trình đường thẳng d'
⇒ 1 = -(-1) + b ⇒ b = 0
⇒ Phương trình đường thẳng d' là y = -x.
Bài 3 x2 + (m – 2)x – m + 1 = 0
a) phương trình có 1 nghiệm x = 2 nên :
22 + (m-2).2 - m + 1 = 0
⇔ m = -1
Với m = -1, phương trình trở thành: x2 – 3x + 2 = 0
Theo hệ thức Vi-et ta có: x1 + x2 = 3
Giả sử x1 = 2 ⇒ x2 = 1
Vậy với m = - 1 thì phương trình có 1 nghiệm là 2 và nghiệm còn lại là 1.
b) Δ = (m - 2)2 -4.(-m + 1) = m2 - 4m + 4 + 4m - 4 = m2 ≥ 0 ∀ m
⇒ Phương trình đã cho luôn có nghiệm với mọi m
c) Theo hệ thức Vi- et ta có:
A = x12 + x22 -6x1 x2 = (x1 + x2 )2 - 8x1 x2
= (2 - m)2 - 8(-m + 1) = m2 - 4m + 4 + 8m - 8
= m2 + 4m - 4 = (m + 2)2 - 8
Ta có: (m + 2)2 ≥ 0 ∀ m
⇒ (m + 2)2 - 8 ≥ -8 ∀ m ⇔ A ≥ -8 ∀ m
Dấu bằng xảy ra khi (m + 2)2 = 0 ⇔ m= -2
Vậy GTNN của A là -8, đạt được khi m = -2
Bài 4
a) Xét tứ giác OBHA có:
∠(OBH) = 90o ( BH là tiếp tuyến của (O)
∠(OAH) = 90o (AH là tiếp tuyến của (O)
⇒ ∠(OBH) + ∠(OAH) = 180o
⇒ Tứ giác OBHA là tứ giác nội tiếp
b) Ta có: Một phần đường kính OA vuông góc dây BC
⇒ AB = AC ⇒ sđ cung AB = sđ cung AC
⇒ ∠(BAH) = ∠(ABC) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn 2 cung bằng nhau)
Tứ giác ABMC nội tiếp (O)
⇒ ∠(NMC) = ∠(ABC) (2 góc nội tiếp cùng chắn cung AC)
Do đó: ∠(NMC) = ∠(BAH)
c) 2 tiếp tuyến HA và HB cắt nhau tại H
⇒ ΔHAB cân tại H ⇒ ∠(BAH) = ∠(HBA)
Theo ý b) ∠(NMC) = ∠(BAH)
⇒ ∠(NMC) = ∠(HBA)
Xét tứ giác MBND có: ∠(NMC) = ∠(HBA)
⇒ 2 đỉnh M và B cùng nhìn cạnh ND dưới 1 góc bằng nhau
⇒ MBND là tứ giác nội tiếp.
d) Xét tứ giác MBND nội tiếp có:
∠(BDN) = ∠(BMN) (2 góc nội tiếp cùng chắn cung BN)
Xét tứ giác ABMC nội tiếp (O) có:
∠(ABC) = ∠(BMN) (2 góc nội tiếp cùng chắn cung bằng nhau )
⇒ ∠(BDN) = ∠(ABC)
Mà 2 góc này ở vị trí so le trong
⇒ ND // BC
Mà BC ⊥ OA ⇒ ND ⊥ OA
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 9
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1: (1,5 điểm) Giải phương trình và hệ phương trình
a) 2x2 - 3x + 1 = 0
b) x3 - 3x2 + 2 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y = x2
b) Tìm m để đường thẳng (d) : y = 2x + m tiếp xúc với (P).
Bài 3: (1,5 điểm) Cho phương trình (ấn số x): x2 – 4x + m – 2 = 0 (1)
a) Giá trị nào của m thì phương trình (1) có nghiệm
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn 3x1 – x2 = 8
Bài 4: (1 điểm) Một ô tô đi từ A đến B với một vận tốc xác định. Nếu vận tốc tăng thêm 30 km/h thì thời gian đi sẽ giảm 1 giờ. Nếu vận tốc giảm bớt 15 km/h thì thời gian đi tăng thêm 1 giờ. Tính vận tốc và thời gian đi từ A đến B của ô tô.
Bài 5: (3,5 điểm) Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.
b) Chứng minh BE.BA = BI.BC
c) Chứng minh tứ giác OIED nội tiếp.
d) Cho biết BC = 16cm. Tính BE.BA + CD.CA
Đáp án và Hướng dẫn giải
Bài 1:
a) 2x2 - 3x + 1 = 0
a = 2; b = - 3; c = 1 ⇒ a + b + c = 0
Do đó phương trình có nghiệm x1 = 1; x2 = 1/2
b) x3 - 3x2 + 2 = 0
⇔ x3 - x2 - 2x2 + 2 = 0
⇔ x2(x - 1) - 2(x2 - 1) = 0
⇔ x2(x - 1) - 2(x + 1)(x - 1) = 0
⇔ (x - 1)[x2 - 2(x + 1)] = 0
⇔ (x - 1)(x2 - 2x - 2) = 0
* Ta có: x - 1 = 0 khi x = 1
* Xét x2 – 2x - 2 = 0 (*)
Có ∆' = (-1)2 - 1(-2) = 3 > 0 nên phương trình (*) có 2 nghiệm phân biệt:
x1 = 1 + √3; x2 = 1 - √3
Vậy phương trình đã cho có tập nghiệm là S = {1 - √3; 1; 1 + √3}
Khi đó hệ phương trình trở thành:
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Phương trình hoành độ giao điểm của (P) và (d) là x2 = 2x + m ⇔ x2 - 2x - m = 0
Δ' = 1-(-m) = 1 + m
(d) tiếp xúc với (P) khi và chỉ khi phương trình hoành độ giao điểm của (P) và d có một nghiệm duy nhất
⇔ Δ' = 0 ⇔ 1 + m = 0 ⇔ m = -1
Vậy với m = -1 thì d tiếp xúc với (P)
Bài 3:
a) Δ' = 22 - (m - 2) = 6 - m
Phương trình đã cho có nghiệm khi và chỉ khi Δ' ≥ 0
⇔ 6 - m ≥ 0 ⇔ m ≤ 6
Vậy với m ≤ 6 thì phương trình đã cho có nghiệm
b) Theo hệ thức Vi-et ta có:
Theo bài ra:
3x1 - x2 = 8
⇔ 3x1 - x2 = 2(x1 + x2)
⇔ x1 = 3x2
Khi đó: x1 + x2 = 4 ⇔ 3x2 + x2 = 4 ⇔ 4x2 = 4 ⇔ x2 = 1
⇒ x1 = 3
⇒ x1 x2 = 3 ⇒ m - 2 = 3 ⇔ m = 5
Vậy với m = 5 thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
Bài 4:
Gọi vận tốc dự định của ô tô là x (km/h) (x > 15)
Thời gian dự định đi của ô tô là y (h) (y > 1)
⇒ Quãng đường AB là xy (km)
Nếu vận tốc tăng 30 km/h thì thời gian giảm đi 1h nên ta có phương trình:
(x + 30)(y - 1) = xy ⇔ -x + 30y = 30 (1)
Nếu vận tốc giảm 15 km/h thì thời gian tăng 1h nên ta có phương trình
(x - 15)(y + 1) = xy ⇔ x - 15y = 15 (2)
Từ (1) và (2) ta có hệ phương trình:
Vậy vận tốc đi từ A đến B là 60 km/h
Thời gian đi từ A đến B là 3h.
Bài 5:
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90o (hai góc nội tiếp chắn nửa đườn tròn)
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = BC2 = 162 = 256
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 10
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 3x2 – 7x + 2 = 0
b) x4 – 5x + 4 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y= x2/4
b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B
Bài 3: (1,5 điểm) Cho phương trình (ẩn x) : x2 – 2mx – 4m – 4 = 0(1)
a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x12 + x22 - x1x2 = 13
Bài 4: (1 điểm) Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2.
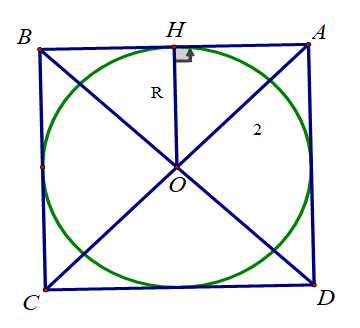
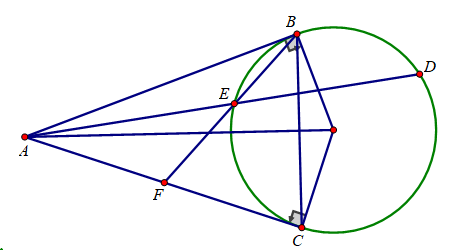
Bài 5: (3,5 điểm) Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
Đáp án và Hướng dẫn giải
Bài 1:
a) 3x2 – 7x + 2 = 0
Δ= 72 -4.3.2 = 49 - 24 = 25 > 0 ⇒ √Δ = 5
Phương trình có 2 nghiệm phân biệt:
Vậy tập nghiệm của phương trình là S = {2; 1/3}
b) x4 - 5x2 + 4 = 0
Đặt t = x2 ≥ 0 , ta có phương trình:
t2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t1 = 1 (nhận) ; t2 = 4 (nhận)
với t = 1 ⇔ x2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
Vậy hệ phương trình có nghiệm (x; y) = ( √5; -1)
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = x2 / 4 | 4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số y = x2 / 4 là một đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Với x = 4, ta có: y = x2/4 = 4 ⇒ A (4; 4)
Với x = 2, ta có y = x2/4 = 1 ⇒ B ( 2; 1)
Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b
Đường thẳng đi qua A (4; 4) nên 4 = 4a + b
Đường thẳng đi qua B (2; 1) nên : 1= 2a + b
Ta có hệ phương trình
Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2
Bài 3:
a) Δ' = m2 - (-4m - 4) = m2 + 4m + 4 = (m + 2)2 ≥ 0 ∀m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Gọi x1 ; x2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
x12 + x22 -x1 x2 = (x1 + x2 )2 - 3x1 x2 = 4m2 + 3(4m + 4)
Theo bài ra: x12 + x22 - x1 x2=13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
Δm = 122 -4.4.(-1) = 160 ⇒ √(Δm ) = 4√10
Phương trình có 2 nghiệm phân biệt
Vậy với 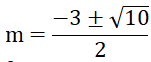
Bài 4:
Gọi chiều rộng của hình chữ nhật là x (m) ( x > 0 )
⇒ Chiều dài của hình chữ nhật là x + 3 (m)
Khi đó diện tích của hình chữ nhật là x(x + 3) (m2 )
Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2 nên ta có phương trình:
(x + 2)(x + 3 + 2) = x(x + 3) + 70
⇔ (x + 2)(x + 5) = x(x + 3) + 70
⇔ x2 + 7x + 10 = x2 + 3x + 70
⇔ 4x = 60
⇔ x = 15
Vậy chiều rộng của hình chữ nhật là 15m
Chiều dài của hình chữ nhật là 18m
Bài 5:


Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 11
Phần trắc nghiệm (2 điểm)
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn:
A. 2x2 - 3x + 1 = 0 B.-2x = 4
C. 2x + 3y = 7 D. 1/x + y = 3
Câu 2: Hệ phương trình 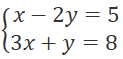
A. (-3; -1) B. (3; 1)
C. (3; -1) D. (1; -3)
Câu 3: Cho AB là dây cung của đường tròn (O; 4 cm), biết AB = 4 cm, số đo của cung nhỏ AB là:
A. 60o B. 120o C. 30o D. 90o
Câu 4: Bán kính hình tròn nội tiếp hình vuông cạnh 2 cm là:
A.2 cm B.√2 cm C.1 cm D.4 cm
Phần tự luận (8 điểm)
Bài 1 (1, 5 điểm) giải phương trình và hệ phương trình sau:
a) x2 - 7x + 5 = 0
Bài 2 (1, 5 điểm) Cho hai hàm số : y = x2 (P) và y = - x + 2 (d)
a) Vẽ 2 đồ thì hàm số trên cùng 1 hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d)
c) Viết phương trình đường thẳng d' song song với d và cắt (P) tại điểm có hoành độ -1.
Bài 3 (1, 5 điểm) Cho phương trình x2 + (m – 2)x – m + 1 =0
a) Tìm m để phương trình có 1 nghiệm x = 2. Tìm nghiệm còn lại
b) Chứng minh rằng phương trình luôn có nghiệm với mọi m
c) Tìm giá trị nhỏ nhất của biểu thức A = x12 + x22 -6x1 x2
Bài 4 (3,5 điểm) Cho (O;OA), dây BC vuông góc với OA tại K. Kẻ tiếp tuyến của (O) tại B và A, hai tiếp tuyến này cắt nhau tại H
a) Chứng minh tứ giác OBHA nội tiếp được đường tròn
b) Lấy trên O điểm M (M khác phía với A so với dây BC, dây BM lớn hơn dây MC). Tia MA và BH cắt nhau tại N. chứng minh ∠(NMC) = ∠(BAH)
c) Tia MC và BA cắt nhau tại D. Chứng minh tứ giác MBND nội tiếp được đường tròn.
d) Chứng minh OA ⊥ ND
ĐÁP ÁN
Phần trắc nghiệm (2 điểm)
| 1.C | 2.C | 3.A | 4.B |
Câu 4: Chọn đáp án C
Kẻ OH ⊥ AB. Do ABCD là hình vuông nên ∠OAH = 45o
Tam giác ABC vuông tại B có: AC2 = AB2 + BC2 = 22 + 22 = 8
Nên AC = 2√2cm
Vì O là trung điểm AC nên
Xét tam giác OAH vuông tại H có:
Vậy bán kính đường tròn nội tiếp hình vuông cạnh 2cm là 1cm
Phần tự luận (8 điểm)
Bài 1
a) x2 - 7x + 5 = 0
Δ = 72 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
Vậy hệ phương trình đã cho có tập nghiệm
Vậy hệ phương trình đã cho có nghiệm (x; y) = (0; 3)
Bài 2
a) Xét hàm số: y = x2 (P)
Tập xác định R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
Xét hàm số: y = - x + 2 (d)
Tập xác định R
Bảng giá trị
| x | 0 | 2 |
| y = - x + 2 | 2 | 0 |
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = -x + 2 ⇔ x2 + x - 2 = 0
⇒ Phương trình có nghiệm 1 và -2 ( phương trình dạng a + b + c = 0)
Với x = 1 ⇒ y = x2 = 1
Với x = - 2 ⇒ y = x2 = 4
Vậy tọa độ giao điểm của (P) và (d) là (1; 1) và (-2; 4)
c) Do d' // d nên phương trình của d' có dạng: y = -x + b (b ≠ 2)
Gọi A là giao điểm của d' và (P). A có hoành độ -1 ⇒ tung độ của A là 1
Do A (-1; 1) nên tọa độ của A thỏa mãn phương trình đường thẳng d'
⇒ 1 = -(-1) + b ⇒ b = 0
⇒ Phương trình đường thẳng d' là y = -x.
Bài 3 x2 + (m – 2)x – m + 1 = 0
a) phương trình có 1 nghiệm x = 2 nên :
22 + (m-2).2 - m + 1 = 0
⇔ m = -1
Với m = -1, phương trình trở thành: x2 – 3x + 2 = 0
Theo hệ thức Vi-et ta có: x1 + x2 = 3
Giả sử x1 = 2 ⇒ x2 = 1
Vậy với m = - 1 thì phương trình có 1 nghiệm là 2 và nghiệm còn lại là 1.
b) Δ = (m - 2)2 -4.(-m + 1) = m2 - 4m + 4 + 4m - 4 = m2 ≥ 0 ∀ m
⇒ Phương trình đã cho luôn có nghiệm với mọi m
c) Theo hệ thức Vi- et ta có:
A = x12 + x22 -6x1 x2 = (x1 + x2 )2 - 8x1 x2
= (2 - m)2 - 8(-m + 1) = m2 - 4m + 4 + 8m - 8
= m2 + 4m - 4 = (m + 2)2 - 8
Ta có: (m + 2)2 ≥ 0 ∀ m
⇒ (m + 2)2 - 8 ≥ -8 ∀ m ⇔ A ≥ -8 ∀ m
Dấu bằng xảy ra khi (m + 2)2 = 0 ⇔ m= -2
Vậy GTNN của A là -8, đạt được khi m = -2
Bài 4
a) Xét tứ giác OBHA có:
∠(OBH) = 90o ( BH là tiếp tuyến của (O)
∠(OAH) = 90o (AH là tiếp tuyến của (O)
⇒ ∠(OBH) + ∠(OAH) = 180o
⇒ Tứ giác OBHA là tứ giác nội tiếp
b) Ta có: Một phần đường kính OA vuông góc dây BC
⇒ AB = AC ⇒ sđ cung AB = sđ cung AC
⇒ ∠(BAH) = ∠(ABC) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn 2 cung bằng nhau)
Tứ giác ABMC nội tiếp (O)
⇒ ∠(NMC) = ∠(ABC) (2 góc nội tiếp cùng chắn cung AC)
Do đó: ∠(NMC) = ∠(BAH)
c) 2 tiếp tuyến HA và HB cắt nhau tại H
⇒ ΔHAB cân tại H ⇒ ∠(BAH) = ∠(HBA)
Theo ý b) ∠(NMC) = ∠(BAH)
⇒ ∠(NMC) = ∠(HBA)
Xét tứ giác MBND có: ∠(NMC) = ∠(HBA)
⇒ 2 đỉnh M và B cùng nhìn cạnh ND dưới 1 góc bằng nhau
⇒ MBND là tứ giác nội tiếp.
d) Xét tứ giác MBND nội tiếp có:
∠(BDN) = ∠(BMN) (2 góc nội tiếp cùng chắn cung BN)
Xét tứ giác ABMC nội tiếp (O) có:
∠(ABC) = ∠(BMN) (2 góc nội tiếp cùng chắn cung bằng nhau )
⇒ ∠(BDN) = ∠(ABC)
Mà 2 góc này ở vị trí so le trong
⇒ ND // BC
Mà BC ⊥ OA ⇒ ND ⊥ OA
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 12
Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 3x2 – 7x + 2 = 0
b) x4 – 5x + 4 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y= x2/4
b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B
Bài 3: (1,5 điểm) Cho phương trình (ẩn x) : x2 – 2mx – 4m – 4 = 0(1)
a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x12 + x22 - x1x2 = 13
Bài 4: (1 điểm) Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2.
Bài 5: (3,5 điểm) Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
ĐÁP ÁN
Bài 1:
a) 3x2 – 7x + 2 = 0
Δ= 72 -4.3.2 = 49 - 24 = 25 > 0 ⇒ √Δ = 5
Phương trình có 2 nghiệm phân biệt:
Vậy tập nghiệm của phương trình là S = {2; 1/3}
b) x4 - 5x2 + 4 = 0
Đặt t = x2 ≥ 0 , ta có phương trình:
t2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t1 = 1 (nhận) ; t2 = 4 (nhận)
với t = 1 ⇔ x2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
Vậy hệ phương trình có nghiệm (x; y) = ( √5; -1)
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = x2 / 4 | 4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số y = x2 / 4 là một đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Với x = 4, ta có: y = x2/4 = 4 ⇒ A (4; 4)
Với x = 2, ta có y = x2/4 = 1 ⇒ B ( 2; 1)
Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b
Đường thẳng đi qua A (4; 4) nên 4 = 4a + b
Đường thẳng đi qua B (2; 1) nên : 1= 2a + b
Ta có hệ phương trình
Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2
Bài 3:
a) Δ' = m2 - (-4m - 4) = m2 + 4m + 4 = (m + 2)2 ≥ 0 ∀m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Gọi x1 ; x2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
x12 + x22 -x1 x2 = (x1 + x2 )2 - 3x1 x2 = 4m2 + 3(4m + 4)
Theo bài ra: x12 + x22 - x1 x2=13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
Δm = 122 -4.4.(-1) = 160 ⇒ √(Δm ) = 4√10
Phương trình có 2 nghiệm phân biệt
Vậy với thì phương trình có 2 nghiệm x1; x2 thỏa mãn điều kiện x12 + x22 - x1 x2 = 13
Bài 4:
Gọi chiều rộng của hình chữ nhật là x (m) ( x > 0 )
⇒ Chiều dài của hình chữ nhật là x + 3 (m)
Khi đó diện tích của hình chữ nhật là x(x + 3) (m2 )
Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2 nên ta có phương trình:
(x + 2)(x + 3 + 2) = x(x + 3) + 70
⇔ (x + 2)(x + 5) = x(x + 3) + 70
⇔ x2 + 7x + 10 = x2 + 3x + 70
⇔ 4x = 60
⇔ x = 15
Vậy chiều rộng của hình chữ nhật là 15m
Chiều dài của hình chữ nhật là 18m
Bài 5:


Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 13
Câu 1: Cho hàm số y = -3x2. Kết luận nào sau đây là đúng :
A. Hàm số trên luôn đồng biến
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0, nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0, nghịch biến khi x > 0
Câu 2: Cho phương trình bậc hai x2 – 2(m + 1) x + 4m = 0. Phương trình có nghiệm kép khi m bằng:
A. 1 C. Với mọi m
B. –1 D. Một kết quả khác
Câu 3: Cung AB của đường tròn (O; R) có số đo là 60o. Khi đó diện tích hình quạt AOB là:
Câu 4: Tứ giác MNPQ nội tiếp đường tròn khi:
A.∠(MNP) + ∠(NPQ) = 180o
B.∠(MNP) = ∠(MPQ)
C. MNPQ là hình thang cân
D. MNPQ là hình thoi
Phần tự luận (8 điểm)
Bài 1 (2,0 điểm)
1) Tìm điều kiện xác định của biểu thức
2) Cho biểu thức 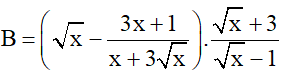
a) Rút gọn biểu thức B
b) Tìm giá trị nhỏ nhất của P = A.B với x > 1
Bài 2 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một tấm bìa hình chữ nhật có chiều dài hơn chiều rộng 3dm. Nếu giảm chiều rộng đi 1dm và tăng chiều dài thêm 1dm thì diện tích tấm bìa là 66 Tính chiều rộng và chiều dài của tấm bìa lúc ban đầu.
Bài 3 (2,0 điểm)
1) Cho phương trình x4 + mx2 - m - 1 = 0(m là tham số)
a) Giải phương trình khi m = 2
b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.
2) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2 và đường thẳng (d): y = 2x + m (m là tham số).
a) Xác định m để đường thẳng (d) tiếp xúc với parabol (P). Tìm hoành độ tiếp điểm.
b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).
Bài 4 (3,5 điểm) Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.
a) Chứng minh tứ giác AFEB là tứ giác nội tiếp
b) Chứng minh CF.CB = CE.CA
c) Nếu dây AB có độ dài bằng R√3 , hãy tính số đo của (ACB)
d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.
ĐÁP ÁN
Phần trắc nghiệm (2 điểm)
| 1.D | 2.A | 3.B | 4.C |
Phần tự luận (8 điểm)
Bài 1
Biểu thức A xác định khi √x - 1 ≠ 0 ⇔ √x ≠ 1 ⇔ x ≠ 1
Vậy GTNN của P là 2√3 + 3 đạt được khi x = 4 + 2√3
Bài 2
Gọi chiều dài của tấm bìa là x (x > 3) (dm)
⇒ Chiều rộng của tấm bìa là x – 3 (dm)
Nếu tăng chiều dài 1 dm và giảm chiều rộng 1 dm thì diện tích là 66 dm2 nên ta có phương trình:
(x + 1)(x – 3 – 1) = 66
⇔ (x + 1)(x – 4 ) = 66
⇔ x2 – 3x – 4 – 66 = 0
⇔ x2 – 3x – 70 = 0
Δ = 32 - 4.(-70) = 289 ⇒ √Δ = 17
⇒ Phương trình đã cho có 2 nghiệm
Do x > 3 nên x =10
Vậy chiều dài của tấm bìa là 10 dm
Chiều rộng của tấm bìa là 7 dm.
Bài 3
1) x4 + mx2 - m - 1 = 0
a) Khi m = 2, phương trình trở thành: x4 + 2x2 – 3 = 0
Đặt x2 = t (t ≥ 0). Khi đó ta có phương trình: t2 + 2t - 3 = 0
⇒ Phương trình có nghiệm t = 1 và t = -3 (do phương trình có dạng a + b + c = 0)
Do t ≥ 0 nên t = 1 ⇒ x2 = 1 ⇒ x = ±1
b) Đặt x2 = t (t ≥ 0). Khi đó ta có phương trình: t2 – mt – m – 1 = 0 (*)
Δ = m2 - 4(-m - 1) = m2 + 4m + 4 = (m + 2)2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
2) parabol (P): y = x2 ; đường thẳng (d): y = 2x + m (m là tham số).
a) phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2x + m ⇔ x2 - 2x - m = 0
Δ'= 1 + m
(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm
⇔ Δ'= 1 + m = 0 ⇔ m = -1
Khi đó hoành độ giao điểm là x = 1
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
Khi đó 2 nghiệm của phương trình là:
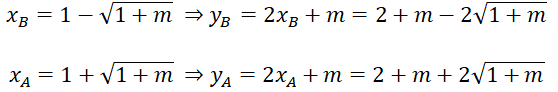
Kẻ BB' ⊥ OM ; AA' ⊥ OM
Ta có:
SAOM = 1/2 AA'.OM ; SBOM = 1/2 BB'.OM
Theo bài ra:
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
Bài 4
a) Xét tứ giác AEFB có:
∠(AFB) = 90o ( AF là đường cao)
∠(AEB) = 90o ( BE là đường cao)
⇒ 2 đỉnh E và F cùng nhìn cạnh AB dưới 1 góc bằng nhau
⇒ AEFB là tứ giác nội tiếp.
b) Xét ΔBEC và ΔAFC có:
∠(BCA) là góc chung
∠(BEC) = ∠(AFC) = 90 o
⇒ ΔBEC ∼ ΔAFC
c) Gọi P là trung điểm của AB
Do tam giác OAB cân tại O nên OP ⊥ AB
Tam giác OAP vuông tại P có:
⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF
Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)
DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)
⇒ D; I; K thẳng hàng (1)
Ta có:
DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)
AI ⊥ BC ( AI là đường cao của tam giác ABC)
⇒ AI // BD
DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)
BI ⊥ BA ( BI là đường cao của tam giác ABC)
⇒ AD // BI
Xét tứ giác ADBI có: AI // BD và AD // BI
⇒ ADBI là hình bình hành
Do P là trung điểm của AB ⇒ P là trung điểm của DI
Hay D; P; I thẳng hàng (2)
Từ (1) và (2) ⇒ D; P; K thẳng hàng.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học ...
Môn: Toán 9
Thời gian làm bài: 45 phút
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 14
Bài 1: (1,5 điểm) Giải phương trình và hệ phương trình
a) 2x2 - 3x + 1 = 0
b) x3 - 3x2 + 2 = 0
Bài 2: (1,5 điểm)
a) Vẽ đồ thị (P) hàm số y = x2
b) Tìm m để đường thẳng (d) : y = 2x + m tiếp xúc với (P).
Bài 3: (1,5 điểm) Cho phương trình (ấn số x): x2 – 4x + m – 2 = 0 (1)
a) Giá trị nào của m thì phương trình (1) có nghiệm
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn 3x1 – x2 = 8
Bài 4: (1 điểm) Một ô tô đi từ A đến B với một vận tốc xác định. Nếu vận tốc tăng thêm 30 km/h thì thời gian đi sẽ giảm 1 giờ. Nếu vận tốc giảm bớt 15 km/h thì thời gian đi tăng thêm 1 giờ. Tính vận tốc và thời gian đi từ A đến B của ô tô.
Bài 5: (3,5 điểm) Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.
b) Chứng minh BE.BA = BI.BC
c) Chứng minh tứ giác OIED nội tiếp.
d) Cho biết BC = 16cm. Tính BE.BA + CD.CA
ĐÁP ÁN
Bài 1:
a) 2x2 - 3x + 1 = 0
a = 2; b = - 3; c = 1 ⇒ a + b + c = 0
Do đó phương trình có nghiệm x1 = 1; x2 = 1/2
b) x3 - 3x2 + 2 = 0
⇔ x3 - x2 - 2x2 + 2 = 0
⇔ x2(x - 1) - 2(x2 - 1) = 0
⇔ x2(x - 1) - 2(x + 1)(x - 1) = 0
⇔ (x - 1)[x2 - 2(x + 1)] = 0
⇔ (x - 1)(x2 - 2x - 2) = 0
* Ta có: x - 1 = 0 khi x = 1
* Xét x2 – 2x - 2 = 0 (*)
Có ∆' = (-1)2 - 1(-2) = 3 > 0 nên phương trình (*) có 2 nghiệm phân biệt:
x1 = 1 + √3; x2 = 1 - √3
Vậy phương trình đã cho có tập nghiệm là S = {1 - √3; 1; 1 + √3}
Khi đó hệ phương trình trở thành:
Bài 2:
a) Tập xác định của hàm số: R
Bảng giá trị
| x | - 2 | - 1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 2 |
Đồ thị hàm số y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.
b) Phương trình hoành độ giao điểm của (P) và (d) là x2 = 2x + m ⇔ x2 - 2x - m = 0
Δ' = 1-(-m) = 1 + m
(d) tiếp xúc với (P) khi và chỉ khi phương trình hoành độ giao điểm của (P) và d có một nghiệm duy nhất
⇔ Δ' = 0 ⇔ 1 + m = 0 ⇔ m = -1
Vậy với m = -1 thì d tiếp xúc với (P)
Bài 3:
a) Δ' = 22 - (m - 2) = 6 - m
Phương trình đã cho có nghiệm khi và chỉ khi Δ' ≥ 0
⇔ 6 - m ≥ 0 ⇔ m ≤ 6
Vậy với m ≤ 6 thì phương trình đã cho có nghiệm
b) Theo hệ thức Vi-et ta có:
Theo bài ra:
3x1 - x2 = 8
⇔ 3x1 - x2 = 2(x1 + x2)
⇔ x1 = 3x2
Khi đó: x1 + x2 = 4 ⇔ 3x2 + x2 = 4 ⇔ 4x2 = 4 ⇔ x2 = 1
⇒ x1 = 3
⇒ x1 x2 = 3 ⇒ m - 2 = 3 ⇔ m = 5
Vậy với m = 5 thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
Bài 4:
Gọi vận tốc dự định của ô tô là x (km/h) (x > 15)
Thời gian dự định đi của ô tô là y (h) (y > 1)
⇒ Quãng đường AB là xy (km)
Nếu vận tốc tăng 30 km/h thì thời gian giảm đi 1h nên ta có phương trình:
(x + 30)(y - 1) = xy ⇔ -x + 30y = 30 (1)
Nếu vận tốc giảm 15 km/h thì thời gian tăng 1h nên ta có phương trình
(x - 15)(y + 1) = xy ⇔ x - 15y = 15 (2)
Từ (1) và (2) ta có hệ phương trình:
Vậy vận tốc đi từ A đến B là 60 km/h
Thời gian đi từ A đến B là 3h.
Bài 5:
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90o (hai góc nội tiếp chắn nửa đườn tròn)
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = BC2 = 162 = 256
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 45 phút
Đề thi Học kì 2 Toán lớp 9 có đáp án đề số 15
Câu 1 (1,5 điểm): Giải các phương trình sau:
a)
b)
Câu 2 (1,5 điểm): Cho hàm số: có đồ thị là (P).
a) Vẽ (P).
b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D): bằng phép toán.
Câu 3 (1,5 điểm): Một khu vườn hình chữ nhật có chu vi 70m. Tính diện tích khu vườn biết 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m.
Câu 4 (1 điểm): Một xí nghiệp may cần thanh lý 1410 bộ quần áo. Biết mỗi ngày xí nghiệp đó bán được 30 bộ quần áo. Gọi x là số ngày đã bán, y là số bộ quần áo còn lại sau x ngày bán.
a) Hãy lập công thức tính y theo x.
b) Xí nghiệp cần bao nhiêu ngày để bán hết số bộ quần áo cần thanh lý?
Câu 5 (1 điểm):
Cho A là điểm thuộc nửa đường tròn (O) đường kính và . Tính AB, AC và diện tích phần tô đậm.
Câu 6 (1,5 điểm):
Cho phương trình: (x là ẩn).
a) Tìm m để phương trình có hai nghiệm và .
b) Gọi và là hai nghiệm của phương trình trên. Tìm m để .
Câu 7 (2 điểm):
Cho nhọn () nội tiếp đường tròn , các đường cao BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh .
c) DE, DF cắt đường tròn tại M và N. Chứng minh NM // EF.
Đáp án
Bài 1:
Phương pháp giải:
a) Sử dụng công thức nghiệm của phương trình bậc 2 để giải
b) Đặt để đưa phương trình đề bài thành phương trình bậc 2 sau đó dùng công thức nghiệm giải tìm t sau đó tìm x.
Lời giải chi tiết:
a)
Vậy phương trình có hai nghiệm phân biệt và
b)
Đặt khi đó phương trình trở thành: (1)
Giải phương trình (1), ta có:
Gọi là hai nghiệm phân biệt của (1)
Với ta có:
Vậy phương trình có hai nghiệm và
Bài 2:
Phương pháp giải:
a) Lập bảng giá trị và vẽ đồ thị.
b) Lập phương trình hoành độ giao điểm, giải phương trình bậc 2 để tìm.
Lời giải chi tiết:
Cho hàm số: có đồ thị là (P).
a) Vẽ (P).
Bảng giá trị:
|
x |
|
|
0 |
1 |
2 |
|
|
|
|
0 |
|
|
Vậy đồ thị hàm số là đường cong đi qua các điểm
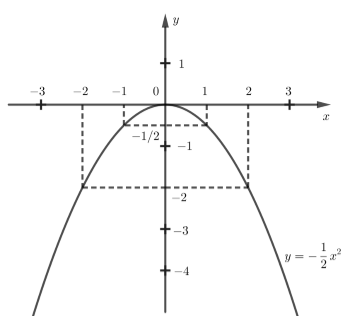
b) Tìm các tọa độ giao điểm của (P) và đường thẳng (D): bằng phép toán.
Phương trình hoành độ giao điểm của (P) và (D) là:
Ta có: hoặc
Với
Với
Vậy các giao điểm của (P) và (D) là 2 điểm và
Bài 3:
Phương pháp giải:
Phân tích đề bài, giải bài toán bằng cách lập hệ phương trình để tìm chiều dài chiều rộng khu vườn, sau đó tính diện tích.
Diện tích hình chữ nhật bằng tích của chiều dài với chiều rộng.
Lời giải chi tiết:
Gọi chiều dài và chiều rộng của khu vườn lần lượt là và
Vì khu vườn hình chữ nhật có chu vi 70m nên ta có:
Lại có 2 lần chiều dài nhỏ hơn 3 lần chiều rộng 5m nên ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
Vì khu vườn hình chữ nhật nên diện tích khu vườn là:
Vậy diện tích khu vườn là
Bài 4:
Phương pháp giải:
a) Tính số quần áo bán được sau x ngày bán từ đó suy ra y theo x.
b) Bán hết thì thế vào công thức ở a) để tính số ngày x.
Lời giải chi tiết:
a) Mỗi ngày xí nghiệp đó bán được 30 bộ quần áo nên sau x ngày bán xí nghiệp đó bán được 30x bộ quần áo.
y là số bộ quần áo còn lại sau x ngày bán (1)
b) Để xí nghiệp bán hết số bộ quần áo cần thanh lý thì
Thay vào (1) ta được:
(ngày)
Vậy xí nghiệp cần 47 ngày để bán hết số bộ quần áo cần thanh lý.
Bài 5:
Phương pháp giải:
Chứng minh tam giác ABC vuông tại A từ đó sử dụng mối quan hệ giữa cạnh và góc trong tam giác vuông để tính AB, AC.
Để tính diện tích phần tô đậm ta lấy diện tích nửa hình tròn (O) đường kính BC trừ đi diện tích tam giác ABC.
Lời giải chi tiết:
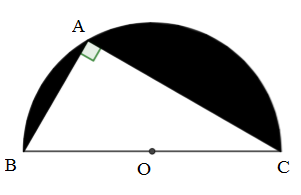
Ta có A là điểm thuộc nửa đường tròn (O) đường kính
(góc nội tiếp chắn nửa đường tròn)
Xét tam giác ABC vuông tại A ta có:
Gọi diện tích nửa hình tròn (O) đường kính là P
Gọi diện tích tam giác ABC là S
Gọi diện tích phần tô đậm là Q
Bài 6:
Phương pháp giải:
a) Sử dụng công thức nghiệm thu gọn, để phương trình có 2 nghiệm thì
b) Kết hợp câu a), biến đổi biểu thức đề bài sao cho chỉ còn và , sử dụng hệ thức Vi-ét thế vào để tìm m.
Lời giải chi tiết:
a) Tìm m để phương trình có hai nghiệm và .
Xét phương trình:
Có
Phương trình có hai nghiệm và
Vậy với thì phương trình có hai nghiệm và .
b) Gọi và là hai nghiệm của phương trình trên. Tìm m để .
Theo a) để phương trình có hai nghiệm và thì
Theo hệ thức Vi-ét ta có:
Ta có:
Vậy với thỏa mãn yêu cầu đề bài.
Bài 7:
Phương pháp giải:
a) Chứng minh A, E, H, F cùng thuộc một đường tròn để suy ra là tứ giác nội tiếp, chứng minh tứ giác BCEF có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc .
b) Chứng minh để suy ra đpcm
c) Chứng minh hai góc ở vị trí đồng vị bằng nhau dựa vào các định lý Talet thuận và đảo để suy ra các tam giác đồng dạng.
Lời giải chi tiết:
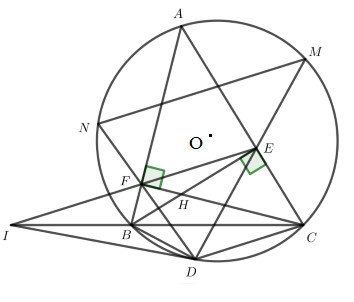
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Xét tứ giác có E, F thuộc đường tròn đường kính AH
A, E, H, F cùng thuộc một đường tròn đường kính
là tứ giác nội tiếp (dhnb).
Xét tứ giác có hay hai đỉnh kề nhau cùng nhìn cạnh dưới các góc vuông nên BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh .
Xét đường tròn có (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung )
Xét và có:
chung
(chứng minh trên)
c) DE, DF cắt đường tròn tại M và N. Chứng minh NM // EF.
Vì BCEF là tứ giác nội tiếp (theo câu a) nên xét đường tròn ngoại tiếp tứ giác có (hai góc nội tiếp cùng chắn cung )
Xét và có:
chung
(chứng minh trên)
Theo câu b) ta có
Xét và có:
chung
(2 góc tương ứng)
Mặt khác, xét đường tròn có ID là tiếp tuyến nên (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung )
Mà hai góc này ở vị trí đồng vị
Để xem trọn bộ Đề thi Toán 9 có đáp án, Thầy/ cô vui lòng Tải xuống!
Xem thêm các bộ đề thi lớp 9 chọn lọc, hay khác:
Đề thi Học kì 2 Sinh học lớp 9 năm 2022 - 2023 có đáp án
Đề thi Học kì 2 Ngữ văn lớp 9 năm 2022 - 2023 có đáp án
Đề thi Học kì 2 Địa Lí lớp 9 năm 2022 - 2023 có đáp án
Đề thi Học kì 2 Vật lí lớp 9 năm 2022 - 2023 có đáp án
Đề thi học kì 2 Lịch sử lớp 9 năm 2022 - 2023 có đáp án
Đề thi Học kì 2 Hoá học lớp 9 năm 2022 - 2023 có đáp án
Đề thi Học kì 2 Tiếng Anh lớp 9 năm 2022 - 2023 có đáp án
Xem thêm các chương trình khác:
- Góp ý sgk lớp 9 tất cả các môn năm 2024 - 2025 (3 bộ sách)
- Đề thi vào 10 môn Toán | Tuyển tập đề thi thử, đề chính thức vào lớp 10 môn Toán mới nhất
- Đề thi vào 10 môn Địa lí
- Đề thi vào 10 môn Văn | Tuyển tập đề thi thử, đề chính thức vào lớp 10 môn Ngữ Văn mới nhất
- Đề thi vào 10 môn Tiếng Anh | Tuyển tập đề thi thử, đề chính thức vào lớp 10 môn Tiếng Anh mới nhất