Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân
Với giải Bài 27 trang 67 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Luyện tập trang 67
Video giải Bài 27 trang 67 Toán lớp 7 Tập 2
Bài 27 trang 67 Toán lớp 7 Tập 2: Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Lời giải:
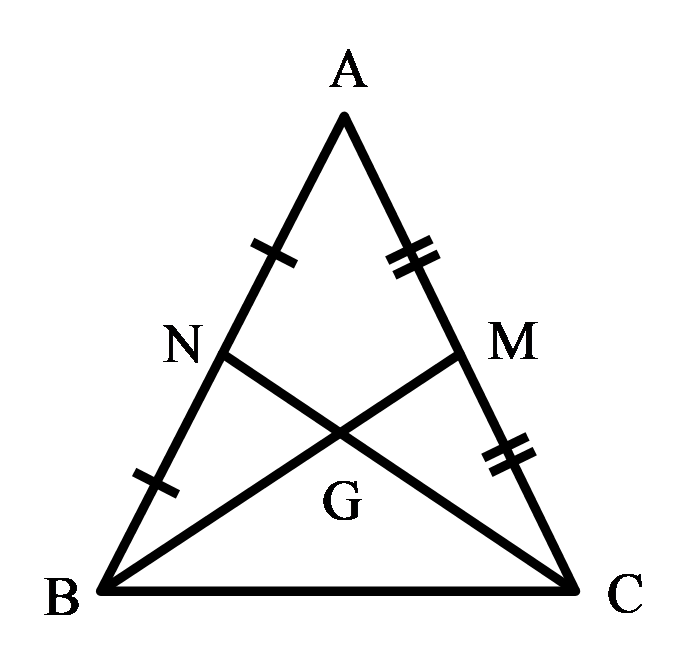
Giả sử ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G. Khi đó G là trọng tâm của tam giác ABC.
Mà BM = CN (theo giả thiết) nên suy ra GB = GC, GM = GN.
Xét ΔGNB và ΔGMC có :
GN = GM (chứng minh trên)
GB = GC (chứng minh trên)
(hai góc đối đỉnh)
Do đó ΔGNB = ΔGMC (c.g.c)
Suy ra NB = MC (hai cạnh tương ứng) (1)
Vì M, N là trung điểm của AC, AB nên ta có: AC = 2MC, AB = 2NB (2)
Từ (1) và (2) suy ra AB = AC.
Do đó ΔABC cân tại A.
Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:
Bài 28 trang 67 Toán 7 Tập 2: Cho tam giác DEF cân tại D với đường trung tuyến DI...
Bài 29 trang 67 Toán 7 Tập 2: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng...
Xem thêm các chương trình khác:
