Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm
Với giải Bài 30 trang 67 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Luyện tập trang 67
Video giải Bài 30 trang 67 Toán lớp 7 Tập 2
Bài 30 trang 67 Toán lớp 7 Tập 2: Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC.
Lời giải:
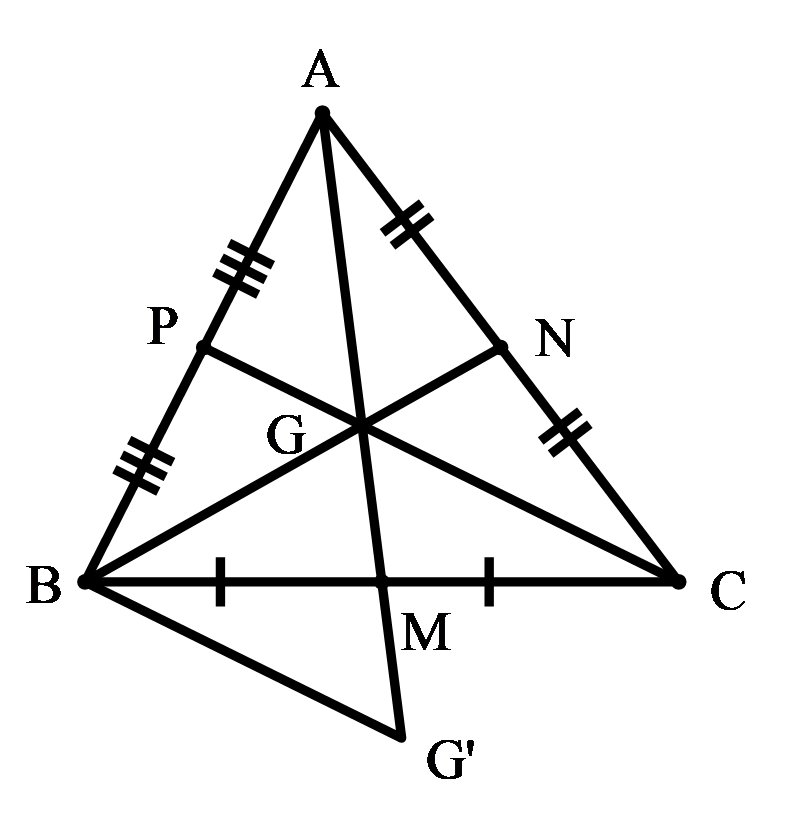
a) Gọi trung điểm BC, AC, AB lần lượt là M, N, P.
⇒ AM, BN, CP là các đường trung tuyến, G là trọng tâm của ΔABC.
Theo tính chất đường trung tuyến của tam giác ta có:
(1)
mà GA = GG’ (do G là trung điểm của AG’) nên (2)
, mà
Xét ΔGMC và ΔG’MB có:
GM = G’M (chứng minh trên)
(hai góc đối đỉnh)
MC = MB (giả thiết)
Do đó ΔGMC = ΔG’MB (c.g.c).
Suy ra GC = G’B (hai cạnh tương ứng).
Mà (tính chất đường trung tuyến) (3)
Từ (1), (2), (3) ta có:
b) Gọi I, K lần lượt là trung điểm của BG, BG’.
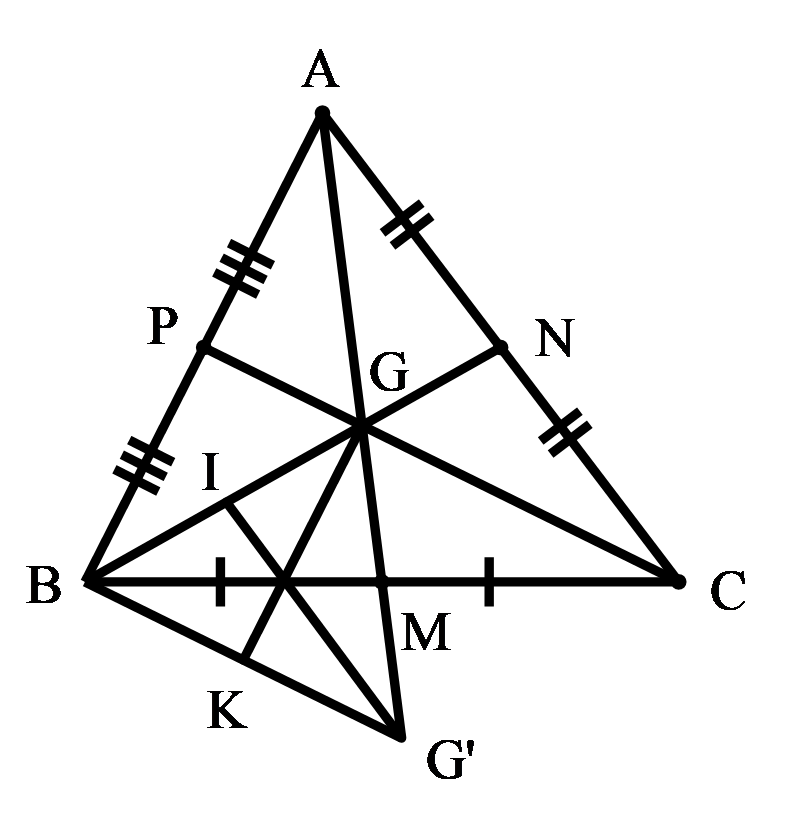
Vì M là trung điểm GG’nên BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC nên
Vì I là trung điểm của BG nên .
Mà nên suy ra .
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
(hai góc đối đỉnh).
GG’ = GA (giả thiết)
Do đó ΔIGG’ = ΔNGA (c.g.c)
Suy ra G’I = AN (hai cạnh tương ứng)
(vì )
Ta có:
Mà GC = BG’ (chứng minh phần a) nên suy ra PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)
(hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên suy ra CP // BG’.
(hai góc so le trong) hay .
Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
(chứng minh trên)
BG là cạnh chung
Do đó ΔPGB = ΔKBG (c.g.c)
Suy ra PB = GK (hai cạnh tương ứng)
(vì ).
Vậy
Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:
Bài 28 trang 67 Toán 7 Tập 2: Cho tam giác DEF cân tại D với đường trung tuyến DI...
Bài 29 trang 67 Toán 7 Tập 2: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng...
Xem thêm các chương trình khác:
