Trắc nghiệm Toán 7 Bài 3. Hai đường thẳng song song có đáp án
Trắc nghiệm Toán 7 Bài 3. Hai đường thẳng song song có đáp án
-
572 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
12/11/2024Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải;
Theo tiên đề Euclid ta có: qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Phương pháp giải
Sử dụng lý thuyết về tiên đề Euclid
*Lý thuyết:
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
2. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau.
b) Hai góc đồng vị bằng nhau.
c) Hai góc trong cùng phía bù nhau.
Xem thêm
Lý thuyết Tiên đề Euclid. Tính chất của hai đường thẳng song song – Toán 7 Kết nối tri thức
Câu 2:
18/07/2024Nếu một đường thẳng cắt hai đường thẳng song song thì:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc đồng vị bằng nhau;
Hai góc so le trong bằng nhau.
Câu 3:
20/12/2024Cho hình vẽ dưới đây:
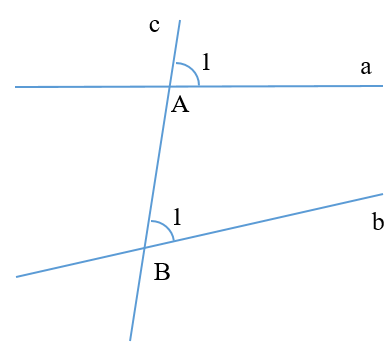
^A1 và ^B1 là hai góc:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
^A1 và ^B1 là hai góc đồng vị.
*Phương pháp giải;
Áp dụng lý thuyết 2 góc đồng vị
*Lý thuyết;
Các góc tạo bởi một đường thẳng cắt hai đường thẳng
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:
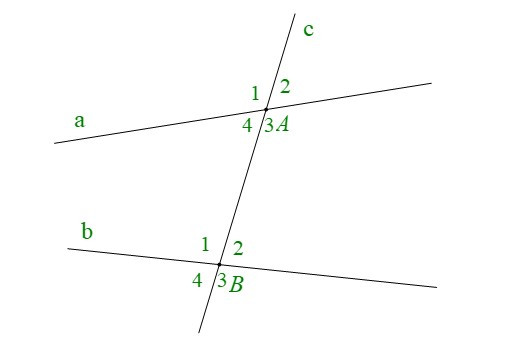
+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Xem thêm
Lý thuyết Hai đường thẳng song song và dấu hiệu nhận biết – Toán 7 Kết nối tri thức
TOP 15 câu Trắc nghiệm Toán lớp 7 (Chân trời sáng tạo 2024) có đáp án: Hai đường thẳng song song
Câu 4:
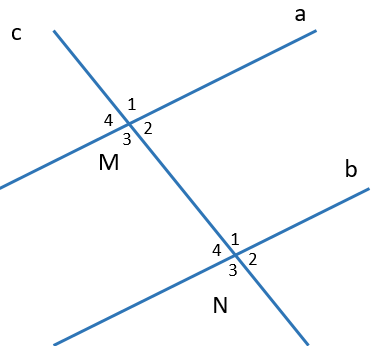
20/07/2024Chọn phát biểu đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
^M1 và ^N1 là hai góc so le trong là phát biểu sai, vì đó là hai góc đồng vị, loại phương án A;
^M2 và ^N2 là hai góc so le ngoài là phát biểu sai, vì đó là hai góc đồng vị, loại phương án B;
^M3 và ^N1 là hai góc đồng vị là phát biểu sai, vì đó là hai góc so le trong, loại phương án C;
^M4 và ^N4 là hai góc đồng vị là phát biểu đúng, chọn phương án D.
Câu 5:
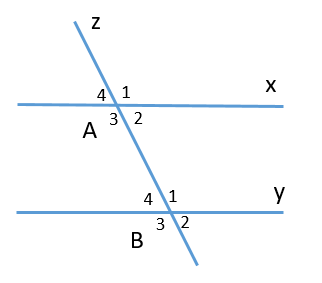
18/07/2024Chọn một cặp góc đồng vị trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
^B2 và ^B3 là hai góc đồng vị là phát biểu sai, vì ^B2 và ^B3 là hai góc kề bù, loại phương án A.
^B2 và ^B3 là hai góc đồng vị là phát biểu đúng, chọn phương án B.
^A2 và ^B4 là hai góc đồng vị là phát biểu sai, vì ^A2 và ^B4 là hai góc so le trong, loại phương án C.
^A4 và ^A2 là hai góc đồng vị là phát biểu sai, vì ^A4 và ^A2 là hai góc đối đỉnh, loại phương án D.
Câu 6:
18/07/2024Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì x, y song song với nhau.
Câu 7:
23/07/2024Cho hình vẽ
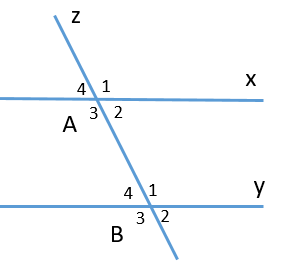
Biết một cặp góc đồng vị ^A4=^B4=30∘. Tính số đo của cặp góc đồng vị ^A3 và ^B3.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D

Ta có:
^A4+^B3=180∘ (hai góc kề bù)
⇒^B3=180∘−30∘=150∘
⇒^A3=^B3=150∘
=> Chọn phương án D.
Câu 8:
22/07/2024Biết một cặp góc so le trong ^A2=^B4=36∘. Tính số đo của cặp góc so le trong còn lại:

 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
^A2+^A3=180∘ (hai góc kề bù)
⇒^A3=180∘−36o=144∘
Mà ^A2 và ^B4; ^A3 và ^B1 là hai cặp góc so le trong.
Do đó, ^A3=^B1=144∘
Vậy số đo của cặp góc so le trong còn lại là ^A3=^B1=144∘.
Câu 9:
22/07/2024Cho hình vẽ
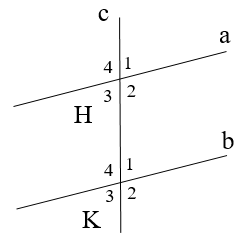
Biết ^K1=^H3=42∘.. Tính ^H3+^K4
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét hai đường thẳng a và b cùng cắt đường thẳng c có: ^K1=^H3
Mà hai góc này ở vị trí so le trong nên a // b
Suy ra ^H3+^K4=180∘ (hai góc ở vị trí trong cùng phía)
Vậy ^H3+^K4=180∘
Câu 10:
20/07/2024Cho hình vẽ

Biết a // b, ^H3=42∘. Tính số đo ^K3
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì a // b nên ^H3=^K3 ( do ^H3 và ^K3 là hai góc đồng vị).
Suy ra ^K3=42∘.
Vậy ^K3=42∘.
Câu 11:
18/07/2024Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
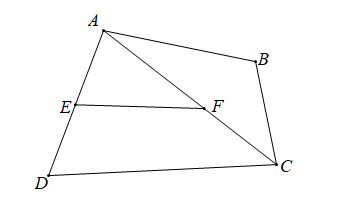
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
^DAC và ^AFE là hai góc so le trong là phát biểu sai, vì ^DAC và ^AFE là hai góc trong một tam giác loại phương án A.
^AFE và ^BAC là hai góc so le trong là phát biểu đúng, chọn phương án B.
^AFE và ^ADC là hai góc đồng vị là phát biểu sai.
^BAC và ^DAC là hai góc đồng vị là phát biểu sai, vì ^BAC và ^DAC có đỉnh chung và có một cạnh chung nên là hai góc kề nhau, do đó loại phương án D.
Câu 12:
20/12/2024Cho hình vẽ
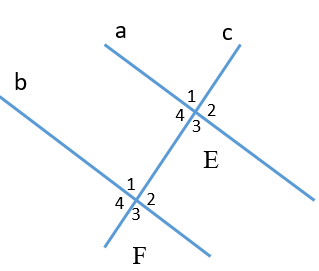
Biết a // b,
ˆE1=51∘. Số đo ^F3 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Lời giải
Ta có: ^E1 và ^F1 là hai góc đồng vị và a // b => ^E1=^F1=51∘
Mà ta lại có ^F1 và ^F3 là hai góc đối đỉnh nên => ^F1=^F3
⇒^F3=51∘
Vậy ^F3=51∘.
*Phương pháp giải;
Áp dụng lý thuyết 2 góc đồng vị, 2 góc đối đỉnh
*Lý thuyết;
Các góc tạo bởi một đường thẳng cắt hai đường thẳng
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:

+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Khi hai đường thẳng a và b cắt nhau, chúng tạo thành các cặp góc đối đỉnh như minh họa trong hình vẽ.
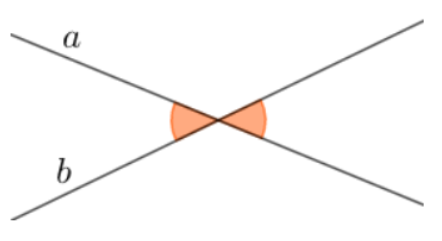
Còn có một cặp góc đối đỉnh khác:
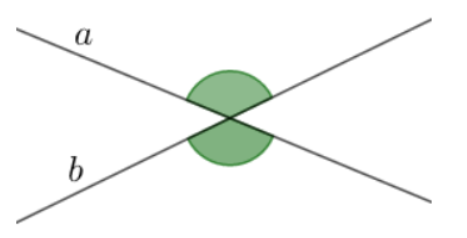
Khi hai đường thẳng cắt nhau, chúng tạo ra hai cặp góc đối đỉnh.
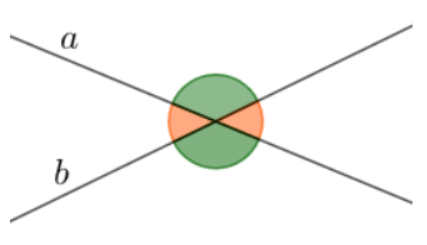
2. Tính chất của hai góc đối đỉnh
- Hai góc đối đỉnh luôn bằng nhau
Xem thêm
Lý thuyết Hai đường thẳng song song và dấu hiệu nhận biết – Toán 7 Kết nối tri thức
TOP 15 câu Trắc nghiệm Toán lớp 7 (Chân trời sáng tạo 2024) có đáp án: Hai đường thẳng song song
Câu 13:
18/07/2024Trong các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau
(II) Hai góc so le trong bằng nhau
(III) Hai góc bù nhau bằng nhau
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
Hai góc bù nhau là hai góc có tổng số đo bằng 180o
=> Có 2 câu đúng, chọn đáp án C.
Câu 14:
20/07/2024Cho hai điểm phân biệt M, N. Ta vẽ một đường thẳng a đi qua điểm M và một đường thẳng b đi qua điểm N sao cho a // b. Có thể vẽ được bao nhiêu cặp đường thẳng a, b thỏa mãn điều kiện trên.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
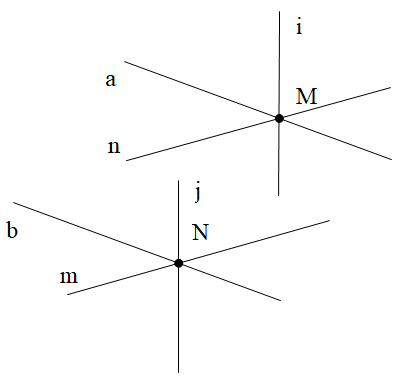
Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Cứ tương ứng với mỗi một đường thẳng đi qua M thì ta vẽ được một đường thẳng đi qua N (theo Tiên đề Euclid) và song song với đường thẳng đó. Trên hình vẽ ta có b //a, m // n, j // i.
Vậy ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Câu 15:
18/07/2024Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
Do đó, qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì hai đường thẳng đó phải trùng nhau.
=> Chọn đáp án A.
Có thể bạn quan tâm
Các bài thi hot trong chương
- Trắc nghiệm Toán 7 Bài 1. Góc ở vị trí đặc biệt có đáp án (4282 lượt thi)
- Trắc nghiệm Toán 7 Bài 2. Tia phân giác của một góc có đáp án (573 lượt thi)
- Trắc nghiệm Toán 7 Bài 4. Định lí có đáp án (559 lượt thi)
- Trắc nghiệm Toán 7 Bài tập cuối chương 4 có đáp án (433 lượt thi)
