Trắc nghiệm Toán 7 Bài 4. Định lí có đáp án
-
479 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Định lí thường được phát biểu dưới dạng:
Xem đáp án
Đáp án đúng là: B
Định lí thường được phát biểu dưới dạng “Nếu … thì …”.
|
Giả thiết |
\[a \bot c,\;b \bot c\] |
|
Kết luận |
a // b |
Câu 2:
23/07/2024Phát biểu định lý sau thành lời:
Xem đáp án
Đáp án đúng là: A
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Câu 3:
22/07/2024Định lí: “Nếu hai đường thẳng song song cùng cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau”. Giả thiết của định lí là:
Xem đáp án
Đáp án đúng là: A.
Giả thiết của định lí trên là \[a//b;\;c\, \cap \,a = \left\{ M \right\};\;c\, \cap b = \left\{ N \right\}\].
Câu 4:
18/07/2024Chọn phát biểu đúng
Xem đáp án
Đáp án đúng là: C
Giả thiết của định lí là phần cho biết. Kết luận của định lí là điều suy ra.
Câu 5:
19/07/2024Điền vào chỗ trống những nội dung thích hợp để được định lí đúng.
Nếu … thì \[NA = NB = \frac{1}{2}AB\].
Xem đáp án
Đáp án đúng là: B
Nếu N là trung điểm của AB thì \[NA = NB = \frac{1}{2}AB\].
Câu 6:
19/07/2024Điền vào chỗ trống nội dung thích hợp.
“Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng ….”
Xem đáp án
Đáp án đúng là: A
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một góc đồng vị bằng nhau thì a, b song song với nhau.
Câu 7:
22/07/2024Điền vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng song song thì …”
Xem đáp án
Đáp án đúng là: D
Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc đồng vị bằng nhau;
+ Hai góc so le trong bằng nhau.
Câu 8:
23/07/2024Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Hình vẽ minh hoạ cho định lí trên là:
Xem đáp án
Đáp án đúng là: A
Hình vẽ ở phương án B không thoả mãn điều kiện hai đường thẳng a và b song song với nhau.
Hình vẽ ở phương án C và D không thoả mãn điều kiện đường thẳng c vuông góc với một trong hai đường thẳng a và b song song với nhau.
Câu 9:
18/07/2024Viết giả thiết cho định lí sau:
“Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
Xem đáp án
Đáp án đúng là: A
Giả thiết của định lí “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau” là: \[a \ne b;\;a\,//c,\;b\,//c\].
Câu 10:
23/07/2024Điền vào chỗ trống.
Nếu hai góc đối đỉnh thì ….
Xem đáp án
Đáp án đúng là: C
Nếu hai góc đối đỉnh thì hai góc đó bằng nhau.
Câu 11:
18/07/2024Trong định lí, phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết vậy phần nằm sau từ “thì” là phần?
Xem đáp án
Đáp án đúng là: A
Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết vậy phần nằm sau từ “thì” là phần kết luận.
Câu 12:
22/07/2024Phát biểu định lí sau bằng lời.
|
Giả thiết |
c cắt a tại M, c cắt b tại N \[\widehat {{N_1}}\] và \[\widehat {{M_1}}\]là hai góc đồng vị \[\widehat {{N_1}} = \widehat {{M_1}}\] |
|
Kết luận |
a // b |
Xem đáp án
Đáp án đúng là: B
Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng a, b song song với nhau.
Câu 13:
20/07/2024Vẽ hình minh họa nội dung định lí sau:
“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”
Xem đáp án
Đáp án đúng là: A
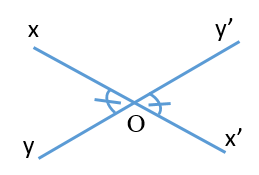
Câu 14:
19/07/2024Viết giả thiết, kết luận cho định lí sau:
“Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”
Xem đáp án
Đáp án đúng là: A
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} = \widehat {{B_1}}\] |
|
Kết luận |
a // b |
Câu 15:
19/07/2024Chứng minh định lí là:
Xem đáp án
Đáp án đúng là: A
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.