Trắc nghiệm Toán 10 CTST Bài tập cuối chương 3 có đáp án (Nhận biết)
-
460 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho bảng dữ liệu sau đây cho biết số lượng các mặt hàng bán được trong 4 tuần vừa qua của một cửa hàng văn phòng phẩm:
|
Mặt hàng |
Vở trắng |
Bút bi |
Tẩy |
Bút chì |
Thước |
|
Số lượng |
200 |
350 |
150 |
380 |
270 |
Bảng dữ liệu trên có biểu thị một hàm số không? Nếu có hãy xác định tập xác định và tập giá trị của hàm số đó.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Từ bảng dữ liệu đã cho, ta thấy ứng với mỗi mặt hàng trong bảng đều có một giá trị số lượng bán được duy nhất.
Vì vậy bảng trên biểu thị một hàm số.
Hàm số đó có:
+) Tập xác định D = {Vở trắng; Bút bi; Tẩy; Bút chì; Thước}.
+) Tập giá trị T = {200; 350; 150; 380; 270}.
Vậy ta chọn phương án B.
Câu 2:
18/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = –4, c = 3.
Vì b = –4 nên ta có b’ = –2.
∆’ = b’2 – ac = (–2)2 – (–1).3 = 7.
Đỉnh S có tọa độ:
⦁ \({x_S} = - \frac{{b'}}{a} = - \frac{{ - 2}}{{ - 1}} = - 2\);
⦁ \({y_S} = - \frac{{\Delta '}}{a} = - \frac{7}{{ - 1}} = 7\).
Suy ra tọa độ đỉnh S(–2; 7).
Vậy ta chọn phương án C.
Câu 3:
14/07/2024Biểu đồ sau đây cho biết tốc độ tăng GDP các năm của Việt Nam giai đoạn 2016 – 2020 (Nguồn: Báo Lao động):
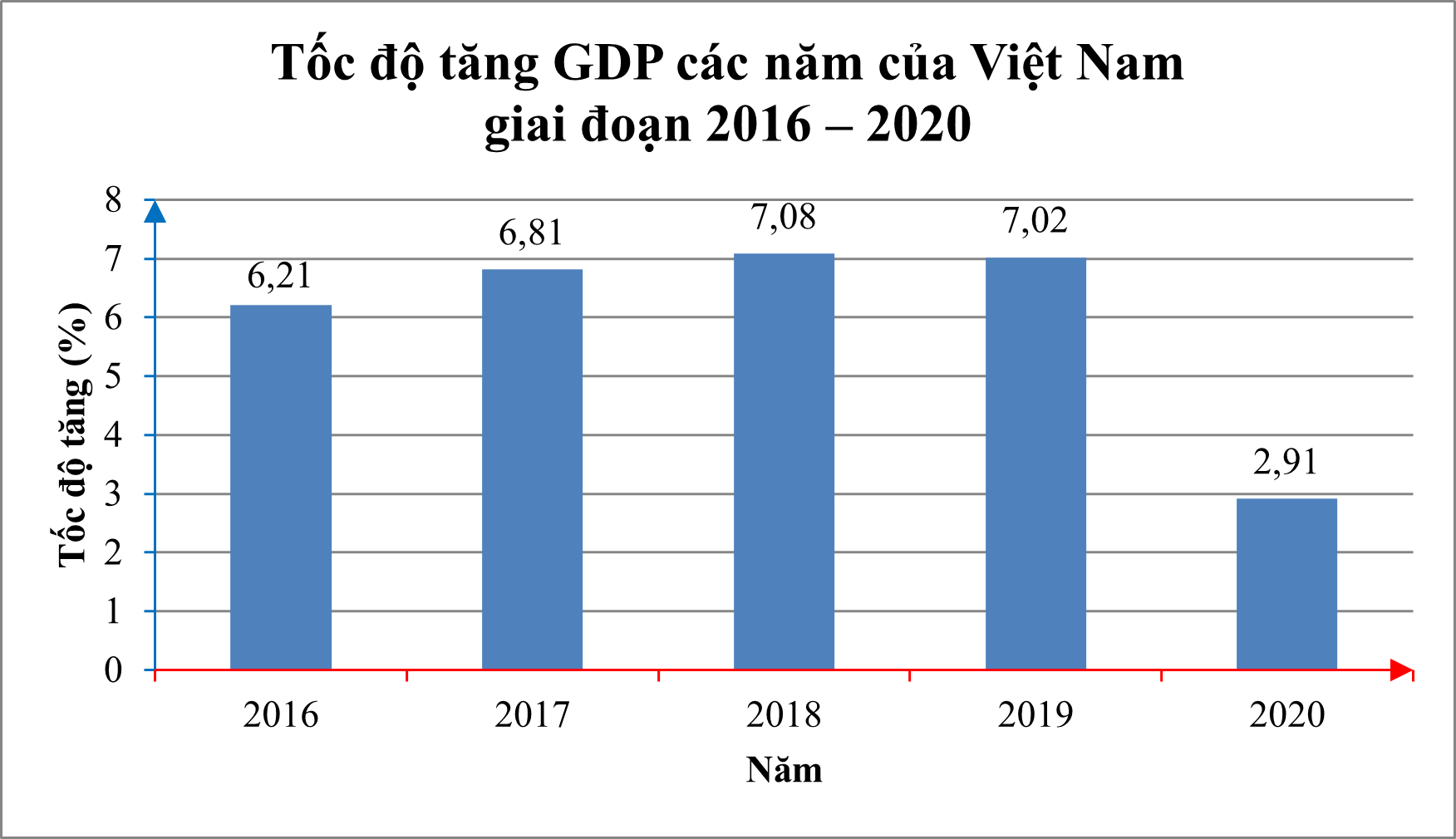
Biểu đồ trên có biểu thị cho ta một hàm số không? Nếu có hãy xác định tập xác định và tập giá trị của hàm số đó.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Từ biểu đồ đã cho, ta thấy ứng với mỗi thời điểm (năm) trong biểu đồ đều có một giá trị tốc độ tăng duy nhất.
Vì vậy biểu đồ trên biểu thị một hàm số.
Hàm số đó có:
+) Tập xác định D = {2016; 2017; 2018; 2019; 2020};
+) Tập giá trị T = {6,21; 6,81; 7,08; 7,02; 2,91}.
Vậy ta chọn phương án A.
Câu 4:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số đã cho có dạng y = ax2 + bx + c, với a = 1, b = 2, c = –3.
Trục đối xứng của hàm số đã cho là đường thẳng \(x = - \frac{b}{{2a}} = - \frac{2}{{2.1}} = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy).
Vậy ta chọn phương án C.
Câu 5:
19/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Khi hàm số đồng biến (tăng) trên tập xác định của nó thì đồ thị của hàm số đó có dạng đi lên từ trái sang phải hay có dạng đi xuống từ phải sang trái.
Vậy ta chọn phương án B.
Câu 6:
22/11/2024 Xem đáp án
Đáp án đúng là: D
Lời giải
Hàm số bậc hai có dạng y = ax2 + bx + c (với a ≠ 0).
Ta thấy hàm số ở đáp án D có dạng như trên nên hàm số ở đáp án D là hàm số bậc hai.
Vậy ta chọn đáp án D.
*Phương pháp giải:
Hàm số bậc hai có dạng y = ax2 + bx + c, với a ≠ 0.
*Lý thuyết:
1. Khái niệm hàm số bậc hai
Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + c, trong đó x là biến số, a, b, c là các hằng số và a ≠ 0.
Tập xác định của hàm số bậc hai là ℝ.
Nhận xét : Hàm số y = ax2 (a ≠ 0) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.
Ví dụ:
a) Hàm số y = 2x2 + x – 1 là hàm số bậc hai với a = 2, b = 1, c = –1.
b) Hàm số y = – x2 cũng là hàm số bậc hai với a = –1 và b = c = 0.
2. Đồ thị của hàm số bậc hai
- Đồ thị của hàm số bậc hai là một parabol.
- Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm , có trục đối xứng là đường thẳng . Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
- Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau :
1. Xác định tọa độ đỉnh ;
2. Vẽ trục đối xứng ;
3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol ;
4. Vẽ parabol.
Nhận xét : Từ đồ thị hàm số y = ax2 + bx + c (a ≠ 0), ta suy ra tính chất của hàm số y = ax2 + bx + c (a ≠ 0):
|
Với a > 0 |
Với a < 0 |
|
Hàm số nghịch biến trên khoảng ; Hàm số đồng biến trên khoảng ; là giá trị nhỏ nhất của hàm số. |
Hàm số đồng biến trên khoảng ; Hàm số nghịch biến trên khoảng ; là giá trị lớn nhất của hàm số. |
Xem thêm
Lý thuyết Hàm số bậc hai - Toán 10 Kết nối tri thức
Câu 7:
22/07/2024 Xem đáp án
Đáp án đúng là: D
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 5, c = –4.
∆ = b2 – 4ac = 52 – 4.(–1).(–4) = 9.
Vì a = –1 < 0 nên hàm số đạt giá trị lớn nhất bằng \(\frac{{ - \Delta }}{{4a}} = \frac{{ - 9}}{{4.\left( { - 1} \right)}} = \frac{9}{4}\) tại \(x = \frac{{ - b}}{{2a}} = \frac{{ - 5}}{{2.\left( { - 1} \right)}} = \frac{5}{2}\).
Vậy hàm số đạt giá trị lớn nhất bằng \(\frac{9}{4}\) tại \(x = \frac{5}{2}\).
Ta chọn phương án D.
Câu 8:
19/07/2024Cho hàm số y = f(x) = x2 + 3x + 4. Bảng giá trị của hàm số đã cho là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét hàm số y = f(x) = x2 + 3x + 4.
• Với x = –3, ta có f(–3) = (–3)2 + 3.(–3) + 4 = 4.
• Với x = –2, ta có f(–2) = (–2)2 + 3.(–2) + 4 = 2.
• Với x = \[ - \frac{3}{2}\], ta có \(f\left( { - \frac{3}{2}} \right) = {\left( { - \frac{3}{2}} \right)^2} + 3.\left( { - \frac{3}{2}} \right) + 4 = \frac{7}{4}\).
• Với x = –1, ta có f(–1) = (–1)2 + 3.(–1) + 4 = 2.
• Với x = 0, ta có f(0) = 02 + 3.0 + 4 = 4.
Vậy bảng giá trị của hàm số đã cho là:
|
x |
–3 |
–2 |
\[ - \frac{3}{2}\] |
–1 |
0 |
|
f(x) |
4 |
2 |
\(\frac{7}{4}\) |
2 |
4 |
Do đó ta chọn đáp án C.
Câu 9:
19/07/2024Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ:
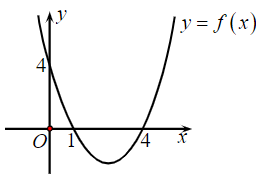
Đặt ∆ = b2 – 4ac. Tìm dấu của a và ∆.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.
Lại có đồ thị cắt trục Ox tại hai điểm phân biệt (cụ thể là tại x = 1 và x = 4) nên phương trình ax2 + bx + c = 0 có hai nghiệm x1, x2.
Do đó ∆ > 0.
Vậy a > 0, ∆ > 0.
Do đó ta chọn phương án A.
Câu 10:
12/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta đặt \(y = f\left( x \right) = - \frac{x}{2} + 2\).
• Với x = 0, ta có f(0) = \( - \frac{0}{2} + 2 = 2\).
Khi đó đồ thị hàm số đã cho đi qua điểm M(0; 2).
Do đó ta loại phương án C và D.
• Với y = 0, ta có f(x) = \( - \frac{x}{2} + 2 = 0\)
Þ \( - \frac{x}{2} = - 2\) Þ x = 4.
Khi đó đồ thị hàm số đã cho đi qua điểm N(4; 0).
Do đó ta loại phương án B.
Vì vậy đồ thị ở phương án A là đồ thị của hàm số đã cho.
Vậy ta chọn phương án A.