Trắc nghiệm Toán 10 CTST Bài 2. Định lý côsin và định lý sin có đáp án
Dạng 1: Xác định các cạnh và góc chưa biết trong tam giác có đáp án
-
738 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Theo định lý côsin, ta có:
BC2 = AB2 + AC2 −2.AB.AC.cosA = 72 + 102 −2.7.10.cos112° ≈ 201,44.
Vậy \(BC \approx \sqrt {201,44} \approx 14,19\).
Theo hệ quả của định lý cô sin, ta có:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} \approx \frac{{{{10}^2} + {{14,19}^2} - {7^2}}}{{2.10.14,19}} \approx 0,89\).
Suy ra \[\widehat B \approx 27^\circ 7'\].
Ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right)\)
Do đó: \(\widehat C \approx 40^\circ 53'\).
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đặt a = BC, b = AC, c = AB.
Ta có a = 15.
Áp dụng định lí tổng 3 góc trong tam giác ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right)\)\( = 180^\circ - \left( {63^\circ + 87^\circ } \right) = 30^\circ \).
Áp dụng định lý sin, ta có \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\).
Suy ra \(AC = b = \frac{{a\sin B}}{{\sin A}} = \frac{{15.\sin 87^\circ }}{{\sin 63^\circ }} \approx 16,81\);
\(AB = c = \frac{{a\sin C}}{{\sin A}} = \frac{{15.\sin 30^\circ }}{{\sin 63^\circ }} \approx 8,42\).
Câu 3:
11/07/2024Cho tam giác ABC có a = 4, b = 6 và cosC = \(\frac{2}{3}\). Giá trị của c bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Áp dụng định lý côsin vào tam giác ABC ta có:\({c^2} = {a^2} + {b^2} - 2ab\cos C\)
Thay số
\({c^2} = {4^2} + {6^2} - 2.4.6.\frac{2}{3} = 20\).
Do đó: \(c = \sqrt {20} = 2\sqrt 5 \).
Câu 4:
12/07/2024Cho tam giác DEF có DE = 4 cm; DF = 5 cm và EF = 3 cm. Số đo của của góc D gần nhất với giá trị nào dưới đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Áp dụng hệ quả của định lý côsin vào tam giác DEF ta được:
\(\cos D = \frac{{D{E^2} + D{F^2} - E{F^2}}}{{2.DE.DF}} = \frac{{{4^2} + {5^2} - {3^2}}}{{2.4.5}} = \frac{4}{5}\).
Do đó \(\widehat D \approx 36,87^\circ \).
Câu 5:
19/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Theo định lí sin ta có
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)\( \Rightarrow a = \frac{{b.\sin A}}{{\sin B}}\)\( = \frac{{4.\sin 60^\circ }}{{\sin 45^\circ }} = 2\sqrt 6 \).
Câu 6:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Áp dụng định lý sin ta có:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} \Rightarrow \sin P = \frac{{MN.\sin N}}{{MP}} = \frac{{5.\sin 60^\circ }}{8} = \frac{{5\sqrt 3 }}{{16}}\)
\( \Rightarrow \widehat P \approx 32^\circ 46'\) (do góc P nhọn)
\( \Rightarrow \widehat M \approx 180^\circ - 60^\circ - 32^\circ 46' = 87^\circ 14'\) (suy ra từ định lí tổng 3 góc trong tam giác).
Câu 7:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Áp dụng định lý côsin trong tam giác ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos B\)
Thay số: \(A{C^2} = {4^2} + {6^2} - 2.4.6.\cos 120^\circ = 76\)
\( \Rightarrow AC = 2\sqrt {19} \).
Vậy độ dài của cạnh AC là \(2\sqrt {19} \).
Câu 8:
19/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Xét tam giác ABC có: 7 > 6 > 5, suy ra: AB > CA > BC
\( \Rightarrow \widehat C > \widehat B > \widehat A\)( quan hệ giữa góc và cạnh đối diện: trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).
Vậy góc có số đo lớn nhất trong tam giác là góc C.
Áp dụng định lý côsin trong tam giác ABC ta có:
\(\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}} = \frac{{{6^2} + {5^2} - {7^2}}}{{2.6.5}} = \frac{1}{5}\).
Câu 9:
16/07/2024Cho tam giác ABC có \(\widehat A = 120^\circ \), AB = 1, AC = 2. Trên tia CA kéo dài lấy điểm D sao cho BD = 2. Tính AD.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
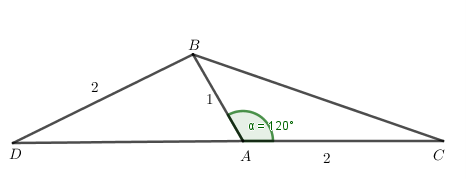
Ta có: \(\widehat {BAD} + \widehat {BAC} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {BAD} = 180^\circ - \widehat {BAC} = 180^\circ - 120^\circ = 60^\circ \) nên cos\(\widehat {BAD} = \frac{1}{2}\).
Do đó áp dụng định lí côsin trong tam giác ABD, ta có:
\(\cos \widehat {BAD} = \frac{{A{D^2} + A{B^2} - B{D^2}}}{{2.AD.AB}}\)\( \Leftrightarrow \frac{1}{2} = \frac{{A{D^2} + {1^2} - {2^2}}}{{2.AD.1}}\)
\[ \Leftrightarrow A{D^2} - AD - 3 = 0\]
\( \Rightarrow AD = \frac{{1 + \sqrt {13} }}{2}\) (do AD > 0).
Câu 10:
22/07/2024Cho góc xOy bằng 60°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = \(4\sqrt 3 \). Tính độ dài đoạn OA để OB có độ dài lớn nhất.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
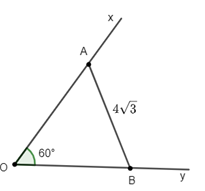
Áp dụng định lý sin trong tam giác OAB ta có:
\(\frac{{OB}}{{\sin \widehat {OAB}}} = \frac{{AB}}{{\sin \widehat {AOB}}}\)
\( \Rightarrow OB = \frac{{AB.\sin \widehat {OAB}}}{{\sin \widehat {AOB}}} = \frac{{4\sqrt 3 .\sin \widehat {OAB}}}{{\sin 60^\circ }} = 8.\sin \widehat {OAB}\).
Mà \(\sin \widehat {OAB} \le 1 \Rightarrow OB \le 8\).
Suy ra maxOB = 8 \( \Leftrightarrow \sin \widehat {OAB} = 1 \Rightarrow \widehat {OAB} = 90^\circ \)
Suy ra tam giác OAB vuông tại A.
Do đó \(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{8^2} - {{\left( {4\sqrt 3 } \right)}^2}} = 4\).
Câu 11:
18/07/2024Cho tam giác ABC nhọn biết a = \(\sqrt {24} \), c = \(2 + \sqrt {12} \) và bán kính của đường tròn ngoại tiếp tam giác ABC là R = \(2\sqrt 2 \). Tìm cạnh b của tam giác ABC biết b là số nguyên.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Áp dụng định lý sin trong tam giác ABC có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
\( \Leftrightarrow \frac{{\sqrt {24} }}{{\sin A}} = \frac{b}{{\sin B}} = \frac{{2 + \sqrt {12} }}{{\sin C}} = 4\sqrt 2 \)
Do đó \(\left\{ {\begin{array}{*{20}{c}}{\sin A = \frac{{\sqrt {24} }}{{4\sqrt 2 }} = \frac{{\sqrt 3 }}{2}}\\{\sin C = \frac{{2 + \sqrt {12} }}{{4\sqrt 2 }} = \frac{{\sqrt 6 + \sqrt 2 }}{4}}\end{array}} \right.\), suy ra \(\left\{ {\begin{array}{*{20}{c}}{\widehat A = 60^\circ }\\{\widehat C = 75^\circ }\end{array}} \right.\) (do tam giác ABC nhọn).
Trong tam giác ABC có \(\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) = 180^\circ - \left( {60^\circ + 75^\circ } \right) = 45^\circ \).
Từ đó ta có: \(\frac{b}{{\sin 45^\circ }} = 4\sqrt 2 \Rightarrow b = \sin 45^\circ .4\sqrt 2 = 4\).
Câu 12:
12/07/2024Cho tam giác ABC biết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) và \(AB = 2\sqrt 2 \). Tính AC.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Áp dụng định lý sin trong tam giác ABC, ta có
\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Leftrightarrow \frac{{\sin B}}{{\sin C}} = \frac{b}{c} = \frac{{AC}}{{AB}}\)
Từ \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) suy ra \(\frac{{AC}}{{AB}} = \sqrt 3 \Leftrightarrow AC = AB\sqrt 3 = 2\sqrt 2 .\sqrt 3 = 2\sqrt 6 \).
Bài thi liên quan
-
Dạng 2: Chứng minh các đẳng thức, hệ thức liên quan có đáp án
-
12 câu hỏi
-
30 phút
-
-
Dạng 3: Cách tính bán kính đường tròn nội tiếp, ngoại tiếp của tam giác có đáp án
-
12 câu hỏi
-
30 phút
-
-
Dạng 4: Các cách tính diện tích tam giác có đáp án
-
12 câu hỏi
-
30 phút
-
-
Dạng 5: Chứng minh dạng tam giác (vuông, nhọn, tù) có đáp án
-
14 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án (856 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2. Định lý côsin và định lý sin có đáp án (737 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án (352 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 CTST Bài 2. Hàm số bậc hai có đáp án (1352 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1: Mệnh đề có đáp án (955 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án (901 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án (832 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1: Xác định vectơ. Tìm điểm đầu, điểm cuối, giá của vectơ có đáp án (785 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án (728 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2: Tập hợp có đáp án (666 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1: Bất phương trình bậc nhất hai ẩn có đáp án (647 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 4. Các số đặc trưng đo mức độ phân tán của mẫu số liệu có đáp án (631 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1. Số gần đúng và sai số có đáp án (622 lượt thi)
