Trắc nghiệm Toán 10 Cánh diều Bài 2. Tập hợp. Các phép toán trên tập hợp (phần 2) có đáp án
Trắc nghiệm Toán 10 Bài 2. Tập hợp. Các phép toán trên tập hợp (Vận dụng) có đáp án
-
433 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho tập hợp C = {x ∈ ℝ| 8 < |– 3x + 5|}. Hãy viết lại các tập hợp C dưới dạng khoảng, nửa khoảng, đoạn.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có: \[8 < \left| { - 3x + 5} \right| \Leftrightarrow \left[ \begin{array}{l} - 3x + 5 > 8\\ - 3x + 5 < - 8\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > \frac{{13}}{3}\end{array} \right.\]
Mà C = {x ∈ ℝ| 8 < |– 3x + 5|}.
Do đó, C = {x ∈ ℝ| x < – 1 hoặc x > \(\frac{{13}}{3}\)} = \(\left( { - \infty ; - 1} \right) \cup \left( {\frac{{13}}{3}; + \infty } \right)\).
Câu 2:
19/07/2024Cho tập hợp \({C_\mathbb{R}}A = \left[ {0;6} \right)\), \({C_\mathbb{R}}B = \left( { - \frac{{12}}{3};5} \right) \cup \left( {\sqrt {17} ;\sqrt {55} } \right).\) Tập \({C_\mathbb{R}}\left( {A \cap B} \right)\)là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có:\[{C_\mathbb{R}}A = \left[ {0;6} \right) = \mathbb{R}\backslash A\], suy ra \[A = \left( { - \infty ;\,0} \right) \cup \left[ {6; + \infty } \right)\].
Lại có:\[{C_\mathbb{R}}B = \left( { - \frac{{12}}{3};5} \right) \cup \left( {\sqrt {17} ;\sqrt {55} } \right) = \left( { - \frac{{12}}{3};\,\sqrt {55} } \right) = \mathbb{R}\backslash B\]
(do \(\sqrt {17} = 4,123...\); \(\sqrt {55} = 7,416....\)).
Suy ra \[B = \left( { - \infty ; - \frac{{12}}{3}} \right] \cup \left[ {\sqrt {55} ; + \infty } \right).\]
Do đó, \[A \cap B = \left( { - \infty ; - \frac{{12}}{3}} \right] \cup \left[ {\sqrt {55} ; + \infty } \right)\]
\[ \Rightarrow {C_\mathbb{R}}\left( {A \cap B} \right) = \mathbb{R}\backslash \left( {A \cap B} \right) = \left( { - \frac{{12}}{3};\sqrt {55} } \right).\]
Câu 3:
20/07/2024Một lớp học có 23 học sinh giỏi môn Toán, 22 học sinh giỏi môn Lý, 15 học sinh
giỏi cả môn Toán và Lý và có 5 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Gọi A, B, C lần lượt là tập hợp các học sinh giỏi Toán, tập hợp các học sinh giỏi Lý và
tập học các học sinh không giỏi môn nào cả.
Theo bài ra ta có:
⦁ n(A) = 23;
⦁ n(B) = 22;
⦁ n(A ∩ B) = 15 (A ∩ B là tập hợp các học sinh giỏi cả môn Toán và môn Lý);
⦁ n(C) = 5.
Ta có biểu đồ Ven biểu diễn 3 tập hợp A, B, C như sau
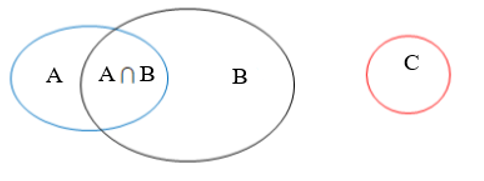
Từ biểu đồ ta thấy, số học sinh cả lớp là: n(A ∪ B) + n(C).
Lại có: n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 23 + 22 – 15 = 30.
Vậy số học sinh cả lớp là: 30 + 5 = 35 (học sinh).
Câu 4:
12/07/2024Cho A = {x ∈ ℝ| x + 2 ≥ 0}, B = {x ∈ ℝ| 5 – x ≥ 0}. Số các số nguyên thuộc cả hai tập A và B là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có A = {x ∈ ℝ| x + 2 ≥ 0} = {x ∈ ℝ| x ≥ – 2} = [– 2; + ∞).
B = {x ∈ ℝ| 5 – x ≥ 0} = {x ∈ ℝ| x ≤ 5} = (– ∞; 5].
Suy ra A ∩ B = [– 2; + ∞) ∩ (– ∞; 5] = [– 2; 5].
Các số nguyên thuộc cả hai tập A và B chính là các số nguyên thuộc tập A ∩ B, đó là các số: – 2; – 1; 0; 1; 2; 3; 4; 5.
Vậy có 8 số nguyên thuộc cả hai tập A và B.
Câu 5:
18/07/2024Cho hai tập khác rỗng E = (m – 1; 4] và F = (– 2; 2m + 2] với m ∈ ℝ. Xác định m để F ⊂ E.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
ĐKXĐ các tập E và F: \[\left\{ \begin{array}{l}m - 1 < 4\\2m + 2 > - 2\,\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m > - 2\,\end{array} \right. \Leftrightarrow - 2 < m < 5\].
Ta có: F ⊂ E (tập F là tập con của tập E)\[ \Leftrightarrow \left\{ \begin{array}{l}m - 1 \le - 2\\4 \ge 2m + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le - 1\\m \le 1\end{array} \right. \Leftrightarrow m \le - 1\].
Kết hợp với điều kiện ta được – 2 < m ≤ – 1.
Vậy m ∈ (– 2; 1].