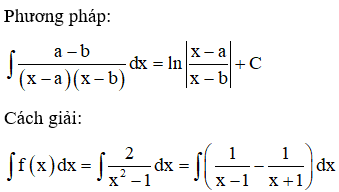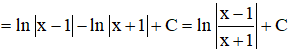Top 4 Đề thi Toán lớp 12 Học kì 1 chọn lọc, có đáp án
Đề thi Học kì 1 Toán 12 có đáp án (Đề 3)
-
2899 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
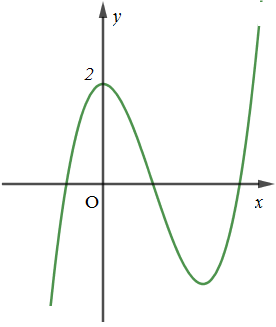
21/07/2024Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Nhận dạng đồ thị hàm số bậc ba
Cách giải:
Quan sát đồ thị hàm số ta thấy khi x → +∞ thì y → +∞ nên hệ số a > 0 ⇒ Loại phương án C và D
Mặt khác đồ thị hàm số đạt cực trị tại hai điểm: x = 0 và x = x0 > 0
![]()
![]()
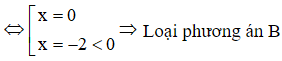
Ta chọn phương án A.
Câu 2:
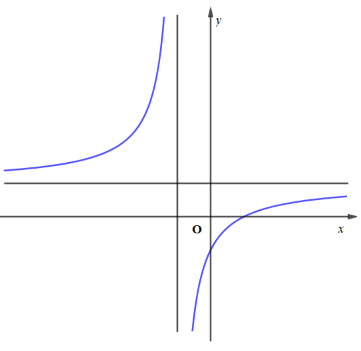
22/07/2024Cho hàm số có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Đồ thị hàm số có hai đường tiệm cận: x = c và y = a, đồng thời cắt trục hoành tại điểm
Cách giải:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng x = x0 < 0 ⇒ c < 0, đồ thị hàm số có tiệm cận ngang y = y_0 > 0 ⇒ a > 0
Đồ thị hàm số cắt trục hoành tại điểm
![]()
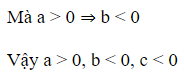
Câu 3:
15/07/2024Cho hàm số . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Hàm bậc nhất trên bậc nhất luôn đơn điệu trên từng khoảng xác định của nó.
Cách giải:
Hàm số bậc nhất trên bậc nhất không có giá trị nhỏ nhất.
Câu 4:
19/07/2024Tìm số giao điểm của đồ thị hàm số và đường thẳng y = 2x
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành đồ giao điểm của hai hàm số đó.
Cách giải:
Xét phương trình hoành độ giao điểm:
![]()
![]()
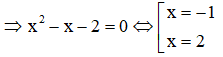
⇒ Số giao điểm của hai đồ thị hàm số là 2.
Câu 5:
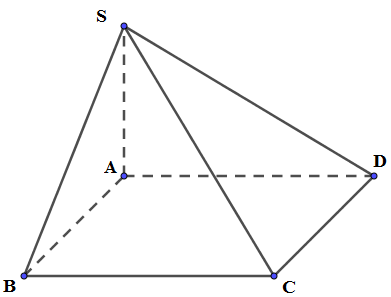
19/07/2024Cho hình chóp S.BACD có đáy ABCD là hình chữ nhật, . Cạnh bên và SA vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng công thức tính thể tích khối chóp:
Với: S là diện tích của đáy,
h là chiều cao của khối chóp.
Cách giải: .
Xét tam giác vuông ABC có:
![]()
Diện tích đáy ABCD:
![]()
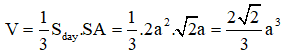
Câu 6:
23/07/2024Tìm giá trị lớn nhất M của hàm số trên đoạn [0;2]
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
- TXĐ
- Tính nghiệm và tìm các điểm không xác định ' y
- Tìm các giá trị tại x = 0, x = 2 và các điểm đã tìm ở trên (nằm trong đoạn đang xét) 0, 2 x x
- Xác định giá trị lớn nhất trong các giá trị đó.
Cách giải:
TXĐ: D = R
![]()
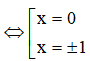
![]()
![]()
Câu 8:
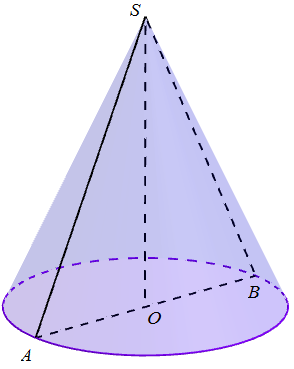
23/07/2024Một hình nón có chiều cao bằng a và thiết diện qua trục của hình nón đó là tam giác vuông. Tính theo a diện tích xung quanh của hình nón đó.
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Diện tích xung quanh của khối nón: Sxq = πRl
Cách giải:
Theo đề bài, ta có tam giác SAB là tam giác vuông cân tại S, SO = a ⇒ R = OA = SO = a

Câu 9:
19/07/2024Giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn lần lượt là
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và các điểm không xác định của y’ trên đoạn
Tính các giá trị tại và các điểm vừa tìm được
- Kết luận GTLN, GTNN của hàm số từ các giá trị trên.
Cách giải:
TXĐ: D = (0;+∞)
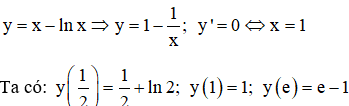
⇒ Giá trị nhỏ nhất, giá trị lớn nhất của hàm số lần lượt là: 1 và e - 1
Câu 10:
20/07/2024Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Tập xác định của hàm số y = xα:
+) Nếu α là số nguyên dương thì TXĐ: D = R
+) Nếu α là số nguyên âm hoặc bằng 0 thì TXĐ: D = R\{0}
+) Nếu α là số không nguyên thì TXĐ: D = (0;+∞)
Cách giải:
Hàm số xác định ⇔ x + 1 ≠ 0 ⇔ x ≠ -1
Vây tập xác định của hàm số y = (x + 1)-2 là R\{-1}
Câu 11:
16/07/2024Cho hình lăng trụ đứng có đáy ABC là tam giác cân tại A, . Tính theo a thể tích V của khối lăng trụ
 Xem đáp án
Xem đáp án
Đáp án D
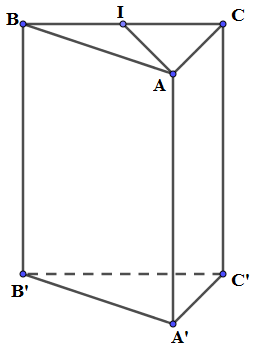
Phương pháp:
Thể tích khối lăng trụ: V = Sh, trong đó: S là diện tích đáy, h là chiều cao.
Cách giải:

Câu 12:
19/07/2024Cho hình hộp chữ nhật có . Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
 Xem đáp án
Xem đáp án
Đáp án C
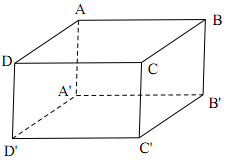
Phương pháp:
Thể tích khối hộp chữ nhật: V = abc
Cách giải:
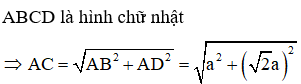
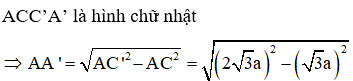
= 3a
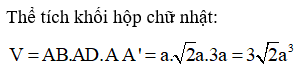
Câu 13:
19/07/2024Trong không gian với hệ tọa độ Oxyz, cho hai vectơ . Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp :
Thử lần lượt từng đáp án.
Cách giải:
![]()
![]()
Câu 14:
19/07/2024Trong không gian với hệ tọa độ Oxyz, cho các điểm Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp :
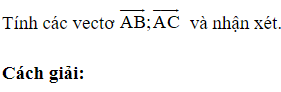
![]()
=> A, B, C thẳng hàng.
Câu 15:
22/07/2024Trong không gian với hệ tọa độ Oxyz, cho tam giác OAB có Tính độ dài đường cao kẻ từ O của tam giác OAB.
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Công thức khoảng cách từ điểm đến đường thẳng trong không gian:
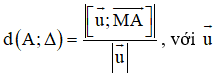 là VTCP của Δ và M là điểm bất kì thuộc
là VTCP của Δ và M là điểm bất kì thuộc
Cách giải:

Độ dài đường cao kẻ từ O của tam giác OAB bằng khoảng cách từ O đến đường thẳng AB:
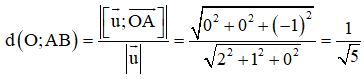
Câu 16:
19/07/2024Hàm số nào sau đây không đồng biến trên khoảng (-∞;+∞)
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
- Bước 1: Tìm tập xác định, tính f'(x)
- Bước 2: Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định
- Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
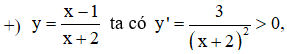
![]()
=> Hàm số đồng biến trên các khoảng (-∞;-2);(-2;+∞)
+) y = x3 + 2 ⇒ y'= 3x2 ≥ 0,∀ x∈R: Hàm số đồng biến trên R.
+) y = x + 1 ⇒ y' = 1 > 0, ∀ x∈R: Hàm số đồng biến trên R.
+) y = x5 + x3 - 1 ⇒ y' = 5x4 + 3x2 ≥ 0, ∀ x ∈ R; y' = 0 ⇔ x = 0 ⇒ Hàm số đồng biến trên R.
Câu 17:
20/07/2024Với a, b, c là các số thực dương, a và c khác 1 và α ≠ 0. Mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng các công thức liên quan đến logarit.
Cách giải:
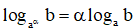
![]()
Câu 18:
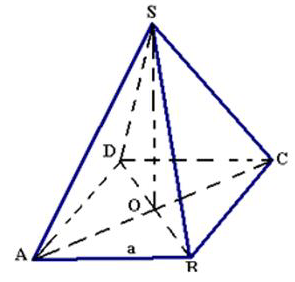
22/07/2024Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
- Xác định tâm I của đáy, dựng đường (d) vuông góc với mặt đáy tại I
- Dựng mặt phẳng trung trực (P) của cạnh SA
- Xác định giao tuyến O của mặt phẳng (P) và đường thẳng (d). O chính là tâm mặt cầu ngoại tiếp hình chóp.
Cách giải:
Gọi O là tâm của đáy ⇒ OA = OB = OC = OD(1)
Do hình chóp có tất cả các cạnh đều bằng nhau nên ΔSAC = ΔBAC ⇒ OS = OA = OC(2)
Từ (1), (2) ⇒ OA = OB = OC = OD = OS ⇒ Tâm mặt cầu ngoại tiếp hình chóp là tâm của mặt đáy ABCD.
Câu 19:
21/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, . Cạnh bên và SA vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.BCD.
 Xem đáp án
Xem đáp án
Đáp án B
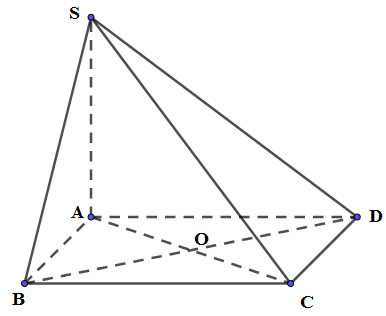
Phương pháp:
Thể tích khối chóp: V = Sh
Cách giải:

Câu 20:
15/07/2024Tìm mệnh đề đúng trong các mệnh đề sau
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Dựa vào hình dáng đồ thị hàm số mũ và tính đơn điệu của hàm số mũ.
Cách giải:
Đáp án A: Ví dụ đồ thị các hàm số
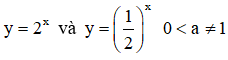
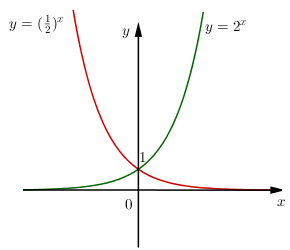
Chúng đối xứng nhau qua trục tung. Do đó đáp án A đúng.
Đáp án B và C hiển nhiên sai.
Đáp án D sai vì (a;1) thuộc đồ thị hàm số y = ax ⇔ 1 = aa không phải luôn đúng.
Câu 21:
22/07/2024Đường tiệm cận ngang của đồ thị hàm số là
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Đồ thị hàm số bậc nhất trên bậc nhất ,
![]() có tiệm cận đứng là tiệm cận ngang là
có tiệm cận đứng là tiệm cận ngang là
Cách giải:
Đường tiệm cận ngang của đồ thị hàm số
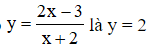
Câu 22:
21/07/2024Ông An gửi 100 triệu đồng vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất 8%/năm. Sau 5 năm ông rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại ông tiếp tục gửi vào ngân hàng với kỳ hạn và lãi suất như lần trước. Số tiền lãi mà ông An nhận được sau 10 năm gửi gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với:
An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%)
Cách giải:
Số tiền ông An rút lần 1 là: 100.(1 + 8%)5 = 146,9328077 (triệu đồng)
Số tiền ông An gửi lần 2 là: 146.9328077 : 2 = 73,46640384 (triệu đồng)
Số tiền ông An rút lần 2 (gửi 5 năm tiếp theo) là:
73,46640384.(1 + 8%)5 = 107,9462499 (triệu đồng)
Số tiền lãi là: 107,9462499 - 73,4660384 = 34,47984602 ≈ 34,480 (triệu đồng).
Câu 23:
20/07/2024Đạo hàm của hàm số y = xlnx trên khoảng (0;+∞) là
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp: (uv)' = u'v + uv'
Cách giải:
![]()
Câu 25:
20/07/2024Cho hàm số có bảng biến thiên như sau
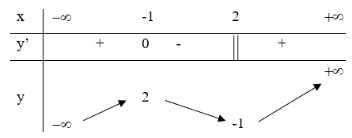
Mệnh đề nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Dựa vào bảng biến thiên.
Cách giải:
Dựa vào BBT ta dễ thấy hàm số đạt cực tiểu tại điểm x = 2 nên Đáp án C sai.
Câu 27:
20/07/2024Số đường tiệm cận ngang của đồ thị hàm số
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
* Định nghĩa tiệm cận ngang của đồ thị hàm số y = f(x)
![]()
=> y = a là tiệm cận ngang của đồ thị hàm số.
Cách giải:
TXĐ: D = R
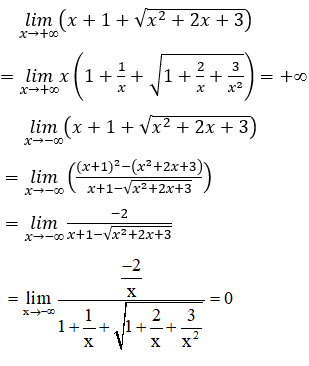
Vậy, đồ thị hàm số có tất cả 1 tiệm cận ngang là đường thẳng y=0
Câu 28:
23/07/2024Trong không gian với hệ tọa độ Oxyz, cho các vectơ Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án D
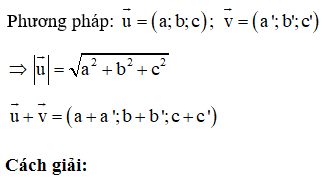
![]()
![]()
=> Đáp án A sai
+) => Đáp án D đúng
Câu 30:
19/07/2024Trong không gian với hệ tọa độ Oxyz, cho các điểm Góc giữa hai đường thẳng AB và AC bằng
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Đường thẳng d và d’ có các VTCP lần lượt là
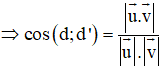

Câu 31:
21/07/2024Tập xác định của hàm số
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Hàm số y = lnx xác định ⇔ x > 0
Cách giải:
Điều kiện xác định: -x2 + 5x - 6 > 0 ⇔ 2 < x < 3
Vậy tập xác định của hàm số y = ln(-x2 + 5x - 6) là (2;3)
Câu 32:
19/07/2024Tìm số nghiệm nguyên của bất phương trình
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
- Tìm TXĐ
- Giải bất phương trình và tìm số nghiệm nguyên.
Cách giải:
Điều kiện xác định:
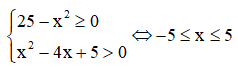
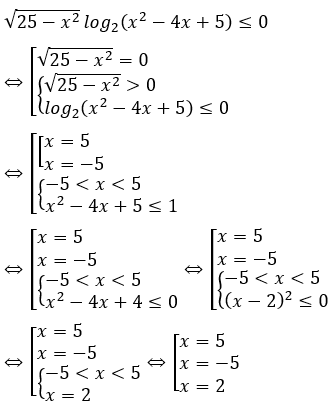
Vậy bất phương trình có 3 nghiệm nguyên.
Câu 33:
19/07/2024Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy A4 trong một giờ. Chi phí để bảo trì, vận hành một máy mỗi lần in là 50 nghìn đồng. Chi phí in ấn của n máy chạy trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50 000 bản in khổ A4 thì phải sử dụng bao nhiêu máy để thu được lãi nhiều nhất?
 Xem đáp án
Xem đáp án
Đáp án C
Cách giải:
Nhận xét: Để thu được nhiều lãi nhất thì tổng chi phí bảo trì, chi phí in ấn là ít nhất.
Gọi số máy in cần sử dụng là n (máy), n ∈ N; n ∈ (0;8)
Số giờ cần để in hết 50 000 bản in là: 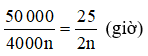
Chi phí để n máy hoạt động trong giờ là:
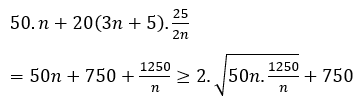
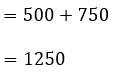
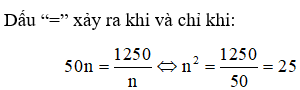
=> n = 5
Vậy, nếu in 50 000 bản in khổ A4 thì phải sử dụng 5 máy sẽ thu được lãi nhiều nhất.
Câu 34:
21/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng . Tính theo a thể tích V của khối chóp S.ABCD.
 Xem đáp án
Xem đáp án
Đáp án B
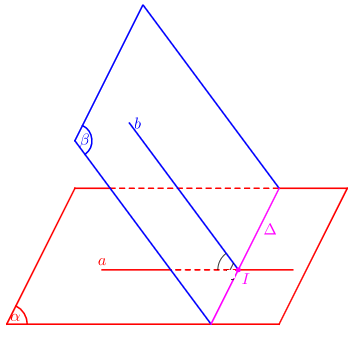
Phương pháp:
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
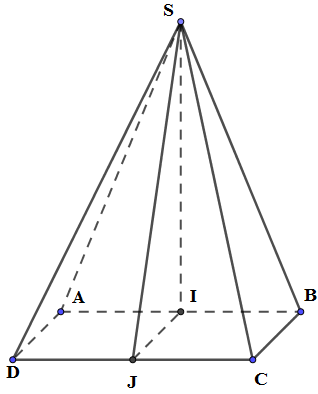
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
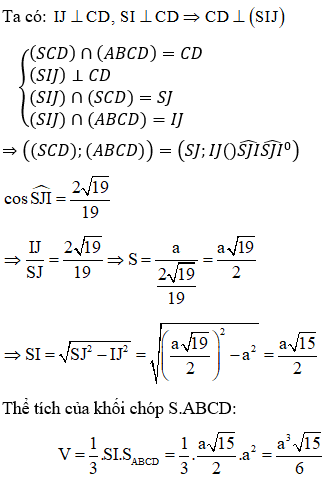
Câu 37:
21/07/2024Giá trị của tham số m để phương trình có 2 nghiệm thỏa mãn là
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:

Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8
Khi đó:
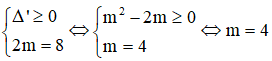
Câu 38:
22/07/2024Cho hàm số . Gọi F(x) là một nguyên hàm của f(x). Khẳng định nào sau là sai?
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
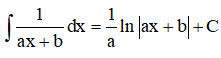
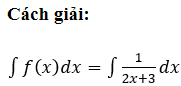
![]()
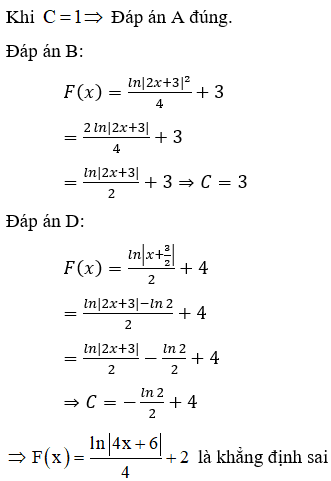
Câu 39:
20/07/2024Tìm tất cả các giá trị của tham số thực m để hàm số đạt cực tiểu tại điểm x = -1
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Hàm số bậc ba y = f(x) đạt cực tiểu tại x = x0 khi và chỉ khi
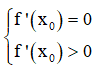
Cách giải:
![]()
![]()
![]()
![]()
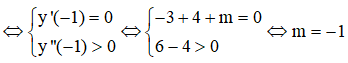
Câu 40:
11/07/2024Cho hàm số Số cực trị của hàm sốlà
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:

Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
![]()
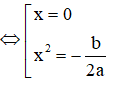
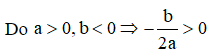
![]()
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7
Câu 41:
18/07/2024Số nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
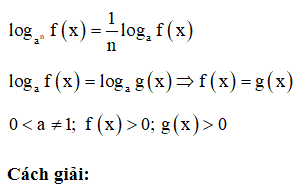
Điều kiện xác định:
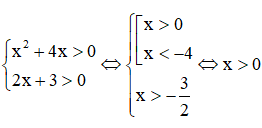
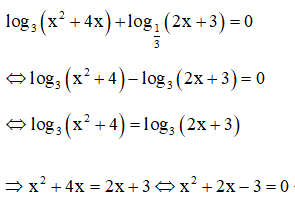
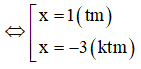
Vậy phương trình đã cho có 1 nghiệm là x = 1
Câu 42:
20/07/2024Nguyên hàm của f(x) = xcosx làa
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp: ∫udv = uv - ∫vdu
Cách giải:
F(x) = ∫f(x).dx = ∫x.cosx.dx = ∫x.dsinx = x.sinx - ∫sinx.dx = x.sinx + cosx + C
Câu 43:
23/07/2024Cho hàm số có đạo hàm Khi đó số cực trị của hàm số là
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Tính và xét dấu của f(x2)' từ đó tính số cực trị.
Cách giải:
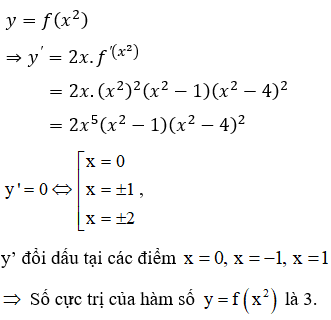
Câu 44:
11/07/2024Cho hình trụ có bán kính đáy bằng r, chiều cao bằng h. Khẳng định nào sai?
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Dựa vào các công thức tính diện tích toàn phần, diện tích xung quanh và thể tích của khối trụ.
Cách giải:
Diện tích toàn phần của hình trụ bằng 2πrh + 2πr2. Do đó đáp án A sai.
Câu 45:
20/07/2024Cho hàm số liên tục trên khoảng (a;b) và Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm khi và chỉ khi
(2) Nếu hàm số có đạo hàm và có đạo hàm cấp hai tại điểm thỏa mãn điều kiện thì điểm không phải là điểm cực trị của hàm số
(3) Nếu f'(x) đổi dấu khi x qua điểm thì điểm là điểm cực tiểu của hàm số
(4) Nếu hàm số có đạo hàm và có đạo hàm cấp hai tại điểm thỏa mãn điều kiện thì điểm là điểm cực tiểu của hàm số
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
Câu 46:
23/07/2024Cho hình chóp S.ABCD có đáy là hình vuông, hình chiếu của S lên (ABCD) là điểm H thuộc cạnh AB thỏa mãn góc giữa SC và (ABCD) bằng 60°. Biết rằng khoảng cách từ A đến (SCD) bằng . Thể tích V của khối chóp S.ABCD là
 Xem đáp án
Xem đáp án
Đáp án C
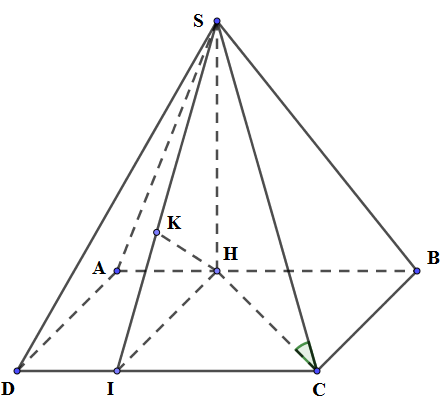
Phương pháp:
+) d(A;(SCD)) = d(H;(SCD)) xác định khoảng cách từ H đến (SCD).
+) Xác định góc giữa SC và mặt đáy.
+) Đặt cạnh của hình vuông ở đáy là x, tính SH và HI theo x.
+) Sử dụng hệ thức lượng trong tam giác vuông để tìm x.
![]()
Cách giải:
![]()
![]()
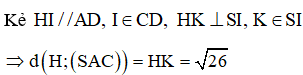
Giả sử độ dài cạnh hình vuông ở đáy là x. Khi đó, HI = x
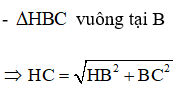
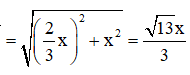
![]()
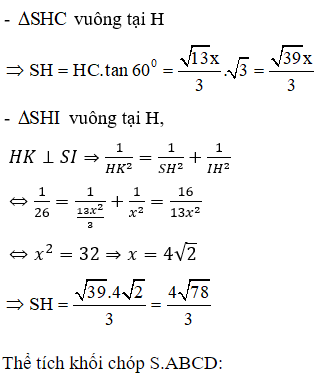

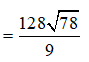
Câu 47:
21/07/2024Cho hình nón đỉnh S, đáy là đường tròn (O; r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho . Tính theo r khoảng cách từ O đến (SAB).
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
+) Xác định khoảng cách từ O đến (SAB)
+) Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách vừa xác định được.
Cách giải:
Gọi I là trung điểm của AB, kẻ OH vuông góc SI tại H.
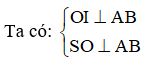
![]()
![]()
![]()
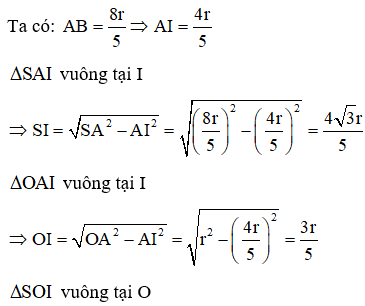
![]()
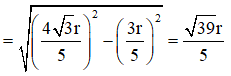
ΔSOI vuông tại O, OH ⊥ SI ⇒ OH.SI = SO.OI
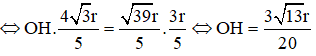
Câu 49:
21/07/2024Tìm m để phương trình có 2 nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
![]()
+) Vẽ hai đồ thị hàm số trên cùng hệ trục tọa độ và biện luận.
Cách giải:
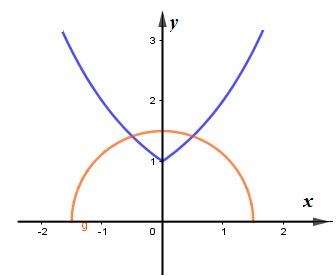
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số ![]()
![]() có đồ thị là nửa đường tròn x2 + y2 = m2 (phần nằm phía trên trục hoành)
có đồ thị là nửa đường tròn x2 + y2 = m2 (phần nằm phía trên trục hoành)
Quan sát đồ thị, ta thấy: để 2 đồ thị cắt nhau tại 2 điểm phân biệt thì bán kính của đường tròn x2 + y2 = m2 phải lớn hơn 1
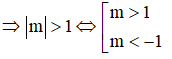
Câu 50:
11/07/2024Số giá trị nguyên của tham số m để phương trình có ba nghiệm phân biệt là
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
![]()
+) Thế vào phương trình, lập phương hai vế, cô lập m, đưa phương trình về dạng m = f(t)
+) Khảo sát và lập BBT của hàm số y = f(t), t ≥ 0 Biện luận để phương trình có 2 nghiệm phân biệt.
Cách giải:
![]()

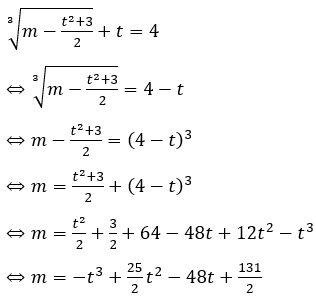
![]()
![]()
Ta có:
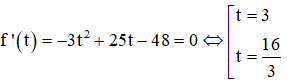
Bảng biến thiên:
Để phương trình có 3 nghiệm phân biệt t ≥ 0 thì ![]()
⇒ Có 6 giá trị nguyên của m thỏa mãn.
Bài thi liên quan
-
Đề thi Học kì 1 Toán 12 có đáp án (Đề 1)
-
50 câu hỏi
-
90 phút
-
-
Đề thi Học kì 1 Toán 12 có đáp án (Đề 2)
-
50 câu hỏi
-
90 phút
-
-
Đề thi Học kì 1 Toán 12 có đáp án (Đề 4)
-
50 câu hỏi
-
90 phút
-
Có thể bạn quan tâm
- Đề kiểm tra 1 tiết Giải tích 12 Chương 1 có đáp án (419 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án (2249 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 chương 2 có đáp án (290 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 2 Giải tích có đáp án (2256 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 1 Hình học có đáp án (3504 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 2 Hình học có đáp án (2487 lượt thi)
- Top 4 Đề thi Toán lớp 12 Học kì 1 chọn lọc, có đáp án (2898 lượt thi)
Các bài thi hot trong chương
- Top 8 Đề kiểm tra Toán 12 Chương 3 Hình học có đáp án (2230 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 3 Giải tích có đáp án (2107 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 4 Giải tích có đáp án (1689 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 Chương 3 có đáp án (387 lượt thi)
- Đề thi Học kì 2 Giải tích 12 có đáp án (319 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 Chương 4 có đáp án (300 lượt thi)