Câu hỏi:
21/07/2024 205Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
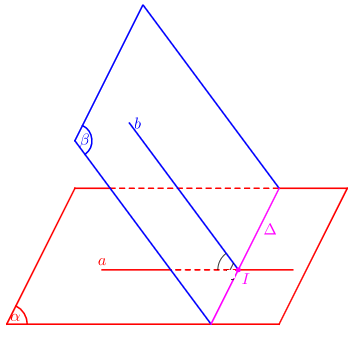
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
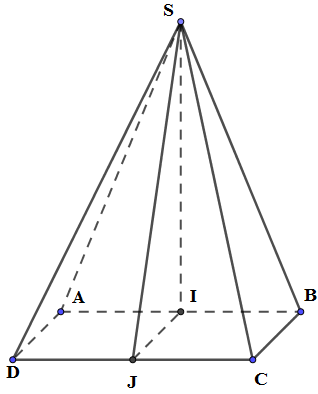
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho tam giác OAB có Tính độ dài đường cao kẻ từ O của tam giác OAB.
Câu 2:
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Khẳng định nào đúng?
Câu 4:
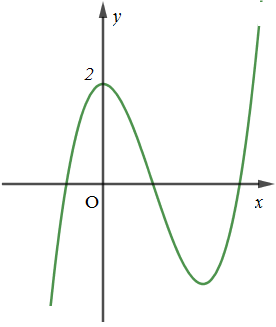
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Câu 8:
Một hình nón có chiều cao bằng a và thiết diện qua trục của hình nón đó là tam giác vuông. Tính theo a diện tích xung quanh của hình nón đó.
Câu 9:
Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy A4 trong một giờ. Chi phí để bảo trì, vận hành một máy mỗi lần in là 50 nghìn đồng. Chi phí in ấn của n máy chạy trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50 000 bản in khổ A4 thì phải sử dụng bao nhiêu máy để thu được lãi nhiều nhất?
Câu 13:
Cho hàm số có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
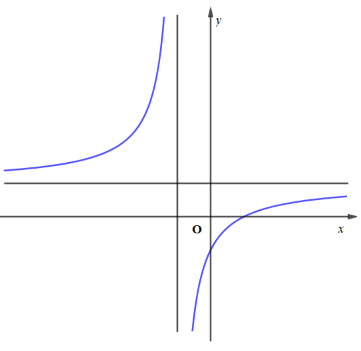
Câu 14:
Cho hình nón đỉnh S, đáy là đường tròn (O; r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho . Tính theo r khoảng cách từ O đến (SAB).
Câu 15:
Trong không gian với hệ tọa độ Oxyz, cho các vectơ Khẳng định nào đúng?


