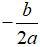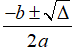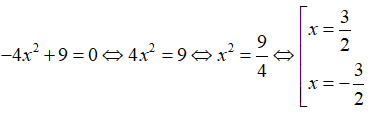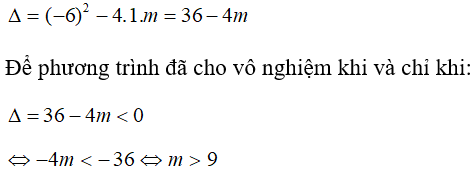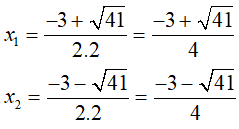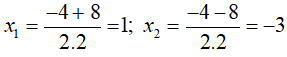Trắc nghiệm Toán 9 Bài 4 (có đáp án): Công thức nghiệm của phương trình bậc hai
-
816 lượt thi
-
10 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 2:
03/07/2024Cho phương trình a + bx + c = 0 (a 0) có biệt thức = - 4ac. Phương trình đã cho vô nghiệm khi:
Xem đáp án
Đáp án A
Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac
• TH1: Nếu thì phương trình vô nghiệm
• TH2: Nếu thì phương trình có nghiệm kép x1 = x2 = 
• TH3: Nếu thì phương trình có hai nghiệm phân biệt x1,2 = 
Câu 3:
19/07/2024Cho phương trình a + bx + c = 0 (a0) có biệt thức = - 4ac > 0. Khi đó phương trình có hai nghiệm phân biệt là:
Xem đáp án
Đáp án C
Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức Δ = b2 - 4ac
• TH1: Nếu thì phương trình vô nghiệm
• TH2: Nếu thì phương trình có nghiệm kép x1 = x2 =
• TH3: Nếu thì phương trình có hai nghiệm phân biệt x1,2 =
Câu 4:
03/07/2024Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6 - 7x = 0
Xem đáp án
Đáp án B
Câu 5:
13/07/2024Không dùng công thức nghiệm, tìm số nghiệm của phương trình -4 + 9 = 0
Xem đáp án
Đáp án D
Câu 6:
15/07/2024Cho phương trình – 6x + m = 0. Tìm m để phương trình đã cho vô nghiệm?
Xem đáp án
Đáp án A
Câu 7:
15/07/2024Cho phương trình (m + 1) + 4x + 1 = 0. Tìm m để phương trình đã cho có nghiệm
Xem đáp án
Đáp án D
* Với m = -1 thì phương trình đã cho trở thành: 4x + 1 = 0 x = -1/4
Do đó, m = -1 thỏa mãn điều kiện.
* Nếu m -1 , khi đó phương trình đã cho là phương trình bậc hai một ẩn.
Ta có: = - 4.(m + 1).1 = 16 - 4m - 4 = 12 - 4m
Để phương trình đã cho có nghiệm khi: = 12 - 4m 0
-4m - 12 ⇔ m 3
Kết hợp 2 trường hợp, để phương trình đã cho có nghiệm thì m 3.
Câu 8:
15/07/2024Cho phương trình 2 + 3x – 4 = 0 . Tìm mệnh đề sai trong các mệnh đề sau?
Xem đáp án
Đáp án C
Ta có: = 9 + 32 = 41 > 0
Do đó, phương trình đã cho có 2 nghiệm phân biệt là:
Ta thấy các nghiệm đều không nguyên
Vậy C sai.
Câu 9:
23/07/2024Trong các phương trình sau, phương trình nào có nghiệm duy nhất.
Xem đáp án
Đáp án D
Ta tính ∆ của các phương trình đã cho:
A. ∆ = (-4)2 - 4.1.10 = 16 – 40 = 24 > 0 nên phương trình này có hai nghiệm phân biệt
B. ∆ = 42 -4.(-2).4 = 16 + 32 = 48 > 0 nên phương trình này có hai nghiệm phân biệt.
C. ∆ = 02 – 4. (-3). 9 = 0 + 108 = 108 > 0 nên phương trình này có hai nghiệm phân biệt.
D. ∆ = (-4)2 - 4.4.1 = 0 nên phương trình này có nghiệm duy nhất
Câu 10:
03/07/2024Tìm giao điểm của đồ thị hàm số y = 2 và đường thẳng y = - 4x + 6
Xem đáp án
Đáp án A
Hoành độ giao điểm của parabol và đường thẳng đã cho là nghiệm phương trình:
2 = -4x + 62 + 4x - 6 = 0 (*)
Phương trình này có = - 4.2.(-6) = 16 + 48 = 64
Do đó, phương trình (*) có hai nghiệm phân biệt:
Với x = 1 thì y = -4. 1 + 6 = 2 ta được điểm A(1; 2).
Với x = -3 thì y = -4.(-3) + 6 = 18 ta được điểm B( -3; 18)
Vậy parabol cắt đường thẳng tại hai điểm là A( 1;2) và B(- 3 ; 18)