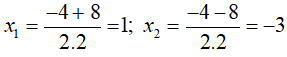Câu hỏi:
03/07/2024 171Tìm giao điểm của đồ thị hàm số y = 2x2 và đường thẳng y = - 4x + 6
A. A(1; 2) và B(- 3; 18)
B. A(1; 2) và B(3; -6)
C. A( 3; -6) và B( -1; 10)
D. Đáp án khác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Hoành độ giao điểm của parabol và đường thẳng đã cho là nghiệm phương trình:
2x2 = -4x + 6⇔2x2 + 4x - 6 = 0 (*)
Phương trình này có △ = 42 - 4.2.(-6) = 16 + 48 = 64
Do đó, phương trình (*) có hai nghiệm phân biệt:
Với x = 1 thì y = -4. 1 + 6 = 2 ta được điểm A(1; 2).
Với x = -3 thì y = -4.(-3) + 6 = 18 ta được điểm B( -3; 18)
Vậy parabol cắt đường thẳng tại hai điểm là A( 1;2) và B(- 3 ; 18)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho phương trình 2x2 + 3x – 4 = 0 . Tìm mệnh đề sai trong các mệnh đề sau?
Câu 2:
Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6x2 - 7x = 0
Câu 4:
Cho phương trình ax2 + bx + c = 0 (a≠0) có biệt thức △ = b2 - 4ac > 0. Khi đó phương trình có hai nghiệm phân biệt là:
Câu 5:
Cho phương trình x2 – 6x + m = 0. Tìm m để phương trình đã cho vô nghiệm?
Câu 6:
Không dùng công thức nghiệm, tìm số nghiệm của phương trình -4x2 + 9 = 0
Câu 7:
Cho phương trình (m + 1)x2 + 4x + 1 = 0. Tìm m để phương trình đã cho có nghiệm
Câu 9:
Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức △ = b2 - 4ac. Phương trình đã cho vô nghiệm khi: