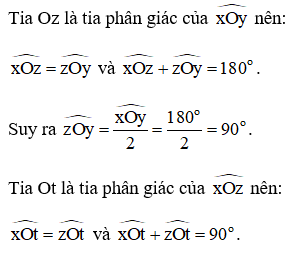Bài tập Tia phân giác có đáp án
-
329 lượt thi
-
14 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
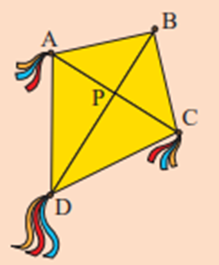
21/07/2024Khi làm con diều như hình bên thì tia DB nằm ở vị trí nào của ^ADC?
 Xem đáp án
Xem đáp án
Trong hình trên, tia DB xuất phát từ đỉnh D của ^ADC, đi qua điểm B nằm trong ^ADC.
Câu 2:
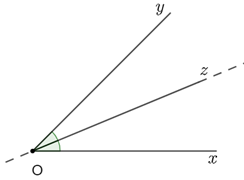
21/07/2024Vẽ ^xOy lên một tờ giấy như Hình 1a. Gấp giấy sao cho cạnh Oy trùng với cạnh Ox. Nếu gấp cho ta vị trí của Oz. Theo em tia Oz đã chia ^xOy thành hai góc như thế nào?
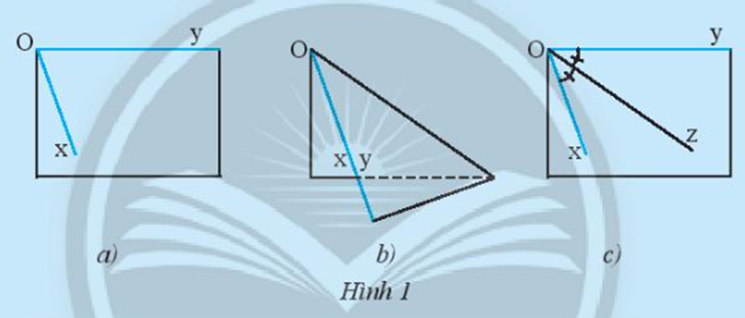
 Xem đáp án
Xem đáp án
Thực hiện gấp giấy theo các bước ở đề bài.
Theo em tia Oz đã chia ^xOy thành hai góc bằng nhau.
Câu 3:
17/07/2024Tìm tia phân giác của các góc: ^AOC và ^COB trong Hình 3.
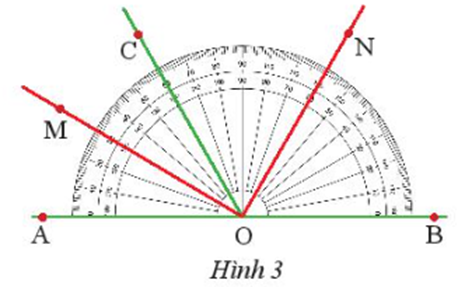
 Xem đáp án
Xem đáp án
- Tia OM xuất phát từ đỉnh O của ^AOC , đi qua điểm M nằm trong ^AOC và ^AOM=^COM=30o .
Do đó, OM là tia phân giác của ^AOC.
- Tia ON xuất phát từ đỉnh O của ^COB , đi qua điểm N nằ m trong ^COB và ^BON=^CON=60o .
Do đó, ON là tia phân giác của ^COB.
Vậy OM là tia phân giác của ^AOC; ON là tia phân giác của ^COB.Câu 4:
17/07/2024Em hãy cho biết khi cân thăng bằng thì kim ở vị trí nào của ^AOB (Hình 4).
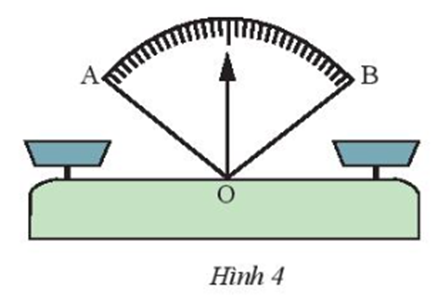
 Xem đáp án
Xem đáp án
Ta lấy điểm M bất kì nằm trên kim cân (như hình vẽ).
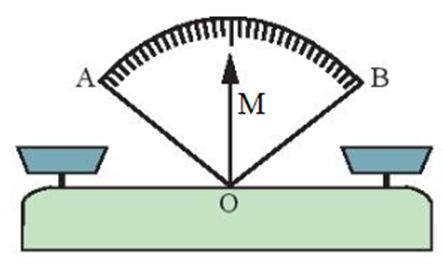
Kim của chiếc cân là tia xuất phát từ đỉnh O của góc AOB, đi qua điểm M nằm trong góc AOB.
Và cân thăng bằng khi ^AOM=^BOM.
Do đó, OM là tia phân giác của góc AOB.
Vậy khi cân thăng bằng thì kim là tia phân giác của ^AOB.
Câu 5:
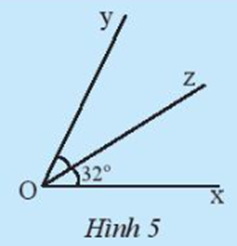
17/07/2024Trong Hình 5, nếu Oz là tia phân giác của ^xOy thì số đo của ^xOy bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Vì Oz là tia phân giác của ^xOy nên ^xOz=^yOz=32o .
Mặt khác, Oz là tia phân giác của nên tia Oz cũng nằm giữa hai tia Ox và Oy.
Khi đó, ^xOy=^xOz+^yOz .
Suy ra ^xOy=32o+32o=64o .
Vậy nếu Oz là tia phân giác của ^xOy thì ^xOy=64o .
Câu 6:
17/07/2024Vẽ một góc có số đo bằng 60o rồi vẽ tia phân giác của góc đó.
 Xem đáp án
Xem đáp án
Giả sử ^xOy=60o , vẽ tia Oz là tia phân giác của ^xOy .
Cách vẽ:
- Vẽ ^xOy=60o.
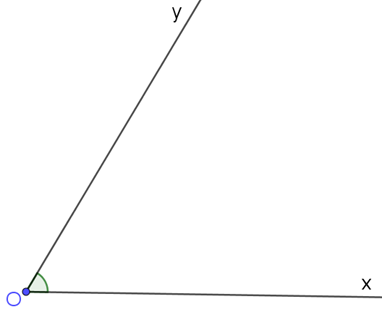
- Ta có ^xOz=^yOz và ^xOz+^yOz=60o .
Suy ra ^xOz=^xOy2=60o2=30o.
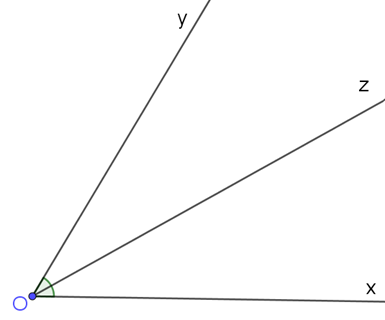
- Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của ^xOy sao cho^xOz=30o.
Ta được tia Oz là phân giác của ^xOy.
Câu 7:
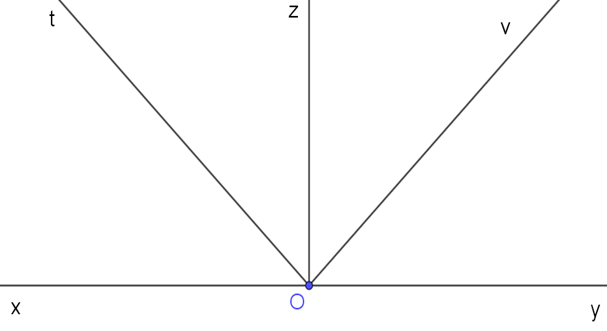
20/07/2024Hãy vẽ một góc bẹt ^AOB rồi vẽ tia phân giác của góc đó.
 Xem đáp án
Xem đáp án
Giả sử vẽ tia OM là tia phân giác của ^AOB .
Cách vẽ:
Bước 1:
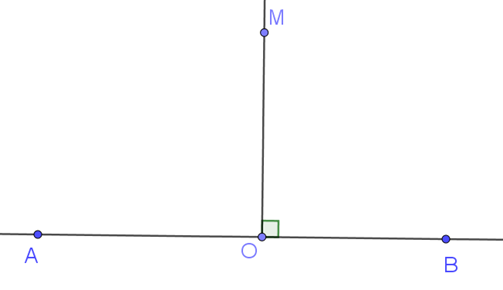
+ Vẽ đường thẳng AB. Lấy điểm O nằm giữa hai điểm A và B.

+ Ta có ^AOM=^BOM và ^AOM+^BOM=180o .
Suy ra ^AOM=^AOB2=180o2=90o .
Bước 2:
- Cách 1: Dùng thước đo góc vẽ tia OM đi qua điểm M nằm trong ^AOB sao cho ^AOM=90o.
- Cách 2: Dùng thước ê ke kẻ OM vuông góc với OA.
Ta được tia OM là phân giác của ^AOB.
Chú ý: Góc bẹt có hai tia phân giác là hai tia đối nhau.
Câu 8:
17/07/2024a) Trong Hình 8, tìm tia phân giác của các góc ^ABC, ^ADC.
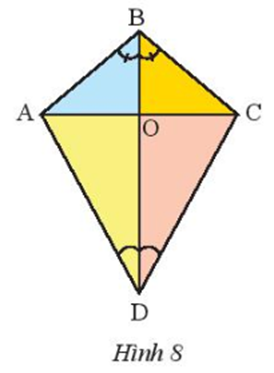
b) Cho biết ^ABC=100o, ^ADC=60o. Tính số đo của các góc ^ABO, ^ADO.
 Xem đáp án
Xem đáp án
a) Tia BO xuất phát từ đỉnh B của ^ABC , đi qua điểm O nằm trong ^ABC và ^ABO=^CBO .
Do đó, BO là tia phân giác của ^ABC.
Tia DO xuất phát từ đỉnh D của ^ADC, đi qua điểm B nằm trong ^ADC và ^ADO=^CDO.
Do đó, DO là tia phân giác của ^ADC.
Vậy BO và DO lần lượt là tia phân giác của các góc ^ABC, ^ADC .
b) Vì BO là tia phân giác của nên:
^ABO=^CBO=^ABC2=100o2=50o.
Vì BO là tia phân giác của nên:
^ADO=^CDO=^ADC2=60o2=30o.
Vậy ^ABO=50o;
Câu 9:
23/07/2024a) Vẽ có số đo 110o.
b) Vẽ tia phân giác của trong câu a.
 Xem đáp án
Xem đáp án
a) Các bước vẽ có số đo 110o:
Bước 1: Vẽ tia Ox bất kì. Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.
Bước 2: Xoay thước sao cho một cạnh Ox của góc đi qua vạch 0 của thước và thước chồng lên phần trong của góc.
Bước 3: Tại vạch chỉ số 110 trên thước đo góc, chấm một chấm nhỏ. Nối điểm đó với điểm O.
Ta được có số đo 110o.
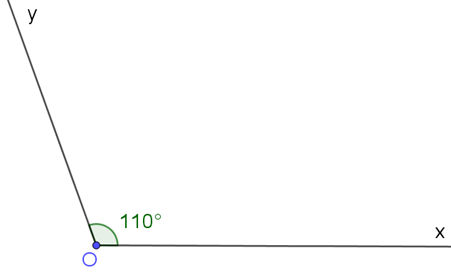
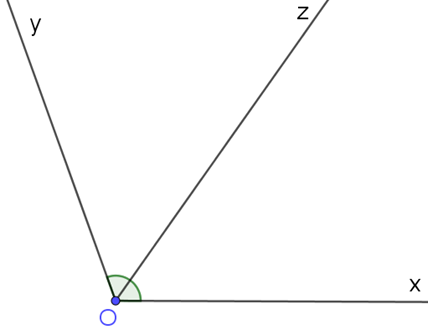
b) Giả sử Oz là tia phân giác của trong câu a.
Khi đó và .
Suy ra .
- Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của sao cho .
Ta được tia Oz là phân giác của .
Câu 10:
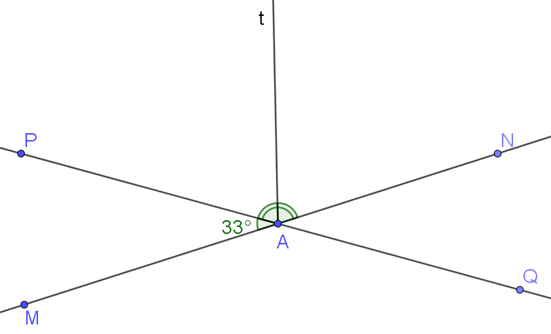
17/12/2024Cho hai đường thẳng MN, PQ cắt nhau tại A và tạo thành (Hình 9).
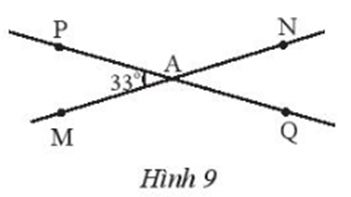
a) Tính số đo các góc còn lại.
b) Vẽ At là tia phân giác của . Hãy tính số đo của . Vẽ tia At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của Xem đáp án
Xem đáp án
Lời giải
Thiếu số thứ tự ý a
a) Vì và là hai góc kề bù nên:
Suy ra .
Mặt khác, (hai góc đối đỉnh)
(hai góc đối đỉnh).
Vậy số đo các góc còn lại là:
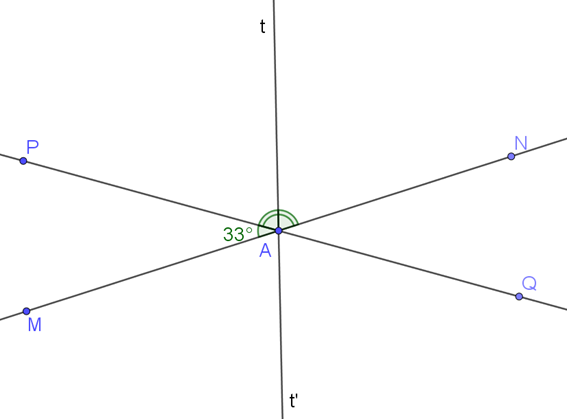
b) Vẽ tia At là tia phân giác của (như hình vẽ):


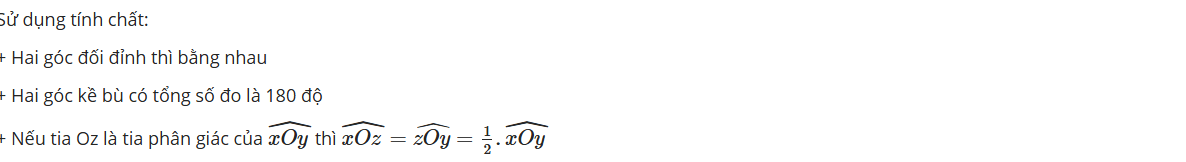
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Khi hai đường thẳng a và b cắt nhau, chúng tạo thành các cặp góc đối đỉnh như minh họa trong hình vẽ.
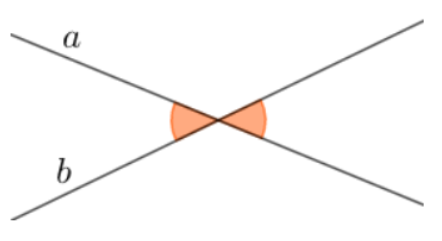
Còn có một cặp góc đối đỉnh khác:
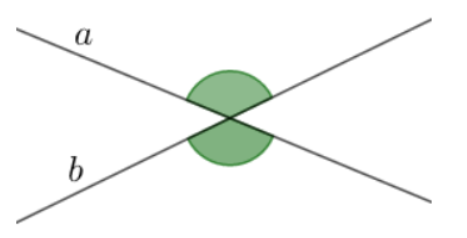
Khi hai đường thẳng cắt nhau, chúng tạo ra hai cặp góc đối đỉnh.
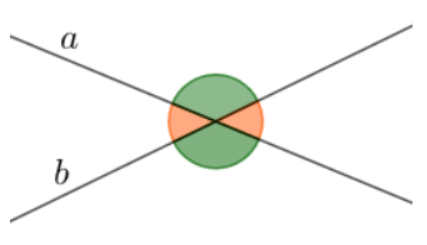
2. Tính chất của hai góc đối đỉnh
- Hai góc đối đỉnh luôn bằng nhau
Hai góc kề bù là hai góc có chung một cạnh và hai cạnh còn lại nằm trên hai tia đối nhau. Tổng số đo của hai góc kề bù bằng 180 độ.
Ví dụ:
Hai góc , là hai góc kề nhau, do chúng có cạnh chung là cạnh An và tổng số đo của chúng bằng 180 độ.
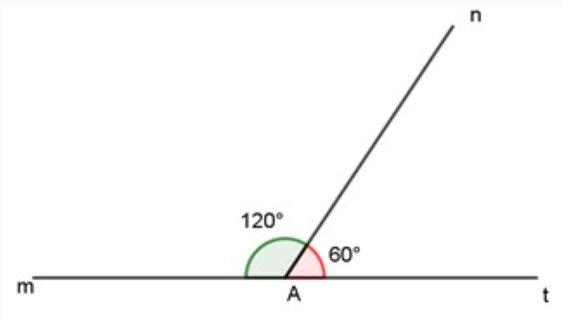
2. Tính chất và cách nhận biết hai góc kề bù
Tính chất hai góc kề bù:
-
Có một cạnh chung.
-
Hai cạnh còn lại nằm trên hai tia đối nhau.
-
Tổng số đo của hai góc bằng 180 độ.
Cách nhận biết hai góc kề bù:
-
Kiểm tra xem hai góc có chung một cạnh hay không.
-
Kiểm tra xem hai cạnh còn lại có nằm trên hai tia đối nhau hay không.
-
Kiểm tra xem tổng số đo của hai góc có bằng 180 độ hay không.
Suy ra
Câu 11:
08/11/2024Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho . Vẽ tia Ot sao cho và Gọi Ov là tia phân giác của . Các góc và có phải là hai góc đối đỉnh không? Vì sao?
 Xem đáp án
Xem đáp án
*Lời giải:
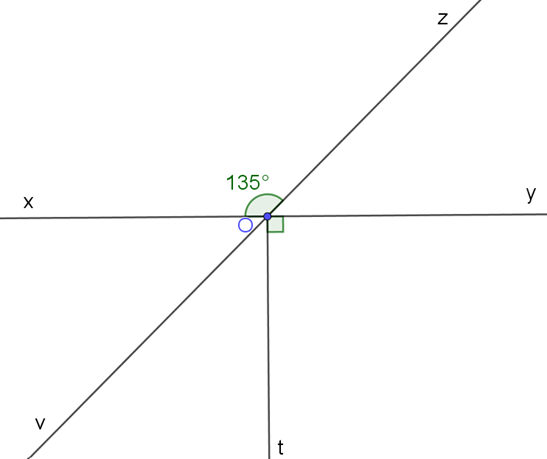
Vì mà là góc bẹt nên .
Tia Ov là tia phân giác của nên:
và
Suy ra
Tia Ox nằm giữa hai tia Oz và Ov nên:
Suy ra
Khi đó, tia Oz và Ov là hai tia đối nhau.
Mặt khác, đường thẳng xy đi qua điểm O nên Ox và Oy là hai tia đối nhau.
Do đó, tia Ox của là tia đối của tia Oy của
Vậy và là hai góc đối đỉnh.
*Phương pháp giải:
Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
Khi Oz là tia phân giác của góc thì .
* Các lý thuyết thêm và các dạng bài toán về tia phân giác:
Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
Khi Oz là tia phân giác của góc ˆxOythì ˆxOz=ˆzOy=12ˆxOy.
Định lí tia phân giác
* Định lý thuận:
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
* Định lí đảo:
- Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
- Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
Đường phân giác
1. Đường phân giác là gì?
- Đường phân giác của một góc chia góc đó thành hai góc có độ lớn bằng nhau.
- Mọi điểm trên một đường phân giác cách đều hai cạnh của góc đó và ngược lại.
2. Tính chất đường phân giác trong tam giác
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
* Lưu ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
Sự khác biệt giữa tia phân giác và đường phân giác
Tia Phân Giác: Là một tia bắt đầu từ đỉnh của một góc và chia góc đó thành hai góc bằng nhau. Tia phân giác không phải là đoạn thẳng có độ dài xác định mà là một phần của đường thẳng vô hạn.
Đường Phân Giác: Trong một tam giác, đường phân giác là đoạn thẳng nối từ một đỉnh tam giác đến điểm cắt của tia phân giác với cạnh đối diện. Đường phân giác là một đoạn thẳng có độ dài xác định và chia cạnh đối diện tam giác theo tỷ lệ nhất định.
Mối Quan Hệ: Tia phân giác là thành phần cơ bản có thể dựa vào từ đó xác định đường phân giác. Đường phân giác chính là đoạn thẳng mà tia phân giác cắt cạnh đối diện tam giác, và nó chia cạnh đối diện thành hai phần tương ứng.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Tia phân giác – Toán lớp 7 Chân trời sáng tạo
Toán 7 Bài 2 (Chân trời sáng tạo) giải vở bài tập: Tia phân giác
Trắc nghiệm Tính chất tia phân giác của một góc có đáp án - Toán lớp 7
Câu 12:
23/07/2024Vẽ hai góc kề bù , , biết . Gọi Oz là tia phân giác của . Tính .
 Xem đáp án
Xem đáp án

Vì là hai góc kề bù nên:
Suy ra .
Tia Oz là tia phân giác của nên:
Suy ra .
Tia Oy nằm giữa hai tia Ox’ và Oz nên:
Do đó .
Vậy .Câu 13:
23/07/2024Vẽ hai góc kề bù biết . Gọi Oz là tia phân giác của , Oz’ là tia phân giác của . Tính .
 Xem đáp án
Xem đáp án
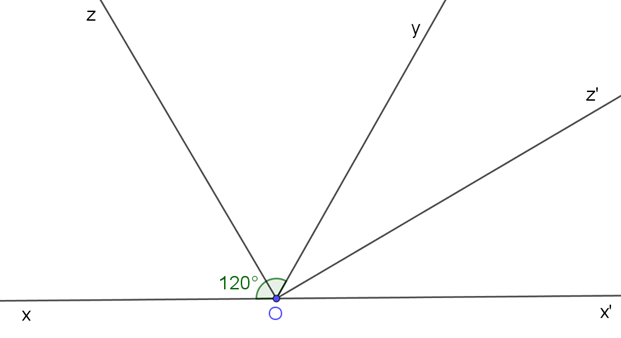
và là hai góc kề bù nên:
Suy ra .
Tia Oz là tia phân giác của nên:
và .
Suy ra .
Tia Oz’ là tia phân giác của nên:
Suy ra .
Ta có:
Vậy .