Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học
Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học (P1) (Đề 3)
-
690 lượt thi
-
29 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Thiết diện qua trục của hình nón tròn xoay là một tam giác đều cạnh 2a. Tính thể tích V của khối nón đó.
 Xem đáp án
Xem đáp án
Chọn B
Câu 2:
13/07/2024Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
 Xem đáp án
Xem đáp án
Chọn C

Câu 3:
22/07/2024Cho lăng trụ tam giác đều, có độ dài tất cả các cạnh bằng 2. Tính thể tích V của khối lăng trụ đó.
 Xem đáp án
Xem đáp án
Chọn A
Câu 4:
22/07/2024Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB = a; SA = SB = a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
 Xem đáp án
Xem đáp án
Chọn B
Câu 5:
19/07/2024Cho hình trụ có bán kính đáy bằnga√2. Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng a2 ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
 Xem đáp án
Xem đáp án
Chọn C
Câu 6:
13/07/2024Cho hình nón có bán kính đáy bằng a và diện tích toàn phần bằng 3πa2. Độ dài đường sinh l của hình nón bằng:
 Xem đáp án
Xem đáp án
Chọn C
Câu 8:
17/07/2024Cho khối lăng trụ ABC.A'B'C' có diện tích đáy ABC bằng S và chiều cao bằng h. Thể tích của khối lăng trụ đã cho bằng:
 Xem đáp án
Xem đáp án
Chọn D
Câu 9:
21/07/2024Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên (SBC) vuông góc với đáy và ^CSB=90o . Tính theo a bán kính mặt cầu ngoại tiếp chóp S.ABC?
 Xem đáp án
Xem đáp án
Chọn C
Câu 10:
18/07/2024Thể tích V của khối trụ có bán kính đáy r = 4 và chiều cao h= 4√2 là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 11:
21/07/2024Thể tích của khối nón có đường sinh bằng 10 và bán kính đáy bằng 6 là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 12:
13/07/2024Cho mặt cầu tâm O và tam giác ABC có ba đỉnh nằm trên mặt cầu với góc ^BAC=30o và BA = a. Gọi S là điểm nằm trên mặt cầu, không thuộc mặt phẳng (ABC) và thỏa mãn SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60o. Tính thể tích V của khối cầu tâm O theo a.
 Xem đáp án
Xem đáp án
Chọn B
Câu 13:
13/07/2024Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của một hình nón. Tính diện tích xung quanh Sxq của hình nón đó theo l,h,r.
 Xem đáp án
Xem đáp án
Chọn D
Câu 14:
22/07/2024Một khối trụ có thể tích bằng 25π .Nếu chiều cao hình trụ tăng lên năm lần và giữa nguyên bán kính đáy thì được một hình trụ mới có diện tích xung quanh bằng 25π. Tính bán kính đáy r của hình trụ ban đầu.
 Xem đáp án
Xem đáp án
Chọn C
Câu 15:
13/07/2024Trong không gian cho tam giác OIM vuông tại I, góc ^IOM=45ovà cạnh IM = a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Tính diện tích xung quanh Sxq của hình nón tròn xoay đó theo a
 Xem đáp án
Xem đáp án
Chọn A
Câu 16:
13/07/2024Cho khối nón có bán kính đáy r = 3, chiều cao h=√2 Tính thể tích V của khối nón.
 Xem đáp án
Xem đáp án
Chọn B
Câu 17:
19/07/2024Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 18:
03/12/2024Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 4π. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Lời giải
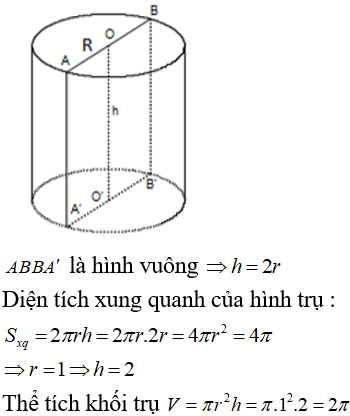
*Phương pháp giải:
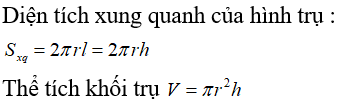
*Lý thuyết:
Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.
- Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.
- Đường thẳng AB được gọi là trục của hình trụ.
- Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.
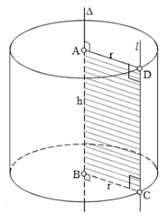
- Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.
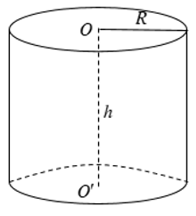
Cho hình trụ có bán kính đáy R và chiều cao h.
- Diện tích xung quanh: Sxq = 2πRh.
- Diện tích toàn phần: Stp = 2πRh + 2πR2.
- Thể tích: V = πR2h.
Xem thêm
Công thức tính diện tích xung quanh và thể tích của hình trụ (2024) chính xác nhất
Câu 19:
09/11/2024Tính thể tích V của khối nón có bán kính đáy r=√3 và chiều cao h=4.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải:
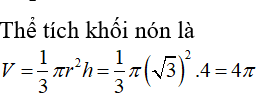
*Phương pháp giải:
Áp dụng công thức thể tích nón V=13S.h=13π.r2.h
*Lý thuyết:
- Định nghĩa hình chóp: Hình chóp là một hình có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này được gọi là đỉnh của chóp.
- Có 2 loại chóp phổ biến là chóp tam giác và chóp tứ giác
- Chú ý:
+ Đường cao của hình chóp là đường thẳng qua đỉnh và vuông góc với đáy.
+ Hình chóp có các cạnh bên bằng nhau thì chân đường cao là tâm đường tròn ngoại tiếp đa giác đáy.
+ Hình chóp có các mặt bên cùng tạo với đáy một góc bằng nhau thì chân đường cao là tâm đường tròn nội tiếp đa giác đáy
+ Hình chóp có một mặt bên vuông góc với đáy thì chân đường cao là chân đường vuông góc kẻ từ đỉnh xuống cạnh đáy của mặt bên đó.
+ 2 mặt bên cùng vuông góc với đáy thì giao tuyến của chúng vuông góc với đáy.
Xem thêm
Công thức tính thể tích khối chóp và cách giải các dạng bài tập (2024) chi tiết nhất
Câu 20:
23/07/2024Tính theo a thể tích của một khối trụ có bán kính đáy là a, chiều cao bằng 2a.
 Xem đáp án
Xem đáp án
Chọn A
Câu 21:
22/07/2024Một khối nón có bán kính đáy bằng 3 và góc ở đỉnh bằng 60o thì có thể tích bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn A
Câu 22:
22/10/2024Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng: C
* Các lý thuyết thêm về mặt trụ, mặt cầu và mặt nón:
1. Diện tích và thể tích hình trụ
Cho hình trụ có bán kính đáy R và chiều cao h.
- Diện tích xung quanh: Sxq = 2πRh.
- Diện tích toàn phần: Stp = 2πRh + 2πR2.
- Thể tích: V = πR2h.

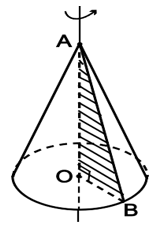
2. Diện tích và thể tích của hình nón
Đặt AC = l; l là đường sinh.
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
- Diện tích xung quanh: Sxq = πRl.
- Diện tích toàn phần: Stp = πRl + πR2.
- Thể tích: V=13πR2h.
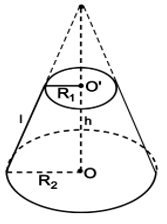
3. Diện tích và thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
- Diện tích xung quanh: Sxq = π (R + r) l.
- Thể tích: V=13πh(R2+Rr+r2).
Xem thêm các bài viết liên quan hay, chi tiết:
Bài toán về mặt cầu và phương pháp giải bài tập (có đáp án) – Toán 12
190 Bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải chi tiết
Câu 23:
21/07/2024Một tấm bìa hình tròn có bán kính bằng 5 được cắt thành hai hình quạt, sau đó quấn hai hình quạt đó thành hai hình nón (không có đáy). Biết một trong hai hình nón này có diện tích xung quanh là 15π. Tính thể tích hình nón còn lại. Giả sử chiều rộng các mép dán không đáng kể.
 Xem đáp án
Xem đáp án
Chọn A
Câu 24:
13/07/2024Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V1. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là V2. Tính tỉ số V1V2.
 Xem đáp án
Xem đáp án
Chọn C
Câu 25:
14/07/2024Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác đều có cạnh bằng a. Thể tích của khối nón là:
 Xem đáp án
Xem đáp án
Chọn D
Câu 27:
17/07/2024Cho hình trụ có bán kính đáy bằng R, chiều cao bằng h. Biết rằng hình trụ đó có diện tích toàn phần gấp ba diện tích xung quanh. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn A
Bài thi liên quan
-
Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học (P1) (Đề 1)
-
25 câu hỏi
-
40 phút
-
-
Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học (P1) (Đề 2)
-
25 câu hỏi
-
40 phút
-
