Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học
Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học (P1) (Đề 1)
-
688 lượt thi
-
25 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Gọi R,l,h lần lượt là bán kính đáy, độ dài đường sinh, chiều cao của hình nón (N). Diện tích xung quanh Sxq S của hình nón là
 Xem đáp án
Xem đáp án
Chọn D
Câu 2:
21/07/2024Một cái cốc hình trụ có bán kính đáy là 2cm , chiều cao 20cm . Trong cốc đang có một ít nước, khoảng cách giữa đáy cốc và mặt nước là 12cm (Hình vẽ). Một con quạ muốn uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6cm . Con quạ thông minh mổ những viên bi đá hình cầu có bán kính 0,6cm thả vào cốc nước để mực nước dâng lên. Để uống được nước thì con quạ cần thả vào cốc ít nhất bao nhiêu viên bi?
 Xem đáp án
Xem đáp án
Chọn B
Câu 3:
23/07/2024Một hình trụ có hai đáy là hai hình tròn (O;r) và (O’;r). Khoảng cách giữa hai đáy là OO' . Một hình nón có đỉnh O và có đáy là hình tròn (O’;r). Gọi S1 là diện tích xung quanh của hình trụ và S2 là diện tích xung quanh của hình nón. Tính tỉ số .
 Xem đáp án
Xem đáp án
Chọn D
.png)
Câu 4:
21/07/2024Cho hình nón có chiều cao bằng 8cm, bán kính đáy bằng 6cm. Diện tích toàn phần của hình nón đã cho bằng
 Xem đáp án
Xem đáp án
Chọn C
Câu 5:
21/07/2024Cho khối trụ có thể tích bằng ,chiều cao 5cm. Tính bán kính R của khối trụ đã cho
 Xem đáp án
Xem đáp án
Chọn A
Câu 6:
13/07/2024Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a. Diện tích xung quanh hình nón đó bằng:
 Xem đáp án
Xem đáp án
Chọn C
Câu 7:
22/07/2024Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Diện tích xung quanh hình trụ bằng:
 Xem đáp án
Xem đáp án
Chọn B
Câu 8:
14/07/2024Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 9:
16/07/2024Một hình trụ có bán kính đáy bằng chiều cao và bằng a. Một hình vuông ABCD có AB;CD là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng:
 Xem đáp án
Xem đáp án
Chọn D

Câu 10:
23/07/2024Cho tam giác ABC cân tại A, góc và AB = 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
 Xem đáp án
Xem đáp án
Chọn D
Câu 11:
16/07/2024Trải mặt xung quanh của một hình nón lên một mặt phẳng ta được hình quạt (xem hình bên dưới) là phần của hình tròn có bán kính bằng 3cm. Bán kính đáy r của hình nón ban đầu gần nhất với số nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn A
Câu 12:
22/07/2024Cho hình trụ có bán kính đáy R và độ dài đường sinh là l. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Chọn A
Câu 13:
22/07/2024Cho hình trụ có chiều cao bằng bán kính đáy và bằng 4cm. Điểm A nằm trên đường tròn tâm O, điểm B nằm trên đường tròn đáy tâm O' của hình trụ. Biết khoảng cách giữa 2 đường thẳng OO' và AB bằng cm. Khi đó khoảng cách giữa OA' và OB bằng:
 Xem đáp án
Xem đáp án
Chọn D
Câu 14:
22/07/2024Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng 60°. Thể tích của khối nón đã cho là
 Xem đáp án
Xem đáp án
Chọn A
Câu 15:
20/07/2024Người ta đổ một cái cống bằng cát, đá, xi măng và sắt thép như hình vẽ bên dưới. Thể tích nguyên vật liệu cần dùng là
 Xem đáp án
Xem đáp án
Chọn A
Câu 16:
23/07/2024Thể tích lớn nhất của khối trụ nội tiếp hình cầu có bán kính R bằng:
 Xem đáp án
Xem đáp án
Chọn A
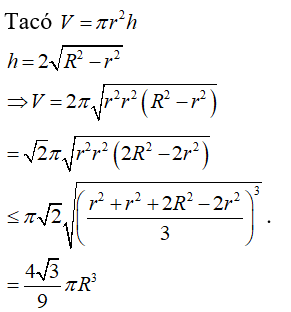
Câu 18:
20/07/2024Một bình đựng nước dạng hình nón (không có đáy), đừng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là .Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên).
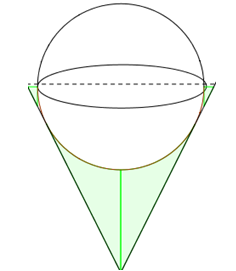
Thể tích V của nước còn lại trong bình bằng:
 Xem đáp án
Xem đáp án
Chọn B
Câu 19:
14/07/2024Nếu một hình nón có diện tích xung quanh gấp đôi diện tích của hình tròn đáy thì góc ở đỉnh của hình nón bằng:
 Xem đáp án
Xem đáp án
Chọn B
Câu 20:
28/11/2024Cho tam giác ABC vuông tại A. AB=c, AC=b. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải

*Phương pháp giải:

*Lý thuyết:
1.1. Nhận biết hình nón
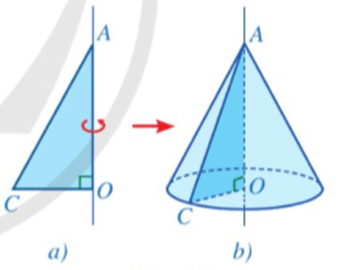
Cắt một miếng bìa có dạng tam giác vuông AOC. Khi quay miếng bìa một vòng quanh đường thẳng cố định chứa cạnh AO (Hình a), miếng bìa đó tạo nên một hình như ở Hình b.
Nhận xét: Hình được tạo ra khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác đó là hình nón.
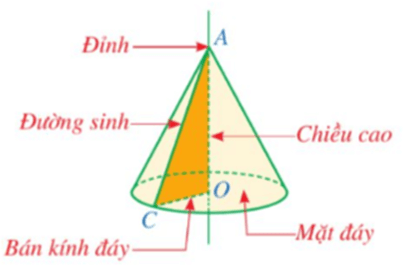
Với hình nón như ở hình vẽ trên, ta có:
⦁ Điểm A là đỉnh;
⦁ Hình tròn tâm O bán kính OC là mặt đáy;
⦁ Độ dài cạnh OC được gọi là bán kính đáy;
⦁ Độ dài cạnh AO được gọi là chiều cao;
⦁ Cạnh AC quét nên mặt xung quanh của hình nón, mỗi vị trí của cạnh AC được gọi là một đường sinh.
Chú ý: Nếu gọi độ dài đường sinh, chiều cao và bán kính đáy của hình nón lần lượt là l, h và r thì theo định lí Pythagore ta có: l2 = h2 + r2.
Xem thêm
Câu 21:
19/07/2024Một hình nón tròn xoay có độ dài đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng 9π. Khi đó đường cao của hình nón bằng:
 Xem đáp án
Xem đáp án
Chọn B
Câu 22:
17/11/2024Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt không thẳng hàng là:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải
*Phương pháp giải:
Tập hợp tâm các mặt cầu đi qua 3 điểm a b C phân biệt không thẳng hàng là trục của đường trong ngoại tiếp tam giác ABC
*Lý thuyết:
I. Mặt cầu và các khái niệm liên quan đến mặt cầu.
1. Mặt cầu
- Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O, bán kính r.
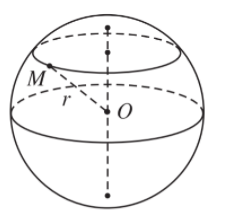
Ta kí hiệu mặt cầu tâm O, bán kính r là S(O; r) hay viết tắt là (S). Như vậy ta có mặt cầu S(O; r) = {M| OM = r}.
- Nếu hai điểm C; D nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.
- Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó, độ dài đường kính bằng 2r.
- Một mặt cầu được xác định nếu biết tâm và bán kính của nó hoặc biết một đường kính của mặt cầu đó.
Xem thêm
Câu 23:
17/07/2024Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ bằng 16π. Thể tích V của khối trụ bằng:
 Xem đáp án
Xem đáp án
Chọn D
Bài thi liên quan
-
Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học (P1) (Đề 2)
-
25 câu hỏi
-
40 phút
-
-
Bài tập mặt nón, mặt trụ, mặt cầu từ đề thi Đạị học (P1) (Đề 3)
-
29 câu hỏi
-
40 phút
-