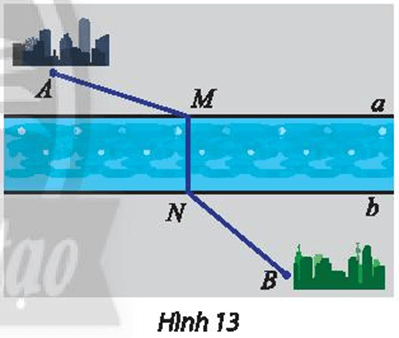
Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông

Lời giải Bài 6 trang 19 Chuyên đề Toán 11 sách Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

1 475 03/07/2023

Trang trước

Trang sau

Giải Chuyên đề Toán 11 Chân trời sáng tạo Bài 3: Phép đối xứng trục

Bài 6 trang 19 Chuyên đề Toán 11: Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.

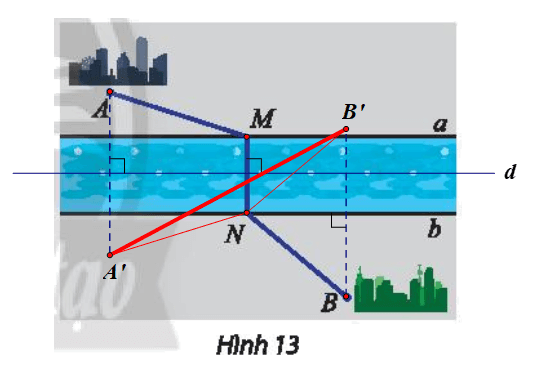
Bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Lời giải:

Bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Gọi d là đường trung trực của đoạn MN.

Suy ra điểm N là ảnh của điểm M qua Đ_d.

Lấy điểm A’ là ảnh của điểm A qua Đ_d.

Suy ra đoạn A’N là ảnh của đoạn AM qua Đ_d.

Do đó A’N = AM.

Lấy điểm B’ là ảnh của điểm B qua Đ_b.

Suy ra b là đường trung trực của đoạn BB’.

Mà N ∈ b (giả thiết).

Do đó NB’ = NB.

Ta có AM + NB = A’N + NB’.

Áp dụng bất đẳng thức tam giác cho ∆A’NB’, ta được: A’N + NB’ ≥ A’B’.

Do đó tổng khoảng cách AM + NB ngắn nhất khi và chỉ khi A’N + NB’ = A’B’.

Tức là, ba điểm A’, N, B’ thẳng hàng.

Vậy N là giao điểm của A’B’ và bờ b, M là điểm nằm bên bờ a thỏa mãn M = Đ_d(N), với d là đường trung trực của đoạn MN, A’ = Đ_d(A), B’ = Đ_b(B).

Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 14 Chuyên đề Toán 11: Trong các hình sau, hình nào có trục đối xứng?

Khám phá 1 trang 15 Chuyên đề Toán 11: Cho đường thẳng d. Gọi f là quy tắc xác định như sau:

Khám phá 2 trang 15 Chuyên đề Toán 11: Giả sử Đ_a là phép đối xứng trục qua đường thẳng a. Ta chọn hệ tọa độ Oxy...

Thực hành 1 trang 17 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x – y + 3 = 0 và đường tròn...

Vận dụng 1 trang 17 Chuyên đề Toán 11: Cho hai điểm A, B là vị trí của hai nhà máy nằm cùng một phía bờ sông là đường thẳng d

Khám phá 3 trang 17 Chuyên đề Toán 11: Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC...

Thực hành 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.

Vận dụng 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng trong các hình ở Hình 10.

Bài 1 trang 18 Chuyên đề Toán 11: Vẽ các hình sau đây vào giấy kẻ ô vuông và tìm ảnh của các hình đã cho qua phép đối xứng trục d.

Bài 2 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình x – y = 0...

Bài 3 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).

Bài 4 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)² + (y – 4)² = 25 và đường thẳng ∆: 2x + 3y + 4 = 0....

Bài 5 trang 19 Chuyên đề Toán 11: Cho tam giác ABC với B và C cố định. Vẽ hai đường tròn có tâm lần lượt là B, C...

Bài 6 trang 19 Chuyên đề Toán 11: Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông...

Bài 7 trang 19 Chuyên đề Toán 11: Vận dụng phép đối xứng trục để vẽ nhanh bình hoa theo hướng dẫn trong Hình 14.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

1 475 03/07/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: