Chuyên đề Toán 12 Bài 4 (Kết nối tri thức): Vận dụng đạo hàm để giải quyết một số bài toán tối ưu

Giải Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu

1. Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn

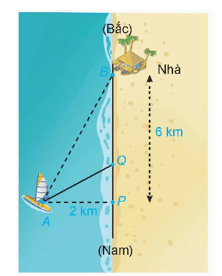
HĐ1 trang 35 Chuyên đề Toán 12: Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng đường còn lại để về nhà.

a) Hãy chọn các kí hiệu cho các đại lượng đã biết và đại lượng chưa biết trong bài toán trên.

b) Tìm các mối quan hệ giữa các kí hiệu trong câu a).

c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết bao nhiêu thời gian?

d) Nếu anh ấy chèo thuyền đến điểm Q, rồi đi bộ về nhà thì hết bao nhiêu thời gian?

Lời giải:

a) Kí hiệu v₁ là vận tốc chèo thuyền (v₁ = 3 km/h) và v₂ là vận tốc đi bộ (v₂ = 5 km/h).

Kí hiệu S₁ là quãng đường người đánh cá chèo thuyền và S₂ là quãng đường người đánh cá đi bộ dọc bờ biển.

b) Thời gian người đánh cá chèo thuyền là $t_1=\frac{S_1}{v_1}$ (giờ).

Thời gian người đó đi bộ là $t_2=\frac{S_2}{v_2}$ (giờ).

c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết

$T=t_1+t_2=\frac{S_1}{v_1}+\frac{S_2}{v_2}=\frac{2}{3}+\frac{6}{5}=\frac{28}{15}$ (giờ).

d) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết

$T=t_1+t_2=\frac{S_1}{v_1}+\frac{S_2}{v_2}=\frac{AQ}{3}+\frac{QB}{5}$ (giờ).

Xét ∆APQ vuông tại P, theo định lí Pythagore ta có:

AQ² = AP² + PQ² = 2² + PQ² = 4 + PQ².

Suy ra $AQ=\sqrt{4+P{Q}^2}\text{ (km).}$

Lại có QB = PB – PQ = 6 – PQ (km).

Vậy tổng thời gian để anh ấy chèo thuyền đến Q rồi đi bộ về nhà là:

$T=\frac{\sqrt{4+P{Q}^2}}{3}+\frac{6-PQ}{5}\text{ (km).}$

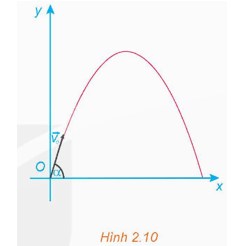
Luyện tập 1 trang 37 Chuyên đề Toán 12: Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v₀ = 9 m/s (H.2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình $y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+x\tan \alpha ,$ ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).

a) Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s²).

b) Xác định góc ném α để tầm ném xa của vật đạt giá trị lớn nhất.

Lời giải:

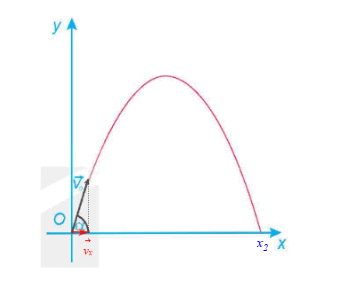
a) Ta luôn có y ≥ 0 và dễ thấy y = 0 tại x = x₁ = 0 và x = x₂ (hình vẽ).

Xét $y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+x\tan \alpha ,$ trên khoảng [0; x₂].

Đạo hàm của hàm y là $y^{\text{'}}=\frac{-g}{v_0^2{\cos }^2\alpha }x+\tan \alpha .$

Ta có $y^{\text{'}}=0\iff \frac{-g}{v_0^2{\cos }^2\alpha }x+\tan \alpha =0$

$\iff x=\tan \alpha \cdot \frac{v_0^2{\cos }^2\alpha }{g}$

$\iff x=\frac{v_0^2\sin \alpha \cdot \cos \alpha }{g}.$

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

$y\left(0\right)=0;y\left(\frac{v_0^2\sin \alpha \cos \alpha }{g}\right)=\frac{v_0^2{\sin }^2\alpha }{2g};y\left(x_2\right)=0.$

Vì giá trị $y\left(\frac{v_0^2\sin \alpha \cos \alpha }{g}\right)$ là giá trị lớn nhất trong ba giá trị trên, nên giá trị lớn nhất của y là $y=\frac{v_0^2{\sin }^2\alpha }{2g}\left(*\right),$ đạt được khi $x=\frac{v_0^2\sin \alpha \cos \alpha }{g}.$

Từ hình vẽ, ta có v_x = v₀.cosα, mà x = v_x.t nên $t=\frac{x}{v_x}=\frac{\frac{v_0^2\sin \alpha \cdot \cos \alpha }{g}}{v_0\cdot cos\alpha }=\frac{v_0\sin \alpha }{g}.\left(**\right)$

Thay v₀ = 9 m/s và g = 9,8 m/s² vào (*) và (**) ta được:

$y=\frac{9^2\cdot {\sin }^2\alpha }{2\cdot 9,8}=\frac{405{\sin }^2\alpha }{98},$ tại $t=\frac{9\sin \alpha }{9,8}=\frac{45\sin \alpha }{49}.$

Vậy vật đạt độ cao nhất trên quỹ đạo là $\frac{405{\sin }^2\alpha }{98}\text{ (m)}$ tại thời điểm $\frac{45\sin \alpha }{49}$ (s).

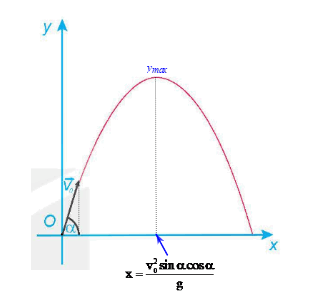
b) Từ câu a, ta có hình vẽ như sau:

Khi đó, tầm ném xa của vật là:

$L=\frac{2v_0^2\sin \alpha \cos \alpha }{g}=\frac{v_0^2\sin 2\alpha }{g}.$$x=\frac{v_0^2\sin \alpha \cos \alpha }{g}$

Xét hàm số $L=\frac{v_0^2\sin 2\alpha }{g}$ trên đoạn [0°; 90°].

Đạo hàm của hàm L là $L^{\text{'}}=\frac{2v_0^2\cos 2\alpha }{g}.$

Ta có $L^{\text{'}}=0\iff \frac{2v_0^2\cos 2\alpha }{g}=0\iff \cos 2\alpha =0\iff 2\alpha =90°\iff \alpha =45°.$

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

$L\left(0\right)=0;L\left(45°\right)=\frac{v_0^2}{g};L\left(90°\right)=0.$

Vì giá trị L(45°) là giá trị lớn nhất trong ba giá trị trên, nên giá trị nhỏ nhất của L đạt được khi α = 45°.

Vậy để tầm ném xa của vật đạt giá trị lớn nhất thì góc ném là 45°.

Luyện tập 2 trang 38 Chuyên đề Toán 12: (Định luật khúc xạ ánh sáng)

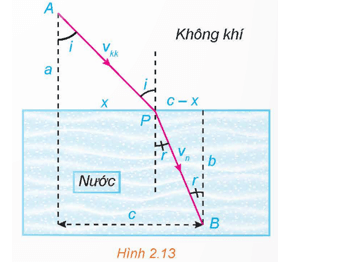
Gọi v_kk là vận tốc ánh sáng trong không khí và v_n là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A trong không khí đến một điểm B trong nước theo đường gấp khúc APB sao cho tổng thời gian di chuyển là nhỏ nhất (H.2.13). Vận dụng đạo hàm tìm cực trị của hàm số T(x) (tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB) để chứng tỏ rằng khi T(x) nhỏ nhất thì góc tới i và góc khúc xạ r thoả mãn phương trình $\frac{\sin i}{\sin r}=\frac{v_{kk}}{v_n}.$

Phương trình này được gọi là Định luật Snell.

Lời giải:

Từ hình vẽ, với 0 ≤ x ≤ c ta có: $AP=\sqrt{a^2+x^2}$ và $PB=\sqrt{b^2+{\left(c-x\right)}^2}.$

Thời gian ánh sáng di chuyển từ A đến P là: $t_1=\frac{AP}{v_{kk}}=\frac{\sqrt{a^2+x^2}}{v_{kk}}.$

Thời gian ánh sáng di chuyển từ P đến B là: $t_2=\frac{PB}{v_n}=\frac{\sqrt{b^2+{\left(c-x\right)}^2}}{v_n}.$

Khi đó, tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB là:

$T\left(x\right)=t_1+t_2=\frac{\sqrt{a^2+x^2}}{v_{kk}}+\frac{\sqrt{b^2+{\left(c-x\right)}^2}}{v_n}.$

Xét hàm số $T\left(x\right)=\frac{\sqrt{a^2+x^2}}{v_{kk}}+\frac{\sqrt{b^2+{\left(c-x\right)}^2}}{v_n}$ trên đoạn [0; c].

Đạo hàm của hàm T(x) là: $T^{\text{'}}\left(x\right)=\frac{x}{v_{kk}\sqrt{a^2+x^2}}-\frac{c-x}{v_n\sqrt{b^2+{\left(c-x\right)}^2}}.$

Ta có $T^{\text{'}}\left(x\right)=0\iff \frac{x}{v_{kk}\sqrt{a^2+x^2}}-\frac{c-x}{v_n\sqrt{b^2+{\left(c-x\right)}^2}}=0$

$\iff \frac{1}{v_{kk}}\cdot \frac{x}{\sqrt{a^2+x^2}}=\frac{1}{v_n}\cdot \frac{c-x}{\sqrt{b^2+{\left(c-x\right)}^2}}$

$\iff \frac{1}{v_{kk}}\cdot \sin i=\frac{1}{v_n}\cdot \sin r\iff \frac{\sin i}{\sin r}=\frac{v_{kk}}{v_n}.$

Giả sử x = x₀ thỏa mãn $\frac{\sin i}{\sin r}=\frac{v_{kk}}{v_n}.$

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

$$\begin{gathered} T\left(0\right)=\frac{a}{v_{kk}}+\frac{\sqrt{b^2+c^2}}{v_n}; \\ T\left(x_0\right)=\frac{\sqrt{a^2+x_0^2}}{v_{kk}}+\frac{\sqrt{b^2+{\left(c-x_0\right)}^2}}{v_n}; \\ T\left(c\right)=\frac{\sqrt{a^2+c^2}}{v_{kk}}+\frac{b}{v_n}. \end{gathered}$$

Ta có T(x₀) là giá trị nhỏ nhất trong các giá trị T(0), T(x₀), T(c).

Vậy T(x) nhỏ nhất khi góc tới i và góc khúc xạ r thỏa mãn phương trình $\frac{\sin i}{\sin r}=\frac{v_{kk}}{v_n}.$

2. Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong kinh tế

Luyện tập 3 trang 40 Chuyên đề Toán 12: Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là 27 triệu đồng/chiếc và giá bán ra là 31 triệu đồng/chiếc. Với giá bán này thì số lượng xe bán ra mối năm là 600 chiếc. Nhằm tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán. Ước tính rằng cứ giảm 1 triệu đồng/chiếc thi số lượng xe bán ra trong một năm tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để thu được lợi nhuận cao nhất?

Lời giải:

Gọi x (triệu đồng) là số tiền giảm cho mỗi chiếc xe, 0 ≤ x ≤ 31.

Số lượng chiếc xe bán được là: 600 + 200x (chiếc).

Hàm chi phí cho 600 + 200x chiếc xe là: (600 + 200x).27 (triệu đồng).

Hàm doanh thu cho 600 + 200x chiếc xe là:

(600 + 200x).(31 – x) (triệu đồng).

Khi đó, lợi nhuận thu được là:

P(x) = (600 + 200x).(31 – x) – (600 + 200x).27

= (600 + 200x)(4 – x) = 2 400 + 200x – 200x² (triệu đồng).

Để tối đa hóa lợi nhuận, thì ta phải tìm giá trị lớn nhất của hàm P(x) với 0 ≤ x ≤ 31.

Ta có P’(x) = 200 – 400x = 0 khi x = 0,5.

Khi đó P(0,5) = 2 450 (triệu đồng) là giá trị lớn nhất của hàm lợi nhuận, đạt được khi x = 0,5. Tức là mỗi chiếc xe nên giảm giá 0,5 triệu đồng.

Vậy doanh nghiệp nên định giá bán mới là 30,5 triệu đồng để thu được lợi nhuận cao nhất.

Luyện tập 4 trang 42 Chuyên đề Toán 12: Biết rằng C(x) = 16 000 + 500x – 1,64x² + 0,004x³ là hàm chi phí và p(x) = 1 700 – 7x là hàm cầu của x đơn vị hàng hóa. Hãy tìm mức sản xuất để lợi nhuận là lớn nhất.

Lời giải:

Hàm lợi nhuận là:

P(x) = xp(x) – C(x)

= x.(1 700 – 7x) – (16 000 + 500x – 1,64x² + 0,004x³)

= 1 700x – 7x² – 16 000 – 500x + 1,64x² – 0,004x³

= – 0,004x³ – 5,36x² + 1 200x – 16 000.

Ta cần tìm x để P(x) là lớn nhất.

Ta có P’(x) = – 0,012x² – 10,72x + 1 200.

P’(x) = 0 ⇔ – 0,012x² – 10,72x + 1 200 = 0

⇔ x ≈ 100,6.

Ta có P(100) = 46 400 và P(101) = 46 401,436 nên P(100) < P(101).

Do số đơn vị hàng hóa phải là số nguyên dương nên để lợi nhuận lớn nhất thì mức sản xuất là x = 100 đơn vị hàng hóa.

Bài tập

Bài 2.6 trang 42 Chuyên đề Toán 12: Một cửa sổ có dạng phía dưới là hình chữ nhật, phía trên là nửa hình tròn có đường kính bằng chiều rộng của hình chữ nhật (H.2.17). Biết độ dài mép ngoài của cửa sổ phần sát tường (kể cả phần nửa đường tròn phía trên) là 10 m. Hãy tính các kích thước của hình chữ nhật để cửa sổ có diện tích lớn nhất (kết quả làm tròn đến chữ số thập phân thứ hai).

Lời giải:

Gọi x (m) là chiều rộng của hình chữ nhật, 0 < x < 10.

Khi đó, bán kính của phần cửa sổ nửa hình tròn là $\frac{x}{2}$ (m).

Diện tích của phần cửa sổ nửa hình tròn là: $S_1=\frac{1}{2}\cdot \pi \cdot {\left(\frac{x}{2}\right)}^2=\frac{\pi x^2}{8}{\text{ (m}}^2\text{).}$

Độ dài mép ngoài của phần cửa nửa đường tròn chính là nửa chu vi đường tròn và bằng: $\pi \cdot \frac{x}{2}=\frac{\pi x}{2}\text{ (m).}$

Độ dài mép ngoài của phần cửa hình chữ nhật và cũng là chu vi hình chữ nhật, bằng: $10-\frac{\pi x}{2}\text{ (m).}$

Chiều dài của phần cửa sổ hình chữ nhật là $10-\frac{\pi x}{2}-=\frac{x}{2}=\text{10}-\frac{\left(\pi +1\right)x}{2}\text{ (m).}$

Diện tích của phần cửa sổ hình chữ nhật là:

$S_2=x\cdot \left[\text{10}-\frac{\left(\pi +1\right)x}{2}\right]=10x-\frac{\left(\pi +1\right)x^2}{2}{\text{ (m}}^2\text{).}$

Diện tích của cửa sổ là:

$S\left(x\right)=S_1+S_2=\frac{\pi x^2}{8}+10x-\frac{\left(\pi +1\right)x^2}{2}=10x-\frac{\left(3\pi +4\right)x^2}{8}{\text{ (m}}^2\text{).}$

Xét hàm $S\left(x\right)=10x-\frac{\left(3\pi +4\right)x^2}{8}$ trên khoảng (0; 10).

Ta có

$S^{\text{'}}\left(x\right)=10-\frac{\left(3\pi +4\right)x}{4},$$S^{\text{'}}\left(x\right)=0\iff 10-\frac{\left(3\pi +4\right)x}{4}=0\iff x=\frac{40}{3\pi +4}.$

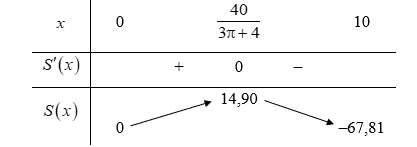
Lập bảng biến thiên của hàm số trên khoảng (0; 10):

Từ bảng biến thiên, ta có $\underset{\left(0;10\right)}{\max }S\left(x\right)\approx 14,90$ khi $x=\frac{40}{3\pi +4}\approx 2,98\text{ (m).}$

Vậy các kích thước của hình chữ nhật lần lượt là khoảng 2,98 m và $\text{10}-\frac{\left(\pi +1\right)\cdot 2,98}{2}\approx 3,83\text{ (m).}$

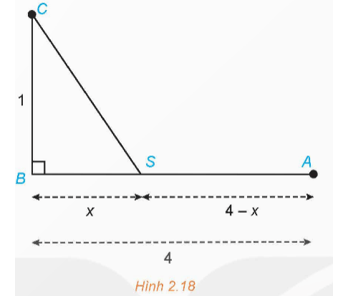
Bài 2.7 trang 42 Chuyên đề Toán 12: Người ta muốn kéo một đường dây điện từ nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây điện nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C (H. 2.18). Tìm vị trí của điểm S sao cho chi phí kéo đường dây điện là nhỏ nhất.

Lời giải:

Gọi x (km) là khoảng cách từ điểm B đến vị trí S, 0 ≤ x ≤ 4.

Từ hình vẽ ta có: AS = 4 – x (km) và $SC=\sqrt{1+x^2}$ (km).

Chi phí kéo đường dây điện từ A đến S (đặt ngầm dưới đất) là: 3 000(4 – x) (USD).

Chi phí kéo đường dây điện từ S đến C (đặt ngầm dưới nước) là:$5000\sqrt{1+x^2}$ (USD).

Khi đó, tổng chi phí kéo đường dây điện từ A đến C là:

$C\left(x\right)=3000\left(4–x\right)+5000\sqrt{1+x^2}$

$=12000-3000x+5000\sqrt{1+x^2}\left(\text{US}D\right).$

Ta cần tìm x để C(x) đạt giá trị nhỏ nhất.

Ta có $C^{\text{'}}\left(x\right)=-3000+5000\cdot \frac{x}{\sqrt{1+x^2}}.$

$C^{\text{'}}\left(x\right)=0\iff -3000+5000\cdot \frac{x}{\sqrt{1+x^2}}=0\iff \frac{x}{\sqrt{1+x^2}}=\frac{3}{5}$

$\iff 5x=3\sqrt{1+x^2}$

Từ giả thiết x ≥ 0 ta suy ra 25x² = 3(1 + x²), hay 22x² = 3, do đó $x=\sqrt{\frac{3}{22}}=\frac{\sqrt{66}}{22}.$

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

$C\left(0\right)=17000;C\left(\frac{\sqrt{66}}{22}\right)\approx 16222,20;C\left(4\right)\approx 20615,53.$

Vì giá trị $C\left(\frac{\sqrt{66}}{22}\right)$ là giá trị nhỏ nhất trong ba giá trị trên, nên giá trị nhỏ nhất của C(x) đạt được khi $x=\frac{\sqrt{66}}{22}\approx 0,369\text{ (km)}=369\text{ (m).}$

Vậy vị trí của điểm S cách B một khoảng 369 mét thì chi phí kéo đường dây điện là nhỏ nhất.

Bài 2.8 trang 43 Chuyên đề Toán 12: Một xe khách tuyến có sức chứa tối đa là 60 hành khách. Nếu chuyến xe chở x hành khách thì giá cho mỗi hành khách là $50000{\left(3-\frac{x}{40}\right)}^2$ (đồng). Xe có doanh thu cao nhất khi chở bao nhiêu hành khách, và doanh thu đó bằng bao nhiêu?

Lời giải:

Hàm doanh thu khi chở x khách hàng là:

$R\left(x\right)=50000{\left(3-\frac{x}{40}\right)}^2\cdot x$

$=50000x\left(9-\frac{3}{20}x+\frac{x^2}{1600}\right)$

= 450 000x – 7 500x² + 31,25x³ (đồng) với 0 ≤ x ≤ 60.

Đạo hàm của hàm R(x) là: R’(x) = 450 000 – 15 000x + 93,75x².

R’(x) = 0 ⇔ 450 000 – 15 000x + 93,75x² = 0

⇔ x = 120 (không thuộc [0; 60]) hoặc x = 40 (thỏa mãn).

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

R(0) = 0; R(40) = 8 000 000; R(60) = 6 750 000.

Vì giá trị R(40) là giá trị lớn nhất trong ba giá trị trên, nên giá trị lớn nhất của R(x) đạt được khi x = 40.

Vậy xe có doanh thu cao nhất khi chở 40 hành khách và doanh thu đó bằng 8 000 000 đồng.

Bài 2.9 trang 43 Chuyên đề Toán 12: Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích 5 ℓ. Giá sản xuất mặt xung quanh là 100 nghìn đồng m², giá sản xuất mặt đáy là 120 nghìn đồng/m². Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn? (Giả sử chi phí cho các mối nối không đáng kể)

Lời giải:

Đổi 5 ℓ = 5 dm³ = 0,005 m³.

Gọi x (m) là bán kính của đáy thùng đựng sơn hình trụ, x > 0.

Khi đó, chiều cao của thùng đựng sơn hình trụ là: $\frac{0,005}{\pi x^2}\text{ (m).}$

Diện tích xung quanh của thùng đựng sơn hình trụ là: $S_{xq}=2\pi x\cdot \frac{0,005}{\pi x^2}=\frac{\text{0,01}}{x}{\text{ (m}}^2\text{).}$

Diện tích đáy của thùng đựng sơn hình trụ là: S_đáy = πx² (m²).

Giá sản xuất mặt xung quanh của một thùng đựng sơn là: $100\cdot \frac{\text{0,01}}{x}=\frac{1}{x}$ (nghìn đồng).

Giá sản xuất hai mặt đáy của một thùng đựng sơn là: 120.2πx² = 240πx² (nghìn đồng).

Chi phí sản xuất một thùng sơn là: $C\left(x\right)=\frac{1}{x}+240\pi x^2$ (nghìn đồng) với x > 0.

Ta có $C^{\text{'}}\left(x\right)=-\frac{1}{x^2}+480\pi x.$

$C^{\text{'}}\left(x\right)=0\iff -\frac{1}{x^2}+480\pi x=0\iff 480\pi x^3=1\iff x=\sqrt[3]{\frac{1}{480\pi }}.$

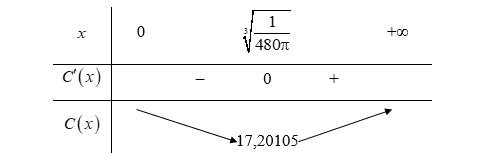
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).

Từ bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }C\left(x\right)\approx 17,20105$ khi $x=\sqrt[3]{\frac{1}{480\pi }}\approx 0,0872.$

Khi đó, chi phí thấp nhất để sản xuất một thùng sơn là khoảng 17,20105 nghìn đồng hay 17 201,05 đồng.

Ta có: 1 000 000 : 17 210,05 ≈ 58 135,98.

Vậy công ty có thể sản xuất được tối đa 58 135 thùng sơn.

Bài 2.10 trang 43 Chuyên đề Toán 12: Giả sử C(x) = 18 000 + 500x – 1,6x² + 0,004x³ (nghìn đồng) là hàm chi phí và p(x) = 1 500 – 3x (nghìn đồng) là hàm cầu của x đơn vị một loại hàng hoá nào đó.

a) Tìm công thức của hàm lợi nhuận P(x), biết rằng hàm lợi nhuận bằng hiệu của hàm doanh thu và hàm chi phí.

b) Tìm mức sản xuất x để lợi nhuận thu được là lớn nhất.

Lời giải:

a) Hàm doanh thu là: R(x) = x.p(x) = x.(1 500 – 3x) = 1 500x – 3x² (nghìn đồng).

Hàm lợi nhuận là:

P(x) = R(x) – C(x) = 1 500x – 3x² – (18 000 + 500x – 1,6x² + 0,004x³)

= 1 500x – 3x² – 18 000 – 500x + 1,6x² – 0,004x³

= – 0,004x³ – 1,4x² + 1 000x – 18 000.

Vậy công thức của hàm lợi nhuận là P(x) = – 0,004x³ – 1,4x² + 1 000x – 18 000 (nghìn đồng).

b) Xét hàm lợi nhuận P(x) = – 0,004x³ – 1,4x² + 1 000x – 18 000 (nghìn đồng) với x ≥ 0.

Ta có P’(x) = –0,012x² – 2,8x + 1 000.

P’(x) = 0 ⟺ –0,012x² – 2,8x + 1 000 = 0 ⇔ x ≈ 194,7.

Ta có P(194) = 94 104,064 và P(195) = 94 105,5 nên P(194) < P(105).

Do số đơn vị hàng hóa phải là số nguyên dương nên để lợi nhuận lớn nhất thì mức sản xuất là x = 195 đơn vị hàng hóa.