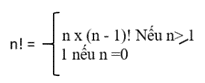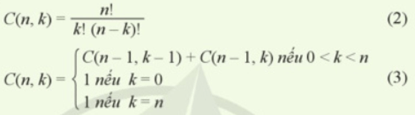Chuyên đề Tin học 11 Bài 1 (Cánh diều): Khái niệm đệ quy và ví dụ

Giải Chuyên đề Tin học 11 Bài 1: Khái niệm đệ quy và ví dụ

Khởi động trang 5 Chuyên đề Tin học 11: Trong toán học, n giai thừa (kí hiệu n!) là tích của n số nguyên dương đầu tiên n!=n x (n-1) x …x 1. Vậy ta có thể dùng công thức sau đây để tính n! được không?

Lời giải:

Ta có thể dùng công thức trên để tính m.

1. Một số ví dụ về đệ quy

Hoạt động 1 trang 6 Chuyên đề Tin học 11: Hai công thức sau đều được sử dụng để tính số cách chọn k phần tử từ n phần tử sau:

Theo em, trong hai công thức (2) và (3), công thức nào là công thức mang tính đệ quy? Em hãy giải thích cho lựa chọn của mình.

Lời giải:

Công thức 2 mang tính đệ quy

Sử dụng công thức ( 2 ) để tiếp tục quá trình tính toán, ta có F(n -1)- F(n - 2)+ F(n - 3), f( n - 2) = F(n - 3) + F(n - 4)... Do đó, nếu cứ gọi đến hàm F như vậy thÌ việc tính toán sẽ không có điểm dừng nên ta phải bỎ sang trường hợp đặc biệt được tính toán sẵn là hàm F tại n = 0 có giá trị 0 và tại n - 1 có giá trị 1. Công thức ( 2) là công thức mang tính đệ quy.

2. Khái niệm và các thành phần cơ bản trong định nghĩa đệ quy

Hoạt động 2 trang 7 Chuyên đề Tin học 11: Hàm đem Bupbe (búp bê A) ở Hình 3 được sử dụng để mô tả cách đếm số búp bê của bộ Matryoshka một cách đệ quy nếu búp bê A là búp bê lớn nhất của bộ. Em hãy cho biết dấu (?) trong hàm dem_Bupbe (búp bê A) cần được thay bằng gì.

Lời giải:

Dấu (?) trong hàm dem_Bupbe (búp bê A) cần được thay như sau:

return búp bê A

return dem_bupbe (con của búp bê A) + 1

Luyện tập 1 trang 8 Chuyên đề Tin học 11: Xét tập S được định nghĩa đệ quy như sau:

a) Phần cơ sở: 3 là phần tử của S.

b) Phần đệ quy: Nếu x thuộc S và y thuộc S thì x + y thuộc S (chú ý: x và y có thể có cùng giá trị).

Em hãy liệt kê 10 phần tử của tập S

Lời giải:

Liệt kê 10 phần tử của tập S như sau:

S = 0 ,1 ,1 ,2, 2, 3, 4, 5, 8, 13

Luyện tập 2 trang 8 Chuyên đề Tin học 11: Công thức toán học, dãy số hay hình ảnh nào sau đây được xây dựng mang tính đệ quy? Tại sao?

Lời giải:

Công thức toán học, dãy số hay hình ảnh được xây dựng mang tính đệ quy: a, d, g, l , m

=> Lời giải của nó có thể đưa về lời giải của bài toán P′ nhỏ hơn nó và có dạng giống nó, đồng thời lời giải của P′ không cần dùng tới P. Lời giải cho những bài toán như vậy được gọi là giải thuật đệ quy.

Luyện tập 3 trang 9 Chuyên đề Tin học 11: Kí hiệu tập hợp tất cả các số nguyên dương lẻ là S. Em hãy:

a) Đưa ra định nghĩa đệ quy cho tập S.

b) So sánh cách mô tả tập S sử dụng định nghĩa đệ quy mà em xây dựng được ở câu a) với hai cách sau đây:

Cách liệt kê các phân tử: S = {1, 3, 5, 7, 9....}

Cách sử dụng mệnh để logic: S = {x | x ∈ N*, x không chia hết cho 2}.

Lời giải:

a) Đệ quy là phương pháp dùng hàm để gọi lại chính nó. Trong quá trình giải thuật, một hàm ta lại có thể gọi lại chính tên hàm đó để tiếp tục giải dựa trên dữ liệu đã khai báo trước đó thì được gọi là đệ quy.

b) So sánh cách mô tả tập S

Ưu điểm lớn nhất của phép đệ quy là tiếp cận xử lý vấn đề bằng những đoạn code sạch, gọn gàng, dễ đọc, dễ hiểu. Nhược điểm rõ ràng là nguy cơ cao tràn bộ nhớ Stack như đã giải thích ở trên.

Cùng giải quyết một bài toán nhưng một phương án khác để thay thế đệ quy là sử dụng vòng lặp.

Dù vòng lặp có một ưu điểm là chỉ có một vòng duy nhất được gọi ra và ta sẽ không phải lo nghĩ gì về vấn đề tràn bộ nhớ Stack. Nhưng vòng lặp cũng có một nhược điểm so với đệ quy là code xử lý sẽ viết dài và phức tạp hơn.

Vận dụng trang 9 Chuyên đề Tin học 11: Trong phòng họp có người, mỗi người bắt tay lần lượt n - 1 người còn lại, giữa hai người bất kì chỉ bắt tay nhau đúng một lần. Em hãy:

a) Xác định số lượng cái bắt tay diễn ra trong phòng khi n = 0, 1, 2, 3, 4.

b) Đưa ra định nghĩa đệ quy cho hàm h(n) tính số lượng cái bắt tay đã diễn ra trong phòng có n người.

Gợi ý: Để xây dựng phân đệ quy cho h(n), em hãy xác định lời giải của bài toán khi có 0 người trong phòng từ lời giải của bài toán khi có n - 1 người trong phòng.

Lời giải:

Để xây dựng phân đệ quy cho h(n), em hãy xác định lời giải của bài toán khi có 0 người trong phòng từ lời giải của bài toán khi có n - 1 người trong phòng.

a) Trước hết ta nhận thấy rằng nếu có 2 người A và B bắt tay nhau tức là A đã bắt tay B và ngược lại B cũng bắt tay A.

Vì có 10 người nên mỗi người sẽ bắt tay với 10 – 1 = 9 người còn lại.

Tổng số lượt bắt tay của tất cả 10 người là: 10 x 9 = 90.

Do A bắt tay B thì B cũng bắt tay A nên số lần bắt tay ở trên đã được tính 2 lần.

=> Có 90 : 2 = 45 cái bắt tay.

b) Đệ quy là một phương pháp giải quyết vấn đề, trong đó nó sử dụng các trường hợp ví dụ đơn giản hơn của vấn đề để truy hồi, từ đó có thể giải quyết các vấn đề phức tạp hơn.

Câu hỏi tự kiểm tra trang 9 Chuyên đề Tin học 11: Trong những câu sau đây, câu nào đúng khi nói về đệ quy?

a) Ưu điểm của đệ quy là giúp cho mô tả đối tượng, sự việc trở nên ngắn gọn.

b) Khi đưa ra định nghĩa đệ quy của một đối tượng, không nhất thiết phải có phần cơ sở.

c) Trong một công thức đệ quy phần đệ quy đưa ra quy tắc xây dựng đối tượng mới chỉ từ một đối tượng cùng dạng có kích thước nhỏ hơn.

d) Trong một công thức đệ quy, phần cơ sở là phần chứa quy tắc đề xây dựng đối tượng mới từ một đối tượng cùng dạng có kích thước nhỏ hơn.

Lời giải:

Những câu sau đây đúng khi nói về đệ quy:

a) Ưu điểm của đệ quy là giúp cho mô tả đối tượng, sự việc trở nên ngắn gọn.

c) Trong một công thức đệ quy phần đệ quy đưa ra quy tắc xây dựng đối tượng mới chỉ từ một đôi tượng cùng dạng có kích thước nhỏ hơn.

d) Trong một công thức đệ quy, phần cơ sở là phần chứa quy tắc đề xây dựng đối tượng mới từ một đôi tượng cùng dạng có kích thước nhỏ hơn.

Xem thêm giải bài tập Chuyên đề Tin học 11 Cánh diều hay, chi tiết khác:

Bài 2: Tạo đoạn phim hoạt hình

Bài 3: Chỉnh sửa phim

Bài 4: Thực hành tổng hợp tạo phim hoạt hình

Bài 2: Khái niệm đệ quy và ví dụ

Bài 3: Thực hành thiết kế thuật toán đệ quy