Chứng minh rằng đường kính đi qua điểm chính giữa của một cung
Với giải bài tập 14 trang 72 sgk Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:
Giải Toán 9 Bài 2: Liên hệ giữa cung và dây
Video Giải Bài tập 14 trang 72 Toán lớp 9 Tập 2
Bài tập 14 trang 72 SGK Toán lớp 9 Tập 2:
a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.
b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Lời giải:
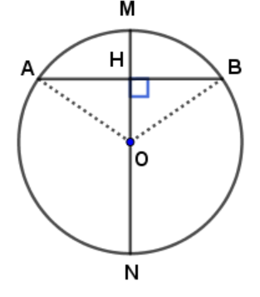
a)
Mệnh đề: Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
Chứng minh:
Gọi M là điểm chính giữa của cung nhỏ AB và MN là đường kính.
Do M là điểm chính giữa của cung nhỏ AB nên ta có:
Mà dây MA chắn cung nhỏ AM, dây MB chắn cung nhỏ MB
MA = MB (1)
Ta lại có: OA = OB (2) (cùng bằng bán kính đường tròn tâm O)
Từ (1) và (2) ta suy ra OM là đường trung trực của AB
Hay MN là đường trung trực của AB
Do đó , MN đi qua trung điểm của AB (đcpcm)
Mệnh đề đảo: Đường kính đi qua trung điểm của dây thì đi qua điểm chính giữa của cung căng dây đó.
Chứng minh:
Giả sử đường kính MN đi qua trung điểm H của dây AB
Xét tam giác OAB có:
OA = OB (cùng bằng bán kính đường tròn tâm O)
Do đó, tam giác OAB cân tại O
Có: H là trung điểm của AB
Do đó, OH là đường trung tuyến và cũng là đường phân giác của góc AOB
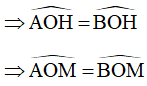
Mà ta có:
Góc AOM chắn cung nhỏ AM
Góc BOM chắn cung nhỏ BM
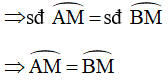
Do đó, M là điểm chính giữa của cung nhỏ AB (đcpcm)
Điều này chỉ đúng khi dây AB không đi qua O
Vậy phải thêm điều kiện để mệnh đề đảo đúng là: Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm chính giữa của cung căng dây đó.
b)
Mệnh đề: Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy.
Giả sử đường kính MN đi qua M là điểm chính giữa cung AB
Vì M là điểm chính giữa cung AB nên ta có:
Mà dây MA chắn cung nhỏ AM, dây MB chắn cung nhỏ MB
MA = MB (1)
Ta lại có: OA = OB (2) (cùng bằng bán kính đường tròn tâm O)
Từ (1) và (2) ta suy ra OM là đường trung trực của AB
Hay MN là đường trung trực của AB
(đcpcm)
Mệnh đề đảo: Đường kính vuông góc với dây cung thì đi qua điểm chính giữa của cung ấy.
Chứng minh:
Giả sử đường kính MN vuông góc với dây AB tại H
Xét tam giác OAB có:
OA = OB (cùng bằng bán kính đường tròn tâm O)
Do đó, tam giác OAB cân tại O
Có: OH vuông góc với AB tại H (do MN vuông góc với dây AB tại H)
Do đó, OH là đường cao và cũng là đường phân giác
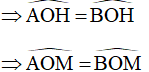
Mà ta có:
Góc AOM chắn cung nhỏ AM
Góc BOM chắn cung nhỏ BM
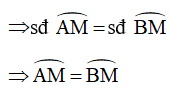
Do đó, M là điểm chính giữa của cung nhỏ AB (đcpcm)
*Phương pháp giải:
Sử dụng định lí để chứng minh
*Lý thuyết:
1. Định lí 1
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Hai cung bằng nhau căng hai dây bằng nhau.
- Hai dây bằng nhau căng hai cung bằng nhau.
Ví dụ 1. Cho đường tròn (O) như hình vẽ.
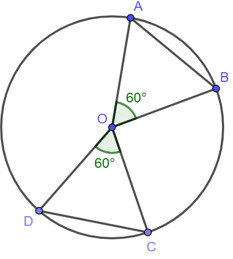
Trong hình vẽ (![]() ) nên AB = CD.
) nên AB = CD.
2. Định lí 2
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Cung lớn hơn căng dây lớn hơn.
- Dây lớn hơn căng cung lớn hơn.
Ví dụ 2. Cho đường tròn (I) như hình vẽ.
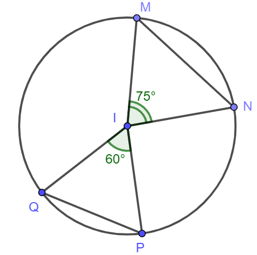
Trong hình vẽ :
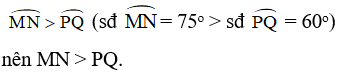
3. Bổ sung
Trong một đường tròn:
- Hai cung bị chắn giữa hai dây song song thì bằng nhau.
- Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
- Đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
- Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Xem thêm
Lý thuyết Liên hệ giữa cung và dây (mới 2024 + Bài Tập) - Toán 9
Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:
Câu hỏi 1 trang 71 Toán 9 Tập 2: Hãy chứng minh định lí:..
Câu hỏi 2 trang 71 Toán 9 Tập 2: Xem hình 11. Hãy viết giả thiết...
Bài tập 10 trang 71 Toán 9 Tập 2: a) Vẽ đường tròn tâm O, bán kính R = 2cm...
Bài tập 11 trang 72 Toán 9 Tập 2: Cho hai đường tròn bằng nhau...
Bài tập 12 trang 72 Toán 9 Tập 2: Cho tam giác ABC. Trên tia đối của tia AB...
Bài tập 13 trang 72 Toán 9 Tập 2: Chứng minh rằng trong một đường...
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9
