Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D
Với giải Bài 34 trang 71 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Luyện tập trang 70, 71
Video giải Bài 34 trang 71 Toán lớp 7 Tập 2
Bài 34 trang 71 Toán lớp 7 Tập 2: Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
a) BC = AD;
b) IA = IC, IB = ID;
c) Tia OI là tia phân giác của góc xOy.
*Phương pháp giải:
- Vẽ hình cho bài toán
- Viết giả thiết, kết luận cho bài toán
- Để chứng minh các cạnh bằng nhau ta sẽ đưa vào tam giác chứa các cạnh cần chứng minh để xét 2 tam giác đó bằng nhau theo các TH bằng nhau của tam giác
- Để chứng minh tia phân giác ta chỉ việc chỉ ra tia đó chia góc của nó thành 2 góc nhỏ bằng nhau
*Lời giải:
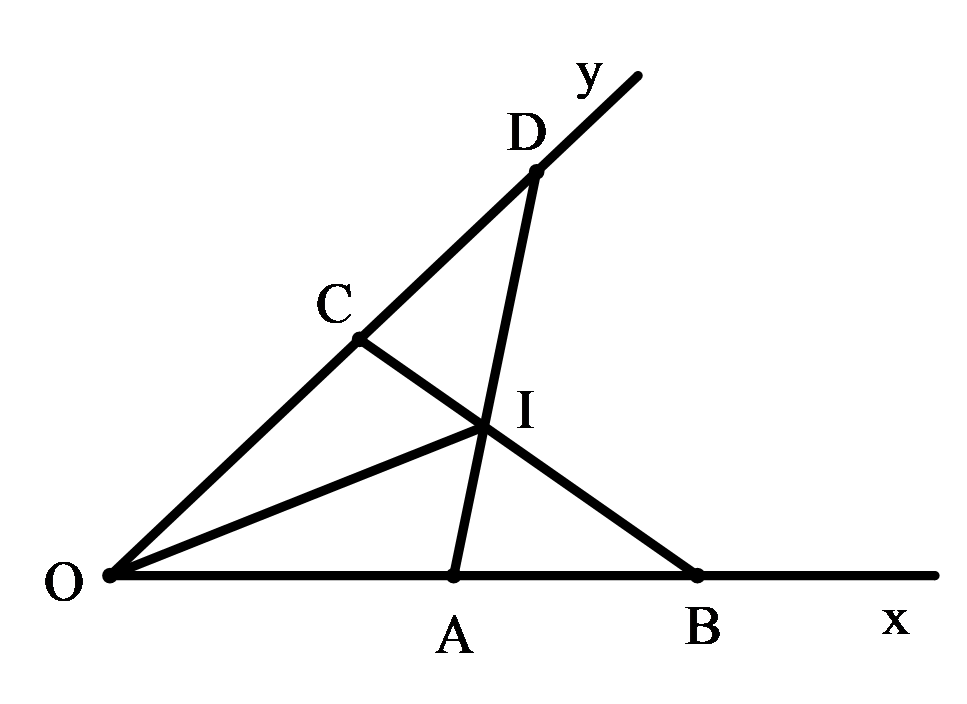
a) Xét ΔAOD và ΔCOB ta có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
Do đó ΔAOD = ΔCOB (c.g.c)
Suy ra AD = BC (hai cạnh tương ứng).
b) Vì ΔAOD = ΔCOB (theo câu a)
Suy ra (các góc tương ứng) (1)
Mà
(2)
Từ (1) và (2) suy ra .
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
Xét ΔDIC và ΔBIA ta có:
CD = AB (chứng minh trên)
Do đó ΔDIC = ΔBIA (g.c.g)
Suy ra IC = IA; ID = IB (các cặp cạnh tương ứng)
c) Xét ΔOIA và ΔOIC ta có:
OI là cạnh chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
Suy ra (hai góc tương ứng).
Suy ra OI là tia phân giác của góc xOy.
*Lý thuyết nắm thêm về sự đồng quy các đường trong tam giác:
a) Sự đồng quy của ba đường trung tuyến
* Định lí 1:Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mổi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
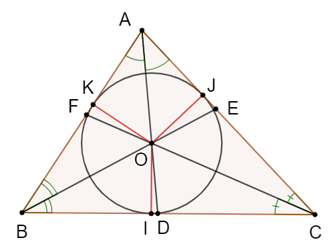
b) Sự đồng quy của ba đường phân giác
Định lí 2: Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Ví dụ: Trong tam giác ABC có các đường phân giác AD, BE, CF đồng quy tại điểm O.
Ta có: OI = OJ = OK.
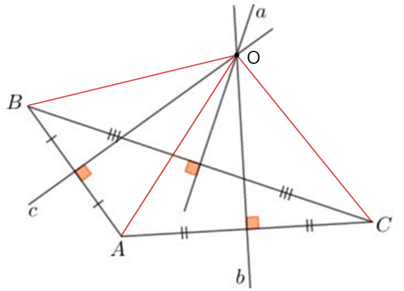
c) Sự đồng quy của ba đường trung trực
Định lí 1: Ba đường trung trực của một tam giác đồng quy tại một điểm. Điểm này cách đều ba đỉnh của tam giác.
Ví dụ: Trong tam giác ABC có các đường trung trực a, b, c đồng quy tại điểm O.
Khi đó: OA = OB = OC.
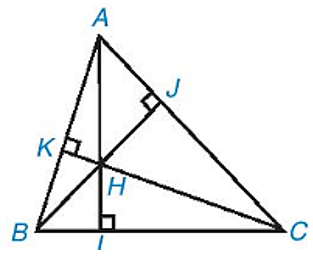
b) Sự đồng quy của ba đường cao
Định lí 2: Ba đường cao của một tam giác đồng quy tại một điểm.
Ví dụ: Trong tam giác ABC có các đường cao AI, BJ, CK đồng quy tại điểm H.
Chú ý:
- Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó.
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Tính chất ba đường phân giác của tam giác có đáp án
Trắc nghiệm Hai tam giác bằng nhau có đáp án - Toán lớp 7
Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác có đáp án
Xem thêm lời giải bài tập Toán lớp 7 chi tiết khác:
Bài 33 trang 70 Toán 7 Tập 2: Cho hai đường thẳng xx', yy' cắt nhau tại O (h. 33)...
Xem thêm các chương trình khác: