Câu hỏi:
14/12/2024 15,628
Xét tính chẵn lẻ của các hàm số sau:
a) y = sin 2x + tan 2x;
b) y = cos x + sin2 x;
c) y = sin x cos 2x;
d) y = sin x + cos x.
Xét tính chẵn lẻ của các hàm số sau:
a) y = sin 2x + tan 2x;
b) y = cos x + sin2 x;
c) y = sin x cos 2x;
d) y = sin x + cos x.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
a) Biểu thức sin 2x + tan 2x có nghĩa khi cos 2x ≠ 0 (do \(\tan 2x = \frac{{\sin 2x}}{{\cos 2x}}\)), tức là \(2x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\) \( \Leftrightarrow x \ne \frac{\pi }{4} + k\frac{\pi }{2},k \in \mathbb{Z}\).
Suy ra tập xác định của hàm số y = f(x) = sin 2x + tan 2x là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\frac{\pi }{2}|k \in \mathbb{Z}} \right\}\).
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– 2x) + tan (– 2x) = – sin 2x – tan 2x = – (sin 2x + tan 2x) = – f(x), ∀ x ∈ D.
Vậy y = sin 2x + tan 2x là hàm số lẻ.
b) Tập xác định của hàm số y = f(x) = cos x + sin2 x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cos (– x) + sin2 (– x) = cos x + (– sin x)2 = cos x + sin2 x = f(x), ∀ x ∈ D.
Vậy y = cos x + sin2 x là hàm số chẵn.
c) Tập xác định của hàm số y = f(x) = sin x cos 2x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) . cos (– 2x) = – sin x . cos 2x = – f(x), ∀ x ∈ D.
Vậy y = sin x cos 2x là hàm số lẻ.
d) Tập xác định của hàm số y = f(x) = sin x + cos x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) + cos (– x) = – sin x + cos x ≠ – f(x).
Vậy y = sin x + cos x là hàm số không chẵn, không lẻ.
*Phương pháp giải:
Bước 1: Tìm tập xác định D của hàm số, khi đó:
- Nếu D là tập đối xứng (tức là ), ta thực hiện tiếp bước 2.
- Nếu D không phải là tập đối xứng (tức là mà ), ta kết luận hàm số không chẵn cũng không lẻ.
Bước 2: Xác định f(-x), khi đó:
- Nếu f(-x) = f(x) kết luận hàm số là hàm chẵn.
- Nếu f(-x) = - f(x) kết luận hàm số là hàm lẻ.
- Ngoài ra kết luận hàm số không chẵn cũng không lẻ.
*Lý thuyết:
a) Tính chẵn, lẻ của hàm số:
* Định nghĩa:
- Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu: thì và f(-x) = f(x).
Đồ thị hàm số chẵn nhận trục tung Oy làm trục đối xứng.
- Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu: thì và f(-x) = - f(x).
Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.
* Đối với hàm số lượng giác:
- Hàm số y = sinx là hàm số lẻ trên D = R.
- Hàm số y = cosx là hàm số chẵn trên D = R.
- Hàm số y = tanx là hàm số lẻ trên .
- Hàm số y = cotx là hàm số lẻ trên .
b) Tính tuần hoàn và chu kì của hàm số:
* Định nghĩa:
- Hàm số y = f(x) xác định trên tập hợp D, được gọi là hàm số tuần hoàn nếu có số sao cho với mọi ta có ; và f(x + T) = f(x).
- Nếu có số dương T nhỏ nhất thỏa mãn các điều kiện trên thì T gọi là chu kì của hàm tuần hoàn f.
* Đối với hàm số lượng giác:
Hàm số y = sinx; y = cosx tuần hoàn với chu kì .
Hàm số y = tanx; y = cotx tuần hoàn với chu kì .
Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tập giá trị của các hàm số sau:
a) y = \(2\sin \left( {x - \frac{\pi }{4}} \right) - 1\);
b) y = \(\sqrt {1 + \cos x} - 2\).
Tìm tập giá trị của các hàm số sau:
a) y = \(2\sin \left( {x - \frac{\pi }{4}} \right) - 1\);
b) y = \(\sqrt {1 + \cos x} - 2\).
Câu 4:
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số h(t) = \(90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó h(t) là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm t giây.
a) Tìm chu kì của sóng.
b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số h(t) = \(90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó h(t) là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm t giây.
a) Tìm chu kì của sóng.
b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
Câu 5:
Cho hàm số y = cos x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cos x trên đoạn [– π; π] bằng cách tính giá trị của cos x với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của cos x với những x âm.
x
– π
\( - \frac{{3\pi }}{4}\)
\( - \frac{\pi }{2}\)
\( - \frac{\pi }{4}\)
0
\(\frac{\pi }{4}\)
\(\frac{\pi }{2}\)
\(\frac{{3\pi }}{4}\)
π
y = cos x
?
?
?
?
?
?
?
?
?
Bằng cách lấy nhiều điểm M(x; cos x) với x ∈ [– π; π] và nối lại ta được đồ thị hàm số y = cos x trên đoạn [– π; π].
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kì T = 2π, ta được đồ thị của hàm số y = cos x như hình dưới đây.
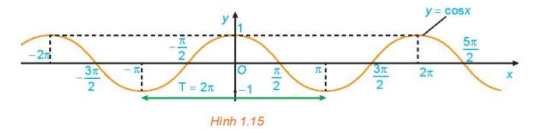
Từ đồ thị ở Hình 1.15, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số y = cos x.
Cho hàm số y = cos x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cos x trên đoạn [– π; π] bằng cách tính giá trị của cos x với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của cos x với những x âm.
|
x |
– π |
\( - \frac{{3\pi }}{4}\) |
\( - \frac{\pi }{2}\) |
\( - \frac{\pi }{4}\) |
0 |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{2}\) |
\(\frac{{3\pi }}{4}\) |
π |
|
y = cos x |
? |
? |
? |
? |
? |
? |
? |
? |
? |
Bằng cách lấy nhiều điểm M(x; cos x) với x ∈ [– π; π] và nối lại ta được đồ thị hàm số y = cos x trên đoạn [– π; π].
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kì T = 2π, ta được đồ thị của hàm số y = cos x như hình dưới đây.

Từ đồ thị ở Hình 1.15, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số y = cos x.
Câu 6:
Từ đồ thị của hàm số y = tan x, hãy tìm các giá trị x sao cho tan x = 0.
Câu 7:
Giả sử vận tốc v (tính bằng lít/giây) của luồng khí trong một chu kì hô hấp (tức là thời gian từ lúc bắt đầu của một nhịp thở đến khi bắt đầu của nhịp thở tiếp theo) của một người nào đó ở trạng thái nghỉ ngơi được cho bởi công thức
\(v = 0,85\sin \frac{{\pi t}}{3}\),
trong đó t là thời gian (tính bằng giây). Hãy tìm thời gian của một chu kì hô hấp đầy đủ và số chu kì hô hấp trong một phút của người đó.
Giả sử vận tốc v (tính bằng lít/giây) của luồng khí trong một chu kì hô hấp (tức là thời gian từ lúc bắt đầu của một nhịp thở đến khi bắt đầu của nhịp thở tiếp theo) của một người nào đó ở trạng thái nghỉ ngơi được cho bởi công thức
\(v = 0,85\sin \frac{{\pi t}}{3}\),
trong đó t là thời gian (tính bằng giây). Hãy tìm thời gian của một chu kì hô hấp đầy đủ và số chu kì hô hấp trong một phút của người đó.
Câu 8:
So sánh:
a) sin(x + 2π) và sin x;
b) cos(x + 2π) và cos x;
c) tan(x + π) và tan x;
d) cot(x + π) và cot x.
So sánh:
a) sin(x + 2π) và sin x;
b) cos(x + 2π) và cos x;
c) tan(x + π) và tan x;
d) cot(x + π) và cot x.
Câu 9:
Cho hàm số y = tan x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = tan x trên khoảng \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\).
x
\( - \frac{\pi }{3}\)
\( - \frac{\pi }{4}\)
\( - \frac{\pi }{6}\)
0
\(\frac{\pi }{6}\)
\(\frac{\pi }{4}\)
\(\frac{\pi }{3}\)
y = tan x
?
?
?
?
?
?
?
Bằng cách lấy nhiều điểm M(x; tan x) với x ∈ \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số y = tan x trên khoảng \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = tan x như hình dưới đây.
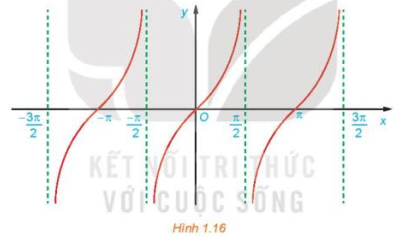
Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số y = tan x.
Cho hàm số y = tan x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = tan x trên khoảng \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\).
|
x |
\( - \frac{\pi }{3}\) |
\( - \frac{\pi }{4}\) |
\( - \frac{\pi }{6}\) |
0 |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
|
y = tan x |
? |
? |
? |
? |
? |
? |
? |
Bằng cách lấy nhiều điểm M(x; tan x) với x ∈ \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số y = tan x trên khoảng \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = tan x như hình dưới đây.

Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số y = tan x.
Câu 10:
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\,\frac{{3\pi }}{2}} \right]\) để hàm số y = tan x nhận giá trị âm.
Câu 12:
Hàm số hằng f(x) = c (c là hằng số) có phải hàm số tuần hoàn không? Nếu hàm số tuần hoàn thì nó có chu kì không?
Câu 13:
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};\,2\pi } \right]\) để hàm số y = cot x nhận giá trị dương.
Câu 14:
Trong Vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0), ωt + φ là pha của dao động tại thời điểm t và φ ∈ [–π; π] là pha ban đầu của dao động. Dao động điều hòa này có chu kì \(T = \frac{{2\pi }}{\omega }\) (tức là khoảng thời gian để vật thực hiện một dao động toàn phần).
Giả sử một vật dao động điều hòa theo phương trình x(t) = – 5cos 4πt (cm).
a) Hãy xác định biên độ và pha ban đầu của dao động.
b) Tính pha của dao động tại thời điểm t = 2 (giây). Hỏi trong khoảng thời gian 2 giây, vật thực hiện được bao nhiêu dao động toàn phần?
Trong Vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0), ωt + φ là pha của dao động tại thời điểm t và φ ∈ [–π; π] là pha ban đầu của dao động. Dao động điều hòa này có chu kì \(T = \frac{{2\pi }}{\omega }\) (tức là khoảng thời gian để vật thực hiện một dao động toàn phần).
Giả sử một vật dao động điều hòa theo phương trình x(t) = – 5cos 4πt (cm).
a) Hãy xác định biên độ và pha ban đầu của dao động.
b) Tính pha của dao động tại thời điểm t = 2 (giây). Hỏi trong khoảng thời gian 2 giây, vật thực hiện được bao nhiêu dao động toàn phần?
Câu 15:
Tìm tập xác định của các hàm số sau:
a) \(y = \frac{{1 - \cos x}}{{\sin x}}\);
b) \(y = \sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \).
Tìm tập xác định của các hàm số sau:
a) \(y = \frac{{1 - \cos x}}{{\sin x}}\);
b) \(y = \sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \).


