Câu hỏi:
17/07/2024 168Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng : và : . Khi hai mặt phẳng và tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng ?
A. .
B. .
C. .
D. .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Ta có ; .
Gọi là góc tạo bởi hai mặt phẳng và mặt phẳng .
Ta có ; ;
Để và tạo với nhau một góc nhỏ nhất thì lớn nhất nhỏ nhất.
Mà nên giá trị lớn nhất là khi .
Khi đó : .
Vậy .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Gọi là một nguyên hàm của hàm số , biết . Tính tổng các nghiệm của phương trình .
Câu 3:
Cho hàm số liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?
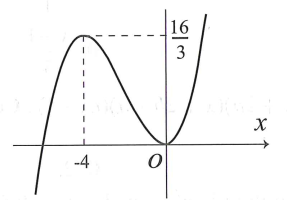
Câu 4:
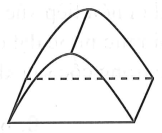
Để chuẩn bị cho hội trại do Đoàn trường tổ chức, lớp 12A dự định dựng một cái lều trại có hình parabol nhu hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 6 mét, đỉnh trại cách nền 3 mét. Tính thể tích phần không gian bên trong trại.
Câu 6:
Cho khối tứ diện đều ABCD cạnh bằng a. Gọi M, N là trung điểm các cạnh AB, BC và E là điểm thuộc tia đối DB sao cho . Biết rằng mặt phẳng chia khối tứ diện thành hai khối đa diện, trong đó khối đa diện chứa đỉnh B có thể tích là . Khẳng định nào sau đây là đúng?
Câu 7:
Cho một đa giác đều có 15 đỉnh. Người ta lập một tứ giác có 4 đỉnh là 4 đỉnh của . Tính số tứ giác được lập thành mà không có cạnh nào là cạnh của .
Câu 10:
Cho khối trụ có bán kính đáy bằng a và chiều cao bằng . Thể tích của khối trụ bằng
Câu 11:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng có phương trình là . Tính góc giữa và mặt phẳng .
Câu 12:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là
Câu 13:
Tìm tất cả các giá trị của tham số m để hàm số có hai điểm cực trị.
Câu 14:
Cho hàm số đa thức , . Đồ thị hàm số cắt trục hoành tại các điểm có hoành độ lần lượt là –1; ; ; . Số điểm cực trị của hàm số là
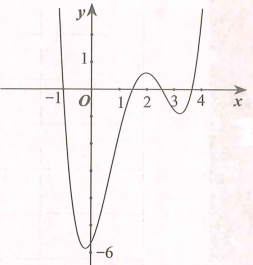
Câu 15:
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên dưới
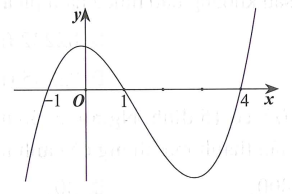
Bất phương trình nghiệm đúng với mọi khi và chỉ khi



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)