Câu hỏi:
18/07/2024 128
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(5; 0; 0) và B(3; 4; 0). Với C là điểm nằm trên trục Oz, gọi H là trực tâm của tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(5; 0; 0) và B(3; 4; 0). Với C là điểm nằm trên trục Oz, gọi H là trực tâm của tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A. √3
B. √32
C. √52
D. √54
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
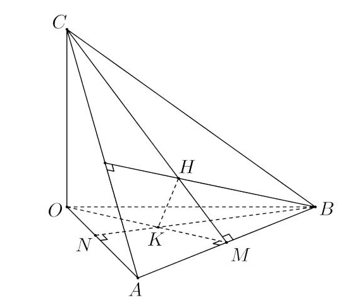
Ta có (OAB)=(Oxy),C∈Oz suy ra OC⊥(OAB).
Mà B(3;4;0)⇒OB=√32+42=5=OA⇒ΔOAB cân tại O.
Gọi M là trung điểm của AB, K là trực tâm của tam giác OAB
Suy ra OM⊥AB và K∈OM.
Ta có {AB⊥OMAB⊥OC⇒AB⊥(OCM)⇒AB⊥HK (do HK⊂(OCM)) (1).
Mặt khác {BK⊥OABK⊥OC⇒BK⊥(OAC)⇒BK⊥AC.
Mà BH⊥AC (do H là trực tâm của ΔABC) suy ra AC⊥(BHK)⇒AC⊥HK (2).
Từ (1) và (2) suy ra HK⊥(ABC)⇒HK⊥HM⇒ΔKHM vuông tại H.
Vì M, K (OCM) cố định và ^KHM=900 nên H thuộc đường tròn đường kính KM.
Gọi N là hình chiếu của B lên trục Ox suy ra N(3; 0; 0)
Từ đó ta tính được NA = 2, BN = 4 và AB=2√5.
Ta có ΔBMK đồng dạng ΔBNA (g.g) nên suy ra MKNA=BMBN⇔MK2=12AB4⇔MK=√52.
Vậy khi C di động trên trục Oz thì H luôn thuộc đường tròn cố định có bán kính bằng MK2=√54.
Chọn D.

Ta có (OAB)=(Oxy),C∈Oz suy ra OC⊥(OAB).
Mà B(3;4;0)⇒OB=√32+42=5=OA⇒ΔOAB cân tại O.
Gọi M là trung điểm của AB, K là trực tâm của tam giác OAB
Suy ra OM⊥AB và K∈OM.
Ta có {AB⊥OMAB⊥OC⇒AB⊥(OCM)⇒AB⊥HK (do HK⊂(OCM)) (1).
Mặt khác {BK⊥OABK⊥OC⇒BK⊥(OAC)⇒BK⊥AC.
Mà BH⊥AC (do H là trực tâm của ΔABC) suy ra AC⊥(BHK)⇒AC⊥HK (2).
Từ (1) và (2) suy ra HK⊥(ABC)⇒HK⊥HM⇒ΔKHM vuông tại H.
Vì M, K (OCM) cố định và ^KHM=900 nên H thuộc đường tròn đường kính KM.
Gọi N là hình chiếu của B lên trục Ox suy ra N(3; 0; 0)
Từ đó ta tính được NA = 2, BN = 4 và AB=2√5.
Ta có ΔBMK đồng dạng ΔBNA (g.g) nên suy ra MKNA=BMBN⇔MK2=12AB4⇔MK=√52.
Vậy khi C di động trên trục Oz thì H luôn thuộc đường tròn cố định có bán kính bằng MK2=√54.
Chọn D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cổng trường Đại học Bách Khoa Hà Nội có hình dạng Parabol, chiều rộng 8m, chiều cao 12,5m. Diện tích của cổng là:
Cổng trường Đại học Bách Khoa Hà Nội có hình dạng Parabol, chiều rộng 8m, chiều cao 12,5m. Diện tích của cổng là:
Câu 2:
Trong không gian Oxyz, cho điểm M(3; 2; -1). Hình chiếu vuông góc của điểm M lên trục Oz là điểm:
Trong không gian Oxyz, cho điểm M(3; 2; -1). Hình chiếu vuông góc của điểm M lên trục Oz là điểm:
Câu 5:
Trong không gian Oxyz, đường thẳng đi qua điểm A(1; 4; -7) và vuông góc với mặt phẳng x+2y−2z−3=0 có phương trình là
Trong không gian Oxyz, đường thẳng đi qua điểm A(1; 4; -7) và vuông góc với mặt phẳng x+2y−2z−3=0 có phương trình là
Câu 6:
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức.
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức.
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a,BC=a√3. Cạnh bên SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc 300. Tính thể tích V của khối chóp S.ABCD theo a.
Câu 8:
Cho bất phương trình: 1+log5(x2+1)≥log5(mx2+4x+m) (1). Tìm tất cả các giá trị của m để (1) được nghiệm đúng với mọi số thực x
Câu 13:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P):z−2x+3=0. Một vectơ pháp tuyến của (P) là:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P):z−2x+3=0. Một vectơ pháp tuyến của (P) là:
Câu 14:
Tổng bình phương các giá trị của tham số m để đường thẳng d:y=−x−m cắt đồ thị (C):y=x−2x−1 tại hai điểm phân biệt A, B với AB=√10 là
Tổng bình phương các giá trị của tham số m để đường thẳng d:y=−x−m cắt đồ thị (C):y=x−2x−1 tại hai điểm phân biệt A, B với AB=√10 là
Câu 15:
Cho f(x), g(x) là các hàm số xác định và liên tục trên ℝ. Trong các mệnh đề sau, mệnh đề nào sai?
Cho f(x), g(x) là các hàm số xác định và liên tục trên ℝ. Trong các mệnh đề sau, mệnh đề nào sai?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)