Trong không gian Oxyz, cho tam giác ABC có $A(1;0;0), B(0;0;1), C(2;1;1).$ Tam giác ABC có diện tích bằng

Đáp án đúng: C.

*Lời giải:

Diện tích tam giác ABC là

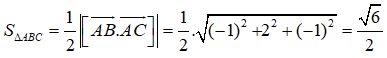
*Phương pháp giải:

- Tính: Độ dài của một vecto.

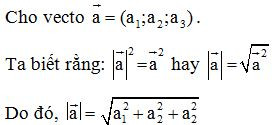
- Từ đó tính ra S tam giác 

*Lý thuyết cần nắm và các dạng bài toán về hệ tọa độ trong không gian:

1. Hệ tọa độ trong không gian

1.1. Tọa độ của điểm và của vecto

1.1.1. Hệ tọa độ

Trong không gian, xét ba trục tọa độ x’Ox; y’Oy; z’Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi $\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}$ lần lượt là các vectơ đơn vị, trên các trục x’Ox; y’Oy; z’Oz.

Hệ ba trục như vậy gọi là hệ trục tọa độ Đề- các vuông góc Oxyz trong không gian, hay đơn giản gọi là hệ trục tọa độ Oxyz.

Điểm O được gọi là gốc tọa độ.

Các mặt phẳng (Oxy); (Oyz); (Ozx) đôi một vuong góc với nhau được gọi là các mặt phẳng tọa độ.

Không gian với hệ tọa độ Oxyz còn gọi là không gian Oxyz.

- Vì $\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}$ là các vecto đơn vị đôi một vuông góc với nhau nên: ${\overrightarrow{i}}^2={\overrightarrow{j}}^2={\overrightarrow{k}}^2=1$ và $\overrightarrow{i}.\overrightarrow{j}=\overrightarrow{j}.\overrightarrow{k}=\overrightarrow{k}.\overrightarrow{i}=0$

1.1.2. Tọa độ của một điểm

- Trong không gian Oxyz, cho một điểm M tùy ý. Vì ba vecto $\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}$ không đồng phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho: $\overrightarrow{OM}=x.\overrightarrow{i}+y.\overrightarrow{j}+z.\overrightarrow{k}$

- Ngược lại, với bộ ba số (x; y; z) ta có một điểm M duy nhất trong không gian thỏa mãn hệ thức $\overrightarrow{OM}=x.\overrightarrow{i}+y.\overrightarrow{j}+z.\overrightarrow{k}$

 

- Ta gọi bộ ba số (x; y; z) là tọa độ của điểm M đối với hệ trục tọa độ Oxyz đã cho và viết: M = ( x; y; z) hoặc M (x; y; z).

1.1.3. Tọa độ của vecto

- Trong không gian Oxyz cho vecto $\overrightarrow{a}$, khi đó luôn tồn tại duy nhất bộ ba số (a1; a2; a3) sao cho $\overrightarrow{a}=a_1.\overrightarrow{i}+a_2.\overrightarrow{j}+a_3.\overrightarrow{k}$

Ta gọi bộ ba số (a1; a2 ; a3) là tọa độ của vecto $\overrightarrow{a}$ đối với hệ tọa độ Oxyz cho trước và viết $\overrightarrow{a}$(a1; a2 ; a3) hoặc $\overrightarrow{a}$(a1; a2 ; a3).

- Nhận xét : Trong hệ tọa độ Oxyz, tọa độ của điểm M chính là tọa độ của vecto $\overrightarrow{OM}$

Ta có: M(x; y; z)$\iff \overrightarrow{OM}(x;y;z)$

1.2. Biểu thức tọa độ của các phép toán của vecto

- Định lí: Trong không gian Oxyz, cho hai vecto

 

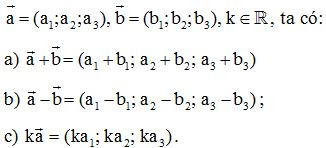
3. Biểu thức tọa độ của tích vô hướng.

- Định lí:

Trong không gian Oxyz, tích vô hướng của hai vecto $\overrightarrow{a}=(a_1;a_2;a_3),$$\overrightarrow{b}=(b_1;b_2;b_3)$ được xác định bởi công thức: $\overrightarrow{a}.\overrightarrow{b}=a_1.b_1+a_2.b_2+a_3.b_3$

4. Ứng dụng

a) Độ dài của một vecto.

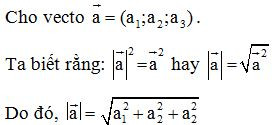
b) Khoảng cách giữa hai điểm.

Trong khong gian Oxyz, cho hai điểm A(xA ; yA ; zA) và B(xB; yB ; zB). Khi đó, khoảng cách giữa hai điểm A và B chính là độ dài của vecto $\overrightarrow{AB}$. Do đó, ta có:

c) Góc giữa hai vecto.

Nếu là góc góc giữa hai vecto $\overrightarrow{a}=(a_1;a_2;a_3)$ và $\overrightarrow{b}=(b_1;b_2;b_3)$ với $\overrightarrow{a};\overrightarrow{b}\ne \overrightarrow{0}$ thì

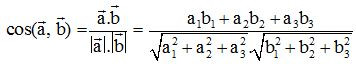
Từ đó, suy ra $\overrightarrow{a}\perp \overrightarrow{b}\iff$$a_1{b}_1+a_2{b}_2+a_3{b}_3=0$

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Ôn tập chương 3 (mới 2024 + Bài Tập) – Toán 12 

50 Bài tập Hệ tọa độ trong không gian Toán 12 mới nhất

TOP 40 câu Trắc nghiệm Hệ tọa độ trong không gian (có đáp án 2024) - Toán 12