Trong không gian Oxyz, cho mặt cầu (S):$(x+1{)}^2+(y-1{)}^2+(z+2{)}^2=2$và hai đường thẳng d:$\frac{x-2}{1}=\frac{y}{2}=\frac{z-1}{-1}$,Δ:$\frac{x}{1}=\frac{y}{1}=\frac{z-1}{-1}$. Phương trình nào dưới đây là phương trình mặt phẳng tiếp xúc với (S) và song song với d và Δ

Cho hàm số f(x)=|$2x^3-3x^2+m$|. Có bao nhiêu số nguyên m để $mi{n}_{[-1;3]} f\left(x\right)\le 3$

Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a và BC=a$\sqrt{2}$ (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AB và SC là

Cho ba số thực dương a,b,c theo thứ tự lập thành một cấp số nhân và a+b+c=64. Giá trị biểu thức $P={\log }_2\left(ab+bc+ca\right)-{\log }_{2}abc$  bằng

Trong không gian Oxyz, cho hai điểm A(1;-2;-3),B(-1;4;1). Đường thẳng qua trung điểm của đoạn thẳng AB và song song với đường thẳng d:$\frac{x+2}{1}=\frac{y-2}{-1}=\frac{z+3}{2}$ là

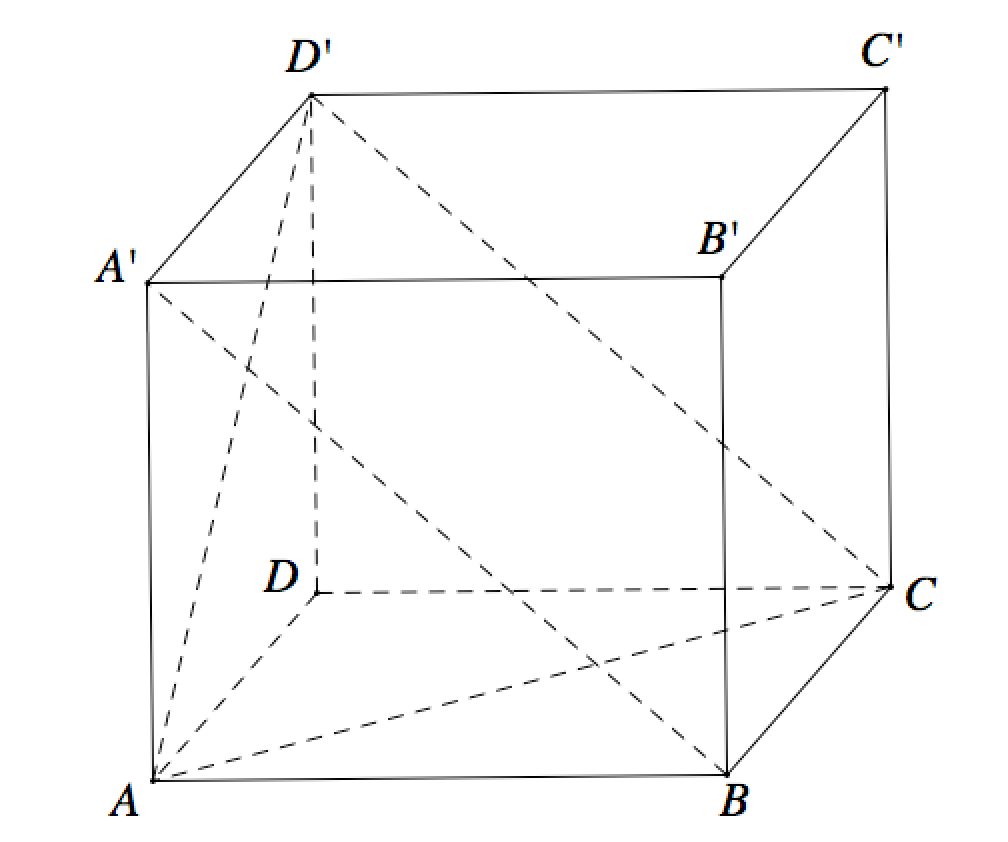
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=$\sqrt{3}$. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng

Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M,N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD=2CP. Mặt phẳng (MNP) cắt AD tại Q. Tính thể tích khối đa diện BMNPQD

Một hộp chứa 11 quả cầu gồm 5 quả cầu màu xanh và 6 quả cầu màu đỏ. Chọn ngẫu nhiên đồng thời 2 quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng

Trong không gian Oxyz, một véctơ pháp tuyến của mặt phẳng (Oxy) là

Cho ${\int }_2^3\sqrt{x-\frac{4}{x^2}}\left(1+\frac{8}{x^3}\right)dx=\frac{a\sqrt{23}-b}{c}$ với a,b,c là các số nguyên dương, a/c tối giản. Giá trị biểu thức a+b+c bằng

Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Tang của góc giữa đường thẳng AB′ và mặt phẳng (ACC′A′) bằng

Cho hình phẳng (H) giới hạn bởi đường cong (C):$y=e^x$, tiếp tuyến của (C) tại điểm M(1;e) và trục Oy. Diện tích của (H) bằng

Tổng các nghiệm của phương trình ${\log }_{2}x+{\log }_{2}x.{\log }_{4}x=\frac{3}{2}$ là

Hàm số $y=\frac{3x+1}{x+1}$ có bao nhiêu điểm cực trị

Có bao nhiêu số nguyên dương m để hàm số $y=x^4-m{x}^2$ đồng biến trên khoảng (1;+∞).

Khi đồ thị hàm số $y=x^3-3mx+2$ có hai điểm cực trị A, B và đường tròn (C):$(x-1{)}^2+(y-1{)}^2=3$ cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN