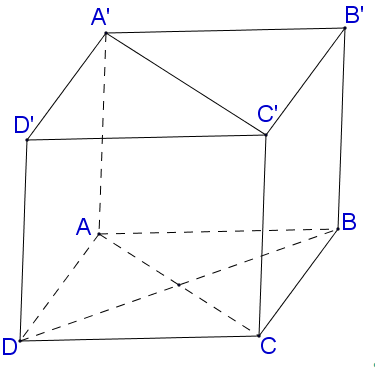
Hình hộp đứng ABCD.A′B′C′D′ có đáy là hình thoi. Diện tích các tứ giác ABCD,ACC′A′,BDD′B′ lần lượt là ${\mathrm{S}}_1,{\mathrm{S}}_2,{\mathrm{S}}_3.$ Khi đó thể tích khối hộp ABCD.A′B′C′D′ là

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $\mathrm{y}={\mathrm{x}}^3-3{\mathrm{x}}^2+1,$ trục tung và tiếp tuyến tại điểm có tọa độ thỏa mãn y'' = 0

Số nghiệm của phương trình $5^{3-{\log }_5\mathrm{x}}=25\mathrm{x}$ là

Có 5 học sinh không quen biết nhau cùng đến một cửa hàng kem có 6 quầy phục vụ. Xác suất để có 3 học sinh cùng vào 1 quầy và 2 học sinh còn lại vào 1 quầy khác là

Cho ${\int }^{\text{}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\frac{4}{\sqrt{{\mathrm{x}}^2+1}}+\mathrm{C}.$ Khi đó ${\int }^{\text{}}\mathrm{f}\left(2\mathrm{x}\right)\mathrm{dx}$ bằng

Cho hình chóp S.ABCD có đáy là hình vuông, BD = 2a. Tam giác SAC vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối cầu ngoại tiếp hình chóp là

Nếu $\lg 2=\mathrm{a}$ thì $\lg 4000$ bằng

Cho khối lăng trụ có thể tích bằng ${\mathrm{a}}^3$ và diện tích đáy bằng ${\mathrm{a}}^2$. Chiều cao h của khối lăng trụ (T) là

Tập nghiệm của bất phương trình ${\log }_2\left({\mathrm{x}}^2-3\mathrm{x}\right)>2$ là

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng 2, $\widehat{\mathrm{ABC}}={60}^0.$ Biết $\mathrm{SO}\perp \left(\mathrm{ABCD}\right)$ và thể tích khối chóp S.ABCD bằng 2. Tính SA.

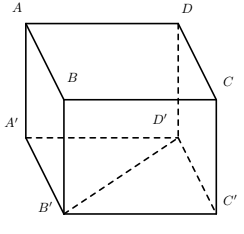
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AA'  và B'D' bằng

Trong mặt phẳng Oxy, cho đường thẳng d có phương trình $3\mathrm{x}-\mathrm{y}+2=0$. Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng trục Oy

Một chiếc cốc hình trụ có chiều cao 5R, bán kính đáy R. Đặt vào trong cốc 2 quả bóng hình cầu có bán kính R. Gọi ${\mathrm{V}}_1$ là phần không gian mà 2 quả bóng chiếm chỗ và ${\mathrm{V}}_2$ là phần không gian còn lại trong cốc. Tính tỉ số $\frac{{\mathrm{V}}_1}{{\mathrm{V}}_2}.$

Cho hàm số $\mathrm{y}={\sin }^4\mathrm{x}+{\cos }^4\mathrm{x}$$+\mathrm{msinxcosx}.$ Tìm các giá trị thực của m để hàm số có GTLN=2.

Biết thể tích khí ${\mathrm{CO}}_2$ năm 1993 là $\mathrm{V}\left({\mathrm{m}}^3\right)$. 10 năm tiếp theo, mỗi năm thể tích khi ${\mathrm{CO}}_2$ tăng m% ; 20 năm tiếp theo nữa, mỗi năm thể tích khí ${\mathrm{CO}}_2$ tăng n%. Tính thể tích khí ${\mathrm{CO}}_2$ năm 2017?

Cho hình chóp S.ABCD có đáy là hình thoi, $\widehat{\mathrm{BAD}}={60}^0$, SA⊥(ABCD). Mệnh đề nào sau đây là SAI?