Câu hỏi:
16/07/2024 260Giải bất phương trình (x2 - 4)(x - 3) ≥ 0 ta được?
A. -2 ≤ x ≤ 2 hoặc x ≥ 3.
B. x ≤ 2 hoặc x ≥ 3.
C. x ≥ 3
D. x ≤ -2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: A
Giải thích:
Lời giải:
Ta có (x2 - 4)(x - 3) ≥ 0
⇔ (x - 2)(x + 2)(x - 3) ≥ 0
Ta có
x - 2 = 0 ⇔ x = 2; x - 3 = 0
⇔ x = 3; x + 2 = 0 ⇔ x = -2
Bảng xét dấu:
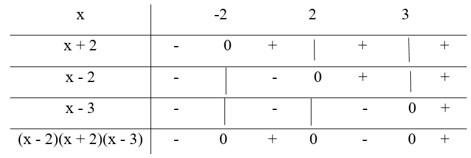
Từ bảng xét dấu ta có
(x2 - 4)(x - 3) ≥ 0
⇔ -2 ≤ x ≤ 2 hoặc x ≥ 3.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Kết luận nào sau đây là đúng khi nói về nghiệm của bất phương trình (x + 3)(x + 4) > (x - 2)(x + 9) + 25?
Câu 3:
Biểu diễn tập nghiệm của bất phương trình x > 8 trên trục số, ta được?
Câu 4:
Biểu diễn tập nghiệm của
bất phương trình x ≥ 8 trên trục số, ta được?
Câu 5:
Với những giá trị nào của x thì giá trị của
biểu thức (x + 1)2 - 4 không lớn hơn giá trị của biểu thức (x - 3)2?
Câu 6:
Với điều kiện nào của x thì biểu thức
B =2x−43−x nhận giá trị âm?
Câu 7:
Giá trị của x để biểu thức
P = x−3x+1 có giá trị không lớn hơn 1?
Câu 11:
Bất phương trình x - 2 < 1 tương đương với bất phương trình sau?
Câu 12:
Nghiệm của bất phương trình
(x + 3) (x + 4) > (x - 2)(x + 9) + 25 là?
Câu 14:
Hãy chọn câu đúng, x = -3 không là nghiệm của bất phương trình nào dưới đây











