Câu hỏi:
23/07/2024 604Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
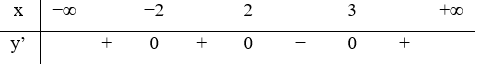
Số điểm cực trị của hàm số y=g(x)=f(1-x2) là
A. 5
B. 0
C. 3
D. 1
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn
Do đó
Phương trình là nghiệm đơn
Vậy hàm số đã cho có duy nhất 1 điểm cực trị.
Chọn D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Hàm số y = f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x+1) có bao nhiêu điểm cực trị?
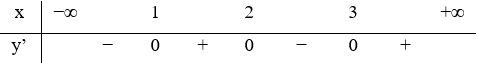
Câu 3:
Hàm số y=f(x) xác định, liên tục trên R\{0} và có bảng xét dấu đạo hàm như hình vẽ.
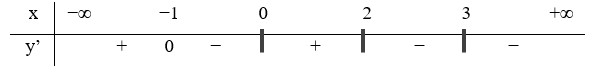
Hỏi hàm số có bao nhiêu điểm cực trị?
Câu 5:
Hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số y=f(-x+1) đạt cực đại tại điểm
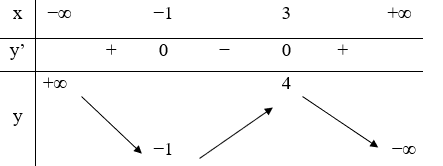
Câu 6:
Đồ thị của hàm số y = -x3 + 3x +5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.
Câu 7:
Cho hàm số y=f(x) có bảng biến thiên như sau
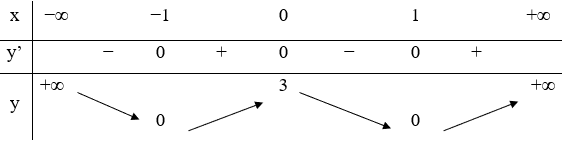
Mệnh đề nào dưới đây sai?
Câu 8:
Biết hàm số (C): có hai điểm cực trị là x1,x2. Đẳng thức nào sau đây đúng?
Câu 9:
Hàm số y=f(x) xác định, liên tục trên đoạn [2;4] và có bảng biến thiên như sau
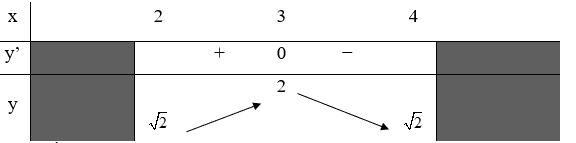
Mệnh đề nào sau đây đúng?
Câu 10:
Cho hàm số y = f(x) có đạo hàm f'(x) = x2019(x2020 - 1), . Hỏi hàm số có bao nhiêu điểm cực trị?
Câu 12:
Hàm số y=f(x) liên tục trên và có bảng xét dấu đạo hàm như hình vẽ.
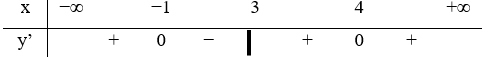
Số điểm cực trị của hàm số y = g(x) = f(x2+2x+3) là
Câu 13:
Hàm số y =f(x) liên tục trên và có bảng biến thiên như hình vẽ.
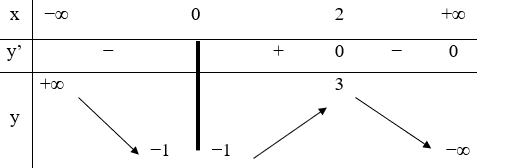
Khẳng định nào sau đây là khẳng định đúng?
Câu 15:
Hàm số y=f(x) xác định, liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
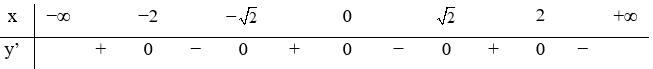
Hàm số y = f(-x) có bao nhiêu điểm cực trị?


