Câu hỏi:
14/11/2024 124
Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc?
Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc?
A. 120.
B. 1.
C. 5.
D. 25.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải:
Số cách sắp xếp 5 học sinh thành một hàng dọc là
*Phương pháp giải:
- Số cách xếp 5 học sinh thành một hàng dọc là một hoán vị của 5 phần tử: Pn = n(n-1)...2.1 = n!
*Lý thuyến cần nắm về tổ hợp - xác suất
1. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.
2. Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
3. Hoán vị:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.
- Số các hoán vị của n phần tử là: Pn = n(n-1)...2.1 = n!
4. Chỉnh hợp:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
- Số các chỉnh hợp chập k của n phần tử là:
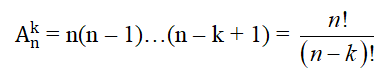
5. Tổ hợp:
Giả sử A có n phần tử (n ≥ 1).
- Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
Số các tổ hợp chập k của n phần tử là:
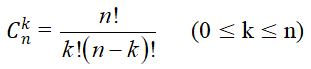
6. Công thức nhị thức Niu-tơn:
(a + b)n = Cn0an + Cn1an - 1b + … + Cnkan - kbk + … + Cnn-1abn-1 + Cnnbn
7. Phép toán trên các biến cố:
- Giả sử A là biến cố liên quan đến một phép thử.
Khi đó, tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A−.
- Giả sử A và B là hai biến cố liên quan đến một phép thử:
+ Tập A ⋃ B được gọi là hợp của các biến cố A và B.
+ Tập A ⋂ B được gọi là giao của các biến cố A và B.
+ Nếu A ⋂ B = ∅ thì ta nói A và B xung khắc.
8. Xác suất của biến cố:
Giả sử A là biến cố liên quan đến phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, xác suất của biến cố A là: 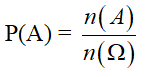
trong đó: n(A) là số phần tử của A; còn n(Ω) là số các kết quả có thể xảy ra của phép thử.
9. Tính chất của xác suất:
Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện.
P(∅) = 0, P(Ω) = 1
0 ≤ P(A) ≤ 1, với mọi biến cố A.
Nếu A và B xung khắc, thì P(AB) = P(A) + P(B) (công thức cộng xác suất)
Với mọi biến cố A, ta có: P(A−) = 1 – P(A).
A và B là hai biến cố độc lập khi và chỉ khi P(A.B) = P(A).P(B).
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Tổ hợp - xác suất hay, chi tiết
Đáp án đúng: A
*Lời giải:
Số cách sắp xếp 5 học sinh thành một hàng dọc là
*Phương pháp giải:
- Số cách xếp 5 học sinh thành một hàng dọc là một hoán vị của 5 phần tử: Pn = n(n-1)...2.1 = n!
*Lý thuyến cần nắm về tổ hợp - xác suất
1. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.
2. Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
3. Hoán vị:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.
- Số các hoán vị của n phần tử là: Pn = n(n-1)...2.1 = n!
4. Chỉnh hợp:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
- Số các chỉnh hợp chập k của n phần tử là:
5. Tổ hợp:
Giả sử A có n phần tử (n ≥ 1).
- Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
Số các tổ hợp chập k của n phần tử là:
6. Công thức nhị thức Niu-tơn:
(a + b)n = Cn0an + Cn1an - 1b + … + Cnkan - kbk + … + Cnn-1abn-1 + Cnnbn
7. Phép toán trên các biến cố:
- Giả sử A là biến cố liên quan đến một phép thử.
Khi đó, tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A−.
- Giả sử A và B là hai biến cố liên quan đến một phép thử:
+ Tập A ⋃ B được gọi là hợp của các biến cố A và B.
+ Tập A ⋂ B được gọi là giao của các biến cố A và B.
+ Nếu A ⋂ B = ∅ thì ta nói A và B xung khắc.
8. Xác suất của biến cố:
Giả sử A là biến cố liên quan đến phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, xác suất của biến cố A là:
trong đó: n(A) là số phần tử của A; còn n(Ω) là số các kết quả có thể xảy ra của phép thử.
9. Tính chất của xác suất:
Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện.
P(∅) = 0, P(Ω) = 1
0 ≤ P(A) ≤ 1, với mọi biến cố A.
Nếu A và B xung khắc, thì P(AB) = P(A) + P(B) (công thức cộng xác suất)
Với mọi biến cố A, ta có: P(A−) = 1 – P(A).
A và B là hai biến cố độc lập khi và chỉ khi P(A.B) = P(A).P(B).
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Tổ hợp - xác suất hay, chi tiết
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
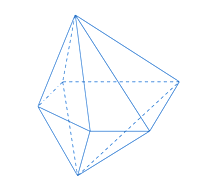
Cho hình bát diện đều cạnh 4a. Gọi S là tổng diện tích của tất cả các mặt của hình bát diện đều đó. Khi đó S bằng:
Cho hình bát diện đều cạnh 4a. Gọi S là tổng diện tích của tất cả các mặt của hình bát diện đều đó. Khi đó S bằng:
Câu 3:
Cho khối cầu (T) có tâm O bán kính R. Gọi S và V lần lượt là diện tích mặt cầu và thể tích khối cầu. Mệnh đề nào sau đây là đúng?
Câu 4:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đồng biến trên khoảng Số phần tử của tập S là
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đồng biến trên khoảng Số phần tử của tập S là
Câu 5:
Cho phương trình . Bằng cách đặt phương trình đã cho trở thành phương trình nào dưới đây?
Cho phương trình . Bằng cách đặt phương trình đã cho trở thành phương trình nào dưới đây?
Câu 6:
Cho hàm số y= f(x) liên tục trên đoạn [-3; 4] và có đồ thị như hình vẽ.
![Cho hàm số y= f(x) liên tục trên đoạn [-3; 4] và có đồ thị như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/04/blobid0-1650090758.png)
Gọi M và m lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-3; 1]. Tích M.n bằng
Câu 7:
Cho hàm số f(x) có đồ thị như hình vẽ.
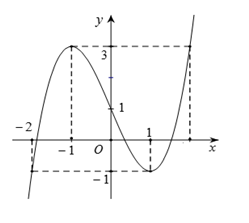
Hàm số đã cho đồng biến trên khoảng nào?
Câu 9:
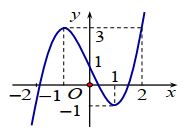
Cho hàm số f(x). Hàm số y = f'(x) có đồ thị như hình bên.
Hỏi hàm số đồng biến trên khoảng nào dưới đây?
Câu 11:
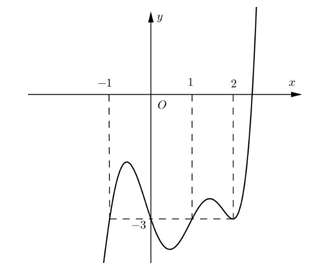
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình vẽ dưới đây.
Tập hợp tất cả các giá trị thực của tham số m để phương trình có nghiệm là
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình vẽ dưới đây.

Tập hợp tất cả các giá trị thực của tham số m để phương trình có nghiệm là
Câu 12:
Cho hàm số y = f(x) có đạo hàm Khi đó số điểm cực trị của hàm số là
Cho hàm số y = f(x) có đạo hàm Khi đó số điểm cực trị của hàm số là
Câu 14:
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) trên trục Oz có tọa độ là
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) trên trục Oz có tọa độ là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)