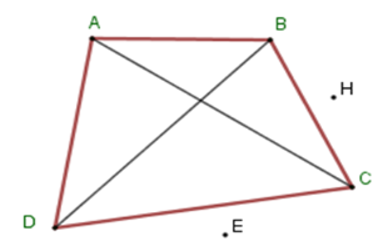
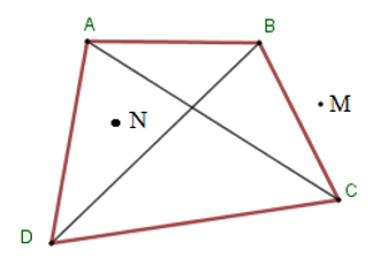
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất.

Đáp án đúng là: C

*Phương pháp giải: Sử dụng quan hệ giữa ba cạnh của một tam giác, hệ thức cộng đoạn thẳng.

*Lời giải:

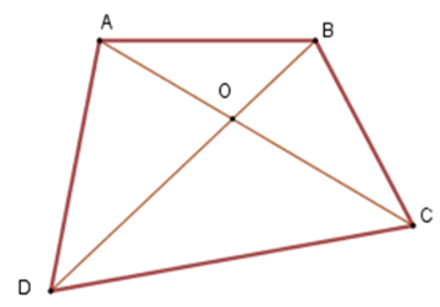
+ Xét tam giác OAB ta có OA + OB > AB (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).

Tương tự ta có OC + OD > CD; OB + OC > BC; OA + OD > AD

Cộng vế với vế ta được

OA + OB + OC + OD + OB + OC + OA + OD > AB + BC + CD + AD

$\iff$2(OA + OB + OC + OD) > AB + BC + CD + DA

$\iff$ OA + OB + OC + OD > $\frac{AB\text{}+BC+CD+DA}{2}$ nên B đúng

+ Xét tam giác ABC cs AB + BC > AC (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).

Tương tự ta có BC + CD > BD;

CD + DA > AC;

AD + DB > BD

Cộng vế với vế ta được

AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD

$\iff$ 2(AB + BC + CD + DA) > 2(AC + BD)

$\iff$ AB + BC + CD + DA > AC + BD

mà AC + BD = OA + OC + OB + OD nên

OA + OB + OC + OD < AB + BC + CD + DA nên A đúng

Vậy cả A, B đều đúng.

* Một số lý thuyết liên quan:

Định lí 1: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Nhận xét

+ Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh đối diện với vuông góc (tức là cạnh huyền) là cạnh lớn nhất.

+ Tương tự trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Bất đẳng thức tam giác

Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.

Cho tam giác ABC, ta có các bất đẳng thức sau:

• AB + AC > BC hay b + c > a

• AB + BC > AC hay c + a > b

• AC + BC > AB hay b + a > c

Hệ quả của bất đẳng thức tam giác

Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại.

Nhận xét: Nếu xét đồng thời cả tổng và hiệu độ dài hai cạnh của một tam giác thì quan hệ giữa các cạnh của nó còn được phát biểu như sau:

Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

Ví dụ: Trong tam giác ABC, với cạnh BC ta có:

|AC - AB| < BC < AC + AB hay |b - c| < a < b + c

Xem thêm các bài viết liên quan hay, chi tiết:

Giải Toán 7 Bài 33 (Kết nối tri thức): Quan hệ giữa ba cạnh của một tam giác

Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác có đáp án - Toán lớp 7

Lý thuyết Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác – Toán 7 Cánh diều