Câu hỏi:
15/07/2024 228Tứ giác ABCD có = 900. Chọn câu đúng
A. AC2 + BD2 = AB2 – CD2
B. AC2 + BD2 = AB2 + CD2
C. AC2 + BD2 = 2AB2
D. Cả A, B, C đều sai
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: B
Giải thích:
Lời giải
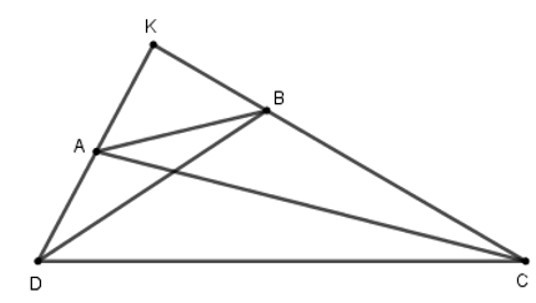
Gọi K là giao điểm AD, BC.
Vì = 900 nên = 900.
Xét ΔKAC vuông tại K ta có:
AC2 = KC2 + KA2.
Xét ΔKBD vuông tại K ta có:
BD2 = KB2 + KD2.
Xét ΔKBA vuông tại K ta có:
BA2 = KA2 + KB2.
Xét ΔKBD vuông tại K ta có:
CD2 = KC2 + KD2.
Từ đó BD2 + AC2
= KC2 + KA2 + KB2 + KD2
= (KB2 +KA2) + (KD2 + KC2)
= AB2 + DC2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất.
Câu 3:
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 2000. Tổng số đo các góc ngoài tại 2 đỉnh A, C là:
Câu 4:
Tứ giác ABCD có AB = BC, CD = DA, = 900; = 1200. Hãy chọn câu đúng nhất
Câu 6:
Cho tứ giác ABCD có = 500; = 1500; = 450. Số đo góc ngoài tại đỉnh B bằng:
Câu 7:
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là
Câu 8:
Cho tứ giác ABCD biết số đo của các góc ; ; ; tỉ lệ thuận với 4; 9; 7; 6.
Khi đó số đo các góc ; ; ; lần lượt là:
Câu 11:
Cho tứ giác ABCD có = 500; = 1170; = 710. Số đo góc ngoài tại đỉnh D bằng
Câu 13:
Cho tứ giác ABCD biết số đo của các góc tỉ lệ thuận với 4; 3; 5; 6
Câu 15:
Tam giác ABC có = 600, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc ; .