Câu hỏi:
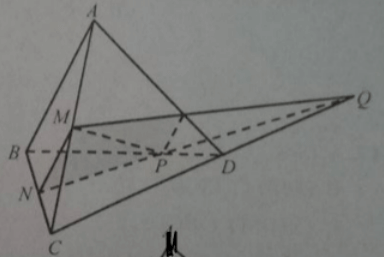
12/10/2024 5,064Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Giao tuyến của hai mặt phẳng (MNP) và (ACD) là:
A. MP
B. NQ
C. MQ
D. AP
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
*Phương pháp giải:
Cách xác định giao tuyến của hai mặt phẳng:
- Nếu hai đường thẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó.
- Giao tuyến là đường thẳng chung của hai mặt phẳng, tức là giao tuyến là đường thẳng thuộc cả hai mặt phẳng.
- Khi tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung thuộc cả hai mặt phẳng. Đường thẳng đi qua hai điểm chung này chính là giao tuyến cần tìm.
- Điểm đầu tiên của giao tuyến thường là một điểm dễ nhận thấy vì nằm trên cả hai mặt phẳng đã cho.
- Điểm thứ hai của giao tuyến được xác định bằng cách xác định hai đường thẳng cùng đi qua điểm đó, nằm trên cùng một mặt phẳng thứ ba và không song song với hai mặt phẳng đã cho. Điểm thứ hai của giao tuyến là giao điểm của hai đường thẳng này.
*Lời giải:
(MNP) ∩ (ACD) = (MNQ) ∩ (ACD) = MQ.
* Một số lý thuyết liên quan:
Phương pháp tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song với nhau
Giả sử . Tìm giao tuyến của (P) và (Q)
Bước 1: Tìm 1 điểm chung M của (P) và (Q)
Bước 2: Ta có:
Kết luận: Giao tuyến của (P) và (Q) là đường thẳng d, với d đi qua M và d // a // b.
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Nhận biết)
50 Bài tập Đại cương về đường thẳng và mặt phẳng Toán 11 mới nhất
50 bài tập Đại cương về đường thẳng (có đáp án 2024) và cách giải
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên các cạnh AB, AC, BD sao cho EF cắt BC tại M, EG cắt AD tại N. tìm mệnh đề sai trong các mệnh đề sau đây?
Câu 2:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số EJ/IF bằng
Câu 3:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Đường thẳng MP không chéo với đường thẳng nào sau đây?
Câu 4:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IJ/JB bằng:
Câu 5:
Cho hình tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện đi qua ba điểm M, N, P là:
Câu 6:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Tỉ số QD/QC bằng:
Câu 7:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD). Tỉ số IA/IF bằng:
Câu 8:
Cho hình lăng trụ ABC.A’B’C’ đáy là tam giác đều tâm O, C’O vuông góc với (ABC). Khoảng cách từ O tới đường thẳng CC’ bằng a. Góc tạo bởi mặt phẳng (AA’C’C) và mp(BB’C’C) bằng . Gọi góc giữa cạnh bên và đáy của lẳng trụ là φ thì.
Câu 9:
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng cạnh bên bằng a. Khoảng cách từ AD tới (SBC) bằng:
Câu 11:
Cho hình chóp S.ABCD, các cặp đường thẳng nào sau đây chéo nhau?
Câu 12:
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là .
Tìm câu đúng nhất.
Thiết diện của hình tứ diện cắt bởi mặt phẳng () là:
Câu 14:
Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh bằng a, cạnh bên hình chóp cũng bằng a. gọi I là trung điểm của SA. Mặt phẳng (IBC) cắt hình chóp theo thiết diện CBIJ. Chu vi thiết diện CBIJ bằng:
Câu 15:
Cho hình chóp S.ABCD, đáy hình thang ABCD có đáy lớn AD. Trong các mệnh đề sau mệnh đề nào sai?
