Câu hỏi:
22/07/2024 619
Cho tam giác ABC có hai đường phân giác AD và BE cắt nhau tại G. Khi đó:
Cho tam giác ABC có hai đường phân giác AD và BE cắt nhau tại G. Khi đó:
A. Điểm G cách đều ba đỉnh của ∆ABC;
B. Điểm G cách đều ba cạnh của ∆ABC;
C. GE = GD;
D. Tất cả các đáp án đều sai.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
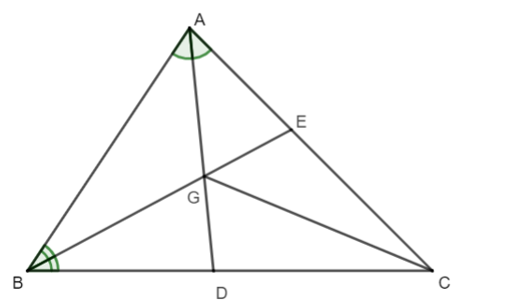
Ta có ∆ABC có hai đường phân giác AD và BE cắt nhau tại G.
Do đó điểm G là điểm cách đều ba cạnh của ∆ABC.
Hướng dẫn giải
Đáp án đúng là: B

Ta có ∆ABC có hai đường phân giác AD và BE cắt nhau tại G.
Do đó điểm G là điểm cách đều ba cạnh của ∆ABC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho tam giác ABC có hai đường phân giác AD và BE cắt nhau tại G. Khi đó CG là
Cho tam giác ABC có hai đường phân giác AD và BE cắt nhau tại G. Khi đó CG là
Câu 5:
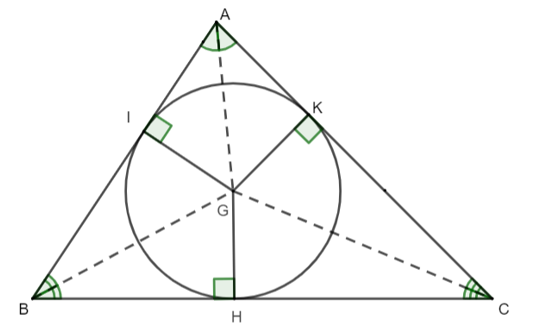
Cho hình vẽ như bên dưới. Biết GK = 3x − 8 và GH = x + 4. Khi đó giá trị của x bằng:
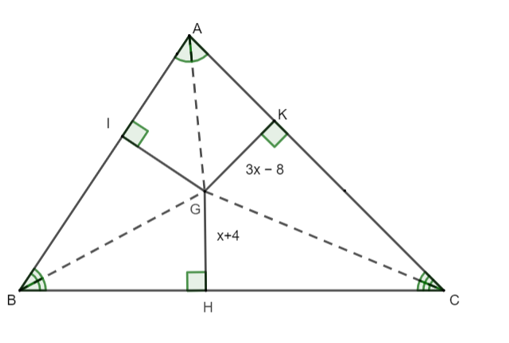
Cho hình vẽ như bên dưới. Biết GK = 3x − 8 và GH = x + 4. Khi đó giá trị của x bằng:

Câu 6:
Cho hình vẽ như bên dưới. Biết GI = 8 cm. Độ dài đoạn thẳng GH bằng:
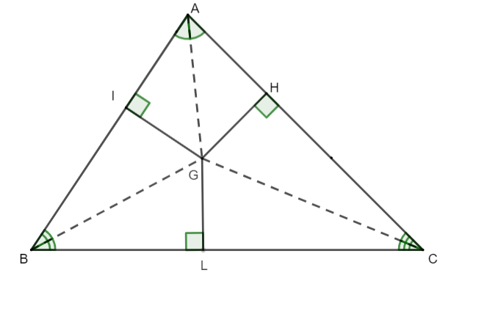
Cho hình vẽ như bên dưới. Biết GI = 8 cm. Độ dài đoạn thẳng GH bằng:

Câu 7:
Cho ∆ABC cân tại A có BD và CE là hai đường phân giác cắt nhau tại F. Tia AF cắt BC tại G. Khi đó điểm G:
Cho ∆ABC cân tại A có BD và CE là hai đường phân giác cắt nhau tại F. Tia AF cắt BC tại G. Khi đó điểm G:
Câu 8:
Cho ∆ABC có trọng tâm G và I là giao của ba đường phân giác của tam giác ∆ABC. Biết B; G; I thẳng hàng. Khi đó ΔABC là tam giác gì?
Cho ∆ABC có trọng tâm G và I là giao của ba đường phân giác của tam giác ∆ABC. Biết B; G; I thẳng hàng. Khi đó ΔABC là tam giác gì?
Câu 9:
Trong một tam giác cân, đường phân giác xuất phát từ đỉnh cũng là:
Trong một tam giác cân, đường phân giác xuất phát từ đỉnh cũng là:
Câu 10:
Điền vào chỗ trống: “Giao điểm của ba đường phân giác trong một tam giác …”
Điền vào chỗ trống: “Giao điểm của ba đường phân giác trong một tam giác …”
Câu 12:
Điền vào chỗ trống sau: “Ba đường phân giác đi qua một điểm. Điểm này cách đều … của tam giác”.
Điền vào chỗ trống sau: “Ba đường phân giác đi qua một điểm. Điểm này cách đều … của tam giác”.
Câu 13:
Cho hình vẽ như bên dưới. Biết đường kính của đường tròn nằm trong tam giác là 8 cm. Độ dài của GK bằng: