Câu hỏi:
22/07/2024 388
Cho tam giác A1B1C1 có diện tích là 3 (đơn vị diện tích). Dựng tam giác A2B2C2 bằng cách nối các trung điểm của các cạnh B1C1, C1A1, A1B1. Tiếp tục quá trình này, ta có các tam giác A3B3C3, ..., AnBnCn,... Kí hiệu sn là diện tích của tam giác AnBnCn.
a) Tính sn.
Cho tam giác A1B1C1 có diện tích là 3 (đơn vị diện tích). Dựng tam giác A2B2C2 bằng cách nối các trung điểm của các cạnh B1C1, C1A1, A1B1. Tiếp tục quá trình này, ta có các tam giác A3B3C3, ..., AnBnCn,... Kí hiệu sn là diện tích của tam giác AnBnCn.
a) Tính sn.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a)
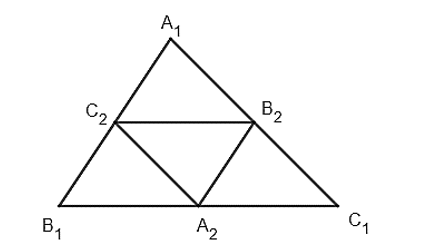
Theo cách xác định tam giác A2B2C2, ta có s2 = s1.
Tương tự, s3 = s2, ...., .
Vậy .
a)

Theo cách xác định tam giác A2B2C2, ta có s2 = s1.
Tương tự, s3 = s2, ...., .
Vậy .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 7:
Cho dãy số (un) với u1 = 2, , n ≥ 1. Đặt vn = un + 1 – un.
a) Tính v1 + v2 + ... + vn theo n.
Cho dãy số (un) với u1 = 2, , n ≥ 1. Đặt vn = un + 1 – un.
a) Tính v1 + v2 + ... + vn theo n.
Xem đáp án »
22/07/2024
201


