Giải SBT Toán lớp 11 – KNTT – Tập 1 Bài 15. Giới hạn của dãy số
-
86 lượt thi
-
18 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 7:
22/07/2024Cho với a, b là các số thực thỏa mãn |a| < 1, |b| < 1. Tính .
Xem đáp án
Áp dụng công thức tính tổng n số hạng đầu của cấp số nhân, ta có:
Do đó, (do |a| < 1, |b| < 1).
Câu 8:
22/07/2024Tính .
Xem đáp án
Ta có 1, 3, 5, ..., 2n – 1 là một cấp số cộng gồm n số hạng và có số hạng đầu u1 = 1, công sai d = 2.
Khi đó, 1 + 3 + 5 + ... + (2n – 1) = .
Do đó, .
Câu 9:
22/07/2024 Xem đáp án
Nhận thấy S là tổng của cấp số nhân lùi vô hạn (un) với số hạng đầu u1 = – 1 và công bội q = .
Do đó, .
Câu 10:
22/07/2024Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:
a) 1,(03); Xem đáp án
a) 1,(03) = 1 + 0,03 + 0,0003 + ... + 0,00...03 + ...
Câu 11:
22/07/2024Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:
b) 3,(23).
Xem đáp án
b) 3,(23) = 3 + 0,23 + 0,0023 + ... + 0,00...23 + ...
.
Câu 13:
22/07/2024Cho tam giác A1B1C1 có diện tích là 3 (đơn vị diện tích). Dựng tam giác A2B2C2 bằng cách nối các trung điểm của các cạnh B1C1, C1A1, A1B1. Tiếp tục quá trình này, ta có các tam giác A3B3C3, ..., AnBnCn,... Kí hiệu sn là diện tích của tam giác AnBnCn.
a) Tính sn.
Xem đáp án
a)
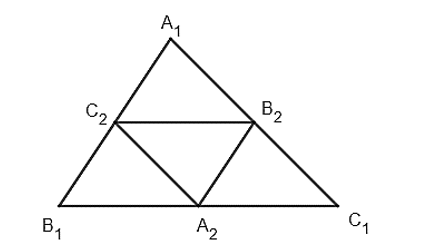
Theo cách xác định tam giác A2B2C2, ta có s2 = s1.
Tương tự, s3 = s2, ...., .
Vậy .
Câu 14:
22/07/2024b) Tính tổng s1 + s2 + ... + sn + ...
Xem đáp án
b) Ta có s1 + s2 + ... + sn + ... là tổng của cấp số nhân lùi vô hạn có số hạng đầu u1 = 3 và công bội q = . Do đó
s1 + s2 + ... + sn + ... = .
Câu 15:
22/07/2024Cho dãy số (un) với u1 = 2, , n ≥ 1. Đặt vn = un + 1 – un.
a) Tính v1 + v2 + ... + vn theo n.
Xem đáp án
a) Ta có vn = un + 1 – un = .
Do đó, v1 + v2 + ... + vn =
.
Câu 16:
22/07/2024 Xem đáp án
b) Ta có v1 + v2 + ... + vn = (u2 – u1) + (u3 – u2) + ... + (un + 1 – un)
= un + 1 – u1 = .
Mà theo câu a có v1 + v2 + ... + vn = .
Do đó, . Từ đó suy ra .
Câu 18:
23/07/2024Cho dãy số (un) có tính chất . Tính .
Xem đáp án
Ta có , mà khi n → +∞ nên .
Mặt khác, .
Vậy = 1.