Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB = AC = 6, BC = 8. Khoảng cách từ O đến mặt phẳng (ABC) bằng 2. Thể tích khối cầu (S) bằng

Xét hàm số f(x) liên tục trên đoạn [0;1] và thỏa mãn 2f(x) + 3f(1 - x) =$\sqrt{1-\mathrm{x}}$. Giá trị của tích phân ${\int }_0^1\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$ bằng: 

Cho hàm số y = f(x) có bảng biến thiên sau:

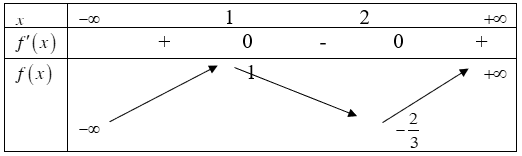
Số nghiệm của phương trình 4f(x) + 3 = 0 là

Cho số phức z = x + yi (x, y ∈ R) thỏa mãn z+1-2i-$\left|z\right|$(1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây? 

Với hai số phức ${\mathrm{z}}_{1 }\mathrm{và} {\mathrm{z}}_2$ thỏa mãn ${\mathrm{z}}_1+{\mathrm{z}}_2=8+6\mathrm{i}$ và $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=2$. Tim giá trị lớn nhất của biểu thức $\mathrm{P}=\left|{\mathrm{z}}_1\right|+\left|{\mathrm{z}}_2\right|$.

Cho hình lăng trụ đứng ABC.A' B' C' có AB = AC = a, $\stackrel{\wedge }{BAC}$ = 120⁰, AA' = a. Gọi M, N lần lượt là trung điểm của B'C' và CC'. Số đo góc giữa mặt phẳng (AMN) và mặt phẳng (ABC) bằng:

Cho số phức z = -2 + 3i. Số phức liên hợp của z là: 

Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1) = 3, F(3) = 5 và${\int }_1^3({\mathrm{x}}^4-8\mathrm{x})\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=12.$ Tính $\mathrm{I}={\int }_1^3({\mathrm{x}}^3-2)\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}.$

Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^4-4{\mathrm{x}}^3+2{\mathrm{x}}^2-\mathrm{x}+1$,∀ x∈ R. Tính${\int }_0^1{\mathrm{f}}^2\left(\mathrm{x}\right).{\mathrm{f}}^{\text{'}}\left(\mathrm{x}\right)\mathrm{dx}$.  

Cho hình phẳng D giới hạn bởi đường cong $\mathrm{y}=\sqrt{2-\mathrm{sinx}}$ , trục hoành và các đường thẳng x = 0, $\mathrm{x}=\frac{\mathrm{\pi }}{2}$. Khối tròn xoay tạo thành D quay quanh trục hoành có thể tích V bằng: 

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a, tam giác SAB và tam giác SCB lần lượt vuông tại A, C. Khoảng cách từ S đến mặt phẳng (ABC) bằng 2a. Cosin của góc giữa hai mặt phẳng (SAB) và (SCB) bằng:

Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là 48. Trên các cạnh SA, SB, SC, SD lần lượt lấy các điểm A', B', C' và D' sao cho $\frac{\mathrm{SA}\text{'}}{\mathrm{SA}}=\frac{\mathrm{SC}\text{'}}{\mathrm{SC}}=\frac{1}{3}$ và $\frac{\mathrm{SB}\text{'}}{\mathrm{SB}}=\frac{\mathrm{SD}\text{'}}{\mathrm{SD}}=\frac{3}{4}$. Tính thể tích V của khối đa diện lồi S.A'B'C'D'.  

Biết $\lim \frac{{\mathrm{an}}^3-5{\mathrm{n}}^2+1}{1-2{\mathrm{n}}^3}=-\frac{3}{2}$ với a là tham số. Lúc đó ${\mathrm{a}}^3-\mathrm{a}$ bằng:

Trong không gian Oxyz, cho điểm A(3;5;2). Phương trình đường thẳng nào dưới đây là phương trình của mặt phẳng đi qua các điểm là hình chiếu của điểm A trên các mặt phẳng tọa độ?

Cho tam giác ABC, lấy điểm M trên BC sao cho $\overrightarrow{\mathrm{MB}}=4\overrightarrow{\mathrm{MC}}$. Chọn khẳng định đúng.

Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng (d):$\frac{\mathrm{x}-2}{2}=\frac{\mathrm{y}+2}{-1}=\frac{\mathrm{z}-3}{1}$. Gọi điểm B thuộc trục Ox sao cho AB vuông góc với đường thẳng (d). Khoảng cách từ B đến mặt phẳng ($\alpha$): 2x + 2y - z - 1 = 0 là: