Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAB) tạo với (SBC) một góc ${60}^o$ và mặt phẳng (SAC) tạo với (SBC) một góc $\phi$ thỏa mãn $\cos \phi =\frac{\sqrt{2}}{4}$ . Gọi $\alpha$ là góc tạo bởi SA và mặt phẳng (ABC). Tính $\tan \alpha$

Cho phương trình ${\log }_3^{2}x-{\log }_{3}x+m-3=0$ . Tìm tất cả các giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt $x_1 < x_2$ thỏa mãn $x_2 – 81x_1 < 0$

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.

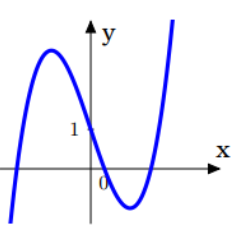
Hỏi hàm số đó là hàm số nào?

Cho mặt phẳng (Q): x - y + 2z - 2 = 0. Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q), đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho $MN=2\sqrt{2}$ .

Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).

Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy hai điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng $R^2\sqrt{2}$ , thể tích hình nón đã cho bằng

Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).

Tập xác định của hàm số $y={\log }_2\left(x^2-2x\right)$  là

Cho các đường thẳng $d_1:\frac{x-1}{1}=\frac{y+1}{2}=\frac{z}{-1}$  và $d_2:\frac{x-2}{1}=\frac{y}{2}=\frac{z+3}{2}$  . Viết phương trình đường thẳng $∆$ đi qua A (1; 0; 2), cắt $d_1$ và vuông góc với $d_2$.

Cho hàm số y = f (x) có đồ thị (C), biết tiếp tuyến của đồ thị (C) tại điểm có hoành độ

x = 0 là đường thẳng y = 3x - 3. Giá trị của $\underset{x\to 0}{\lim }\frac{3x}{f\left(3x\right)-5f\left(4x\right)+4f\left(7x\right)}$

Cho hàm số $y = x^4 - 2m{x}^2 + 3m - 2$ (với m là tham số). Có bao nhiêu giá trị của tham số m để các điểm cực trị của đồ thị hàm số đều nằm trên các trục tọa độ?

Tích tất cả các nghiệm của phương trình $3^{x^2-2}=5^{x+1}$  là

Phương trình ${\log }_3\frac{2x-1}{{\left(x-1\right)}^2}=3x^2-8x+5$ có hai nghiệm là a và $\frac{a}{b}$  (với a,b Î N* và  là phân số tối giản). Giá trị của b là

Trong hệ tọa độ Oxyz, cho đường thẳng $d:\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z+2}{3}$ . Phương trình nào sau đây là phương trình tham số của d?

Phương trình $z^2 + 2z + 10 = 0$ có hai nghiệm là $z_1, z_2$. Giá trị của $\left|z_1-z_2\right|$ là

Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.