Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải

*Phương pháp giải:
Áp dụng công thức lượng giác cơ bản
*Lý thuyết:
1. Công thức lượng giác cơ bản
2. Công thức cộng lượng giác
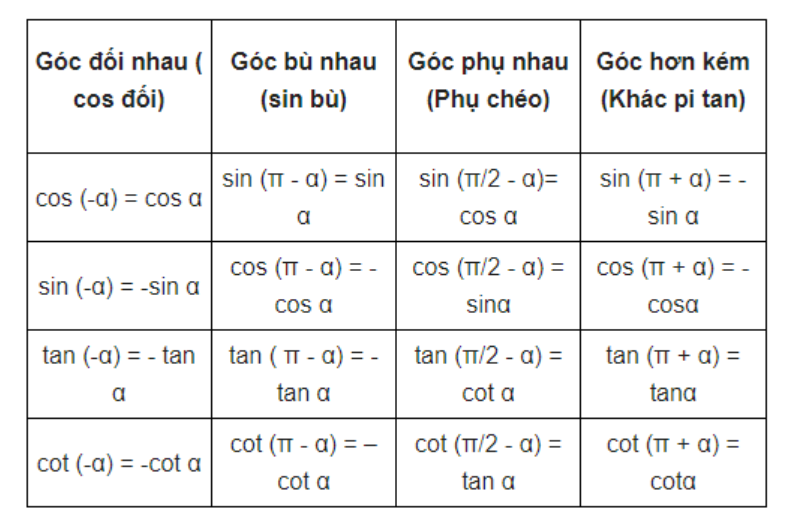
3. Công thức các cung liên kết trên đường tròn lượng giác
Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π
Cung hơn kém
+ cos( + x) = - sinx
+ sin( + x) = cosx
Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Bài 2: Cho Hình 23.
a) Chứng tỏ rằng m //n.
b) Chứng tỏ rằng AB vuông góc N

Câu 3:
Cho tứ diện SABC. Gọi I, H lần lượt là trung điểm của SA, AB. Trên SC lấy điểm K sao cho CK=3KS
a) Tìm giao điểm của BC VÀ IHK
b) GọI M là trung điểm của IH. tìm giao điểm KM với ABC
Câu 5:
Cho tứ diện ABCD. Gọi M, N, P là ba điểm lần lượt nằm trên ba cạnh AB, CD, AD. Tìm giao tuyến của các cặp mặt phẳng:
a. (ABN) và (CDM).
b. (ABN) và (BCP)
Câu 13:
Cho biết số Un biết Un = căn 3 cosn - sinn. Dãy số Un bị chặn dưới và bị chặn trên lần lượt bởi các số m và M nào dưới đây
Câu 15:
Cho góc tù xOy. Trong góc xOy, vẽ Ot vuông góc với Ox và Ov vuông góc với Oy.
a) Chứng minh
b) Chứng minh hai góc xOy và tOv bù nhau.
c) Gọi Om là tia phân giác của góc xOy. Chứng minh Om là tia phân giác của góc tOv.




