Câu hỏi:
23/07/2024 108
Cho các số thực a, b > 1 và phương trình có hai nghiệm phân biệt m, n. Giá trị nhỏ nhất của biểu thức bằng:
Cho các số thực a, b > 1 và phương trình có hai nghiệm phân biệt m, n. Giá trị nhỏ nhất của biểu thức bằng:
A. 200
B. 174
C. 404
D. 400
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Từ giả thiết đưa về phương trình bậc hai ẩn lnx.
- Sử dụng định lí Vi-ét cho phương trình bậc hai tìm tích abmn.
- Tìm GTNN của biểu thức P nhờ BĐT Cô-si.
Cách giải:
Theo bài ra ta có:
Đặt t = lnx phương trình trở thành
Vì phương trình (*) có 2 nghiệm phân biệt nên
Phương trình ban đầu có 2 nghiệm phân biệt m, n nên phương trình (*) có 2 nghiệm phân biệt
Khi đó áp dụng định lí Vi-ét ta có
Do
Xét ta có
Dấu “=” xảy ra
Vậy
Chọn D.
Phương pháp:
- Từ giả thiết đưa về phương trình bậc hai ẩn lnx.
- Sử dụng định lí Vi-ét cho phương trình bậc hai tìm tích abmn.
- Tìm GTNN của biểu thức P nhờ BĐT Cô-si.
Cách giải:
Theo bài ra ta có:
Đặt t = lnx phương trình trở thành
Vì phương trình (*) có 2 nghiệm phân biệt nên
Phương trình ban đầu có 2 nghiệm phân biệt m, n nên phương trình (*) có 2 nghiệm phân biệt
Khi đó áp dụng định lí Vi-ét ta có
Do
Xét ta có
Dấu “=” xảy ra
Vậy
Chọn D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho tập hợp Từ tập hợp A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao cho các số này lẻ và không chia hết cho 5?
Cho tập hợp Từ tập hợp A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao cho các số này lẻ và không chia hết cho 5?
Câu 4:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và có thể tích bằng Tính chiều cao h của khối chóp đã cho.
Câu 6:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng và . Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng và . Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
Câu 8:
Cho hàm số y = f(x) có bảng biến thiên như sau:
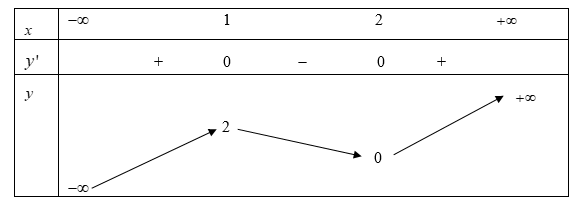
Số nghiệm thực của phương trình là
Cho hàm số y = f(x) có bảng biến thiên như sau:

Số nghiệm thực của phương trình là
Câu 10:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình Tính diện tích mặt cầu (S)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình Tính diện tích mặt cầu (S)
Câu 11:
Cho hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số là:
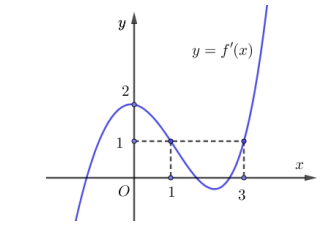
Câu 13:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác ABC đều và có độ dài đường cao là Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác ABC đều và có độ dài đường cao là Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng:
Câu 14:
Cho hàm số y = f(x) xác định trên và có đạo hàm trong đó . Hàm số đồng biến trên khoảng nào?
Cho hàm số y = f(x) xác định trên và có đạo hàm trong đó . Hàm số đồng biến trên khoảng nào?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)