Câu hỏi:
20/07/2024 133
Cho A là một điểm tùy ý nằm trên đường trung trực của đoạn thẳng BC sao cho A không thuộc BC. Khẳng định nào dưới đây là đúng?
a) AB = AC.
b) Tam giác ABC đều.
c) \(\widehat {ABC} = \widehat {ACB}\).
d) Tam giác ABC cân tại đỉnh A.
a) AB = AC.
b) Tam giác ABC đều.
c) \(\widehat {ABC} = \widehat {ACB}\).
d) Tam giác ABC cân tại đỉnh A.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
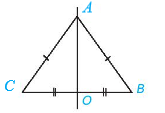
Điểm A thuộc đường trung trực của BC nên AB = AC (điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó).
Do đó, ∆ABC cân tại đỉnh A.
Suy ra \(\widehat {ABC} = \widehat {ACB}\).
Vậy các câu a), c), d) đúng.
Câu b) chưa đúng vì ta chưa đủ dữ kiện để tam giác ABC đều, do ta chỉ có AB = AC, và độ dài đoạn thẳng BC bất kì.
Hướng dẫn giải

Điểm A thuộc đường trung trực của BC nên AB = AC (điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó).
Do đó, ∆ABC cân tại đỉnh A.
Suy ra \(\widehat {ABC} = \widehat {ACB}\).
Vậy các câu a), c), d) đúng.
Câu b) chưa đúng vì ta chưa đủ dữ kiện để tam giác ABC đều, do ta chỉ có AB = AC, và độ dài đoạn thẳng BC bất kì.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:
Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).
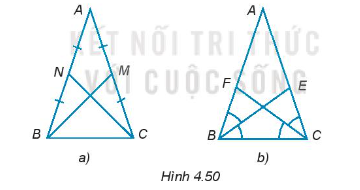
Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:
Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).

Câu 2:
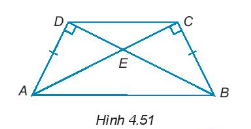
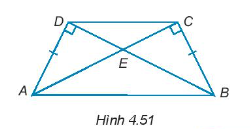
Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:
∆AEB và ∆DEC là các tam giác cân đỉnh E.
Câu 3:
Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:
Hai đường phân giác BE, CF bằng nhau (H.4.50b).
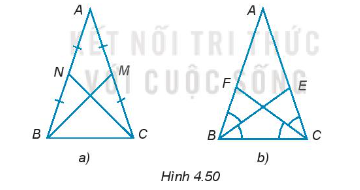
Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:
Hai đường phân giác BE, CF bằng nhau (H.4.50b).

Câu 4:
Cho tam giác ABH vuông tại đỉnh H có \(\widehat {ABH} = 60^\circ \). Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = \(\frac{{AB}}{2}\).
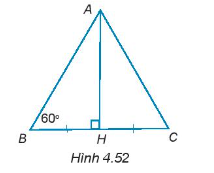
Cho tam giác ABH vuông tại đỉnh H có \(\widehat {ABH} = 60^\circ \). Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = \(\frac{{AB}}{2}\).

Câu 5:
Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:
AB // CD.
Câu 6:
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
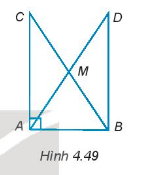
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.

Câu 7:
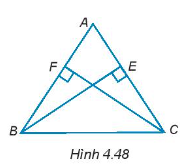
Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.

Câu 8:
Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?
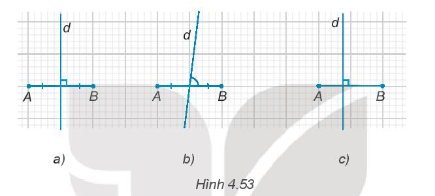
Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?

Câu 9:
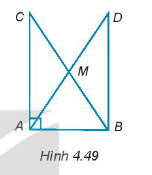
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD = ∆BAC.
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD = ∆BAC.

Câu 10:
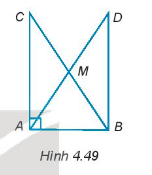
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD vuông tại B.
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD vuông tại B.

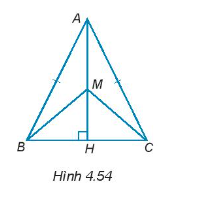
Câu 11:
Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường thẳng AH sao cho M không trùng với A (H.4.54). Chứng minh rằng: \(\widehat {MBA} = \widehat {MCA}\).

Câu 12:
Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?
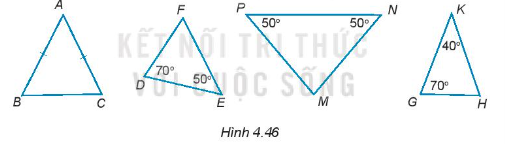
Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?

Câu 13:
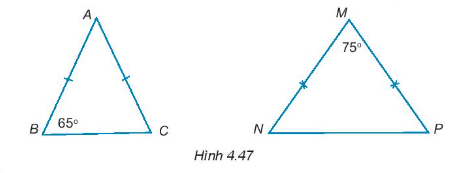
Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).